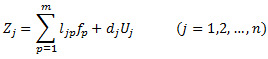СОВЕРШЕНСТВОВАНИЕ МЕТОДОЛОГИИ ОЦЕНКИ КАЧЕСТВА ЗЕРНА

Даулетбаков Б. ¹, Маукебаева Р.М. ²

¹Доктор экономических наук, профессор, ²Старший преподаватель Алматинский технологический университет

Работа выполнена при поддержке гранта «Лучший преподаватель вуза» 2014 года

СОВЕРШЕНСТВОВАНИЕ МЕТОДОЛОГИИ ОЦЕНКИ КАЧЕСТВА ЗЕРНА

Аннотация

В статье рассмотрено - оценка потенциальных свойств зерна; анализ технологических схем, параметров и выбор минимального количества параметров, в комплексной форме учитывающих влияние физико-химических структурно-механических и биологических свойств перерабатываемого зерна на основе факторного анализа.

Ключевые слова: технологический цикл, оценки, мельничное производство, факторный анализ.

Dauletbakov B.¹, Maukebaeva R.M.²

¹Doctor of Economics, professor, ²Senior Lecturer, Almaty Technological University

This work was supported by the grant «The best teacher of high school» in 2014

IMPROVEMENT OF THE METHODOLOGY FOR GRAIN QUALITY ASSESSMENT

Abstract

In the article - assessment of the potential properties of the grain; analysis of technological schemes, options, and select the minimum number of parameters to take into account the effect of the complex form of physical and chemical structural, mechanical and biological properties of the processed grain on the basis of factor analysis.

Keywords: technological cycle assessment, mill production, factor analysis.

Введение

В технике и технологии мельничного производства актуальными остаются следующие задачи: оценка потенциальных свойств зерна; анализ технологических схем, параметров и выбор минимального количества параметров, в комплексной форме учитывающих влияние физико-химических структурно-механических и биологических свойств перерабатываемого зерна.

В последние годы в Казахстане[1,2] и странах ближнего зарубежья [3-6] уделяется большое внимание научным разработкам по качеству муки в зависимости от её использования в пищевом секторе экономики.

За рубежом применяется дифференцированный подход к качеству муки в зависимости от её использования [7-10]. Так, например, в Великобритании для оценки технологических достоинств зерна пшеницы пользуются следующими показателями: число падения, измеряемое методом Хагберга-Пертена, тест на содержание белка, большое внимание уделяется такому показателю, как сорт пшеницы [7].

Основная цель

В настоящее время в Казахстане основном контроль хлебопекарных свойств зерна проводится на конечной стадии её переработки, когда уже затрачены значительные средства и усилия на получение готового продукта и остаётся мало возможностей влиять на его качество. В связи с этим важной задачей является переход от контроля качества готовой продукции к предварительному контролю на стадии её производства – по всему технологическому циклу – «показатель зерна – мука – теста – хлеб», позволяющему существенно снизить затраты на проведение исследований и прогнозировать качество конечного продукта, а также регулировать свойства промежуточных продуктов в нужном направлении.

В рамках по такому технологическому циклу введения агрегированных комплексных показателей до сих пор нигде не ставилась. В связи с этим актуальной задачей является совершенствование методологии оценки качества зерна.

Такая постановка задачи может быть решена на основе факторного анализа, который позволяет при известных числовых значениях рассматриваемых показателей определить количество стоящих за ними скрытых факторов, каждый из которых получает определенную содержательную характеристику, обусловленную его отношениями с рассматриваемыми показателями. Распределение показателей качества зерна по факторам позволяет резко сократить количество переменных, рассматриваемых в задачах о зерне.

Целью факторного анализа как ветви математической статистики, является разработка моделей и методов, позволяющих анализировать и интерпретировать массивы экспериментальных или наблюденных данных вне зависимости от их физической природы [11-13].

Массив исследуемой информации представляет собой прямоугольную матрицу ||X_ij||, строки которой характеризуют n объектов наблюдений (i=1,2,…,n), а столбцы – набор признаков, описывающих эти наблюдения (j=1,2,3,…,m).

При практическом исследовании размеры матрицы обычно достаточно большие. Число строк может колебаться от нескольких десятков до нескольких тысяч, а число столбцов от одного-двух до нескольких десятков. Поэтому непосредственный анализ матриц невозможен. Для оценки таких матриц в математической статистике возникло много методов, которые предназначены для того, чтобы «сжать» исходную информацию, заключенную в матрице, извлечь из информации наиболее «существенное».

В настоящее время имеется несколько методов решения задач оценок связи между параметрами. Наиболее простым и пригодными для использования являются корреляционный, регрессионный и факторный анализы. Корреляционный и регрессионный анализы целесообразно использовать для раскрытия причинно-следственных связей. Факторный анализ оценивает связь группы наблюдаемых параметров с заранее неизвестными не наблюдаемыми (факторами и дает уравнения, определяющие эти факторы).

Другими словами, Факторный анализ может рассматриваться как расширение корреляционного анализа. Его выгодно использовать всякий paз, когда большое число переменных должно быть проверено на взаимозависимость. В этом процессе задача размерности (m m) преобразуется в задачу размерности (n m) где n£m. Цель состоит в том, чтобы ограничить влияние переменных только несколькими факторами.

Существует множество прекрасных книг по факторному анализу. Более подробное описание приводят Лоули Д., Максвелл А. [11], Харман Г [12], Жуковская В.М. и Мучник И.Б. [13].

Типичные задачи факторного анализа

В прикладных исследованиях с использованием факторного анализа встречаются разнообразные постановки задач. Различия состоят как в самом подходе (в общей установке исследователя, применяющего факторные модели), так и в формулировке цели, в организации исходного материала, в использовании полученных результатов. Все эти различия определяют выбор модели и решение ряда вопросов, связанных с формализацией задачи.

Задачи типологии.

Весьма часто исследователь сталкивается с необходимостью подразделить множество наблюдаемых им объектов или явлений, описанных неким набором признаков, на максимально однородные (по этим признакам) группы. Ценность такой группировки состоит в том, что для полученных групп часто оказывается возможным построение достаточно простых моделей функциональных связей.

Допустим необходимо оптимизировать производственную деятельность большого числа предприятий [14]. В этом случае необходимо разработать типологию предприятий, т.е. разбить все предприятия на группы максимально однородные по условиям производства, а затем строить программы для предприятий, составляющих каждую группу.

Схему решения задачи типологии с использованием факторного анализа можно представить в виде последовательного преобразования следующих матриц: исходных данных, парных корреляций, факторных нагрузок, факторных весов, расстояний между объектами по отдельным факторам.

На основании последней матрицы строится таксономия; после введения дополнительных ограничений осуществляется обоснование и интерпретация типологии. Таким образом, типология строится на основе результатов факторного анализа, исходя из значений факторных весов. В тех случаях, когда признается, что для построения таксономии достаточно учесть два или три первых фактора, выявление типов объектов может быть осуществлено экспертным путем с помощью визуального анализа (анализа гистограмм весов по отдельным факторам), в других случаях необходимо использование алгоритмов автоматической классификации [15].

Задача анализа системы признаков.

При анализе системы признаков мы сталкиваемся не с классификацией объектов, а с классификацией показателей.

Пусть мы имеем n наблюдений (i=1,2,…,n), о сочетаниях m признаков (j=1,2,3,…,m) качества X_ij. Требуется разбита пространство признаков на максимально взаимосвязанные группы. Это типичная задача построения классификации, заключающаяся в целенаправленном упорядочении исходной информации, в разделении множества признаков на соподчиненные и зависимые.

Допустим, имеется m признаков качества зерна и муки. В рамках данной задачи возможно:

• минимизировать систему показателей качества зерна, с заданной степенью точности, описывающих состояние зерновой массы. Это возможно путем конструирования новых обобщающих характеристик, подлежащих интерпретации. В работе [5] 11 показателей качества были сведены к двум факторам: белково-протеиназному и фактору стекловидности.

Задача районирования.

В практике планирования экономического развития часто встает задача деления территории на максимально однородные по ряду показателей области. В этом случае объектами могут служить различные территориальные единицы (районы, области, республики и т.д.). То или иное объединение территориальных единиц дает схему районирования изучаемой территории [13, 16-22].

Основные этапы исследования

Постановка задачи. Одной из основных предпосылок разработки и совершенствования методологии оценки качества зерна является: оценка потенциальных свойств зерна; анализ технологических схем, параметров и выбор минимального количества параметров, в комплексной форме учитывающих влияние физико-химических структурно-механических и биологических свойств перерабатываемого зерна.

Матрица данных. Для выявления основных закономерностей связи нами исследовалось качество зерна, муки, теста и хлеба образцов пшеницы сорта Саратовская 29 по областям Северного Казахстана, расположенным рядом с хлебоприемными предприятиями.

При этом для изучения качества зерна рассматривались:

1) Влажность, %; 2) Сорная примесь, %; 3) Зерновая примесь, % ; 4) Натура г/л, 5) Общая стекловидность, %; 6) Полная стекловидность, %; 7) Зольность, %; 8) Белок, %; 9) Клейковина, %; 10) Клопом-черепашкой, %.

Для качества муки рассматривались:

11) Клейковина, %; 12) Зольность, %.

Для качества теста рассматривались показатели приборов альвеографа и фариографа

13) Упругость, P; 14) Растяжимость, L; 15) Отношение P/L; 16) Удельная работа на деформацию теста; 17) Водопоглотительная способность, %; 18) Время образования теста; 19) Устойчивость теста; 20) Разжижжение теста; 21) Показатель волорометра.

Для качества хлеба рассматривались:

22) Объемный выход хлеба; 23) Расплываемость хлеба V/D.

Значения показателей оцениваются для каждого из 70 опытов, представляющих генеральную совокупность в целом. Таким образом, матрица данных имеет размерность 70´23. Строки ее соответствуют 70 опытам, столбцы - 23 показателям. Каждый элемент матрицы есть значение одного из 23 показателей для одного из 70 опытов.

Предварительные преобразования данных.

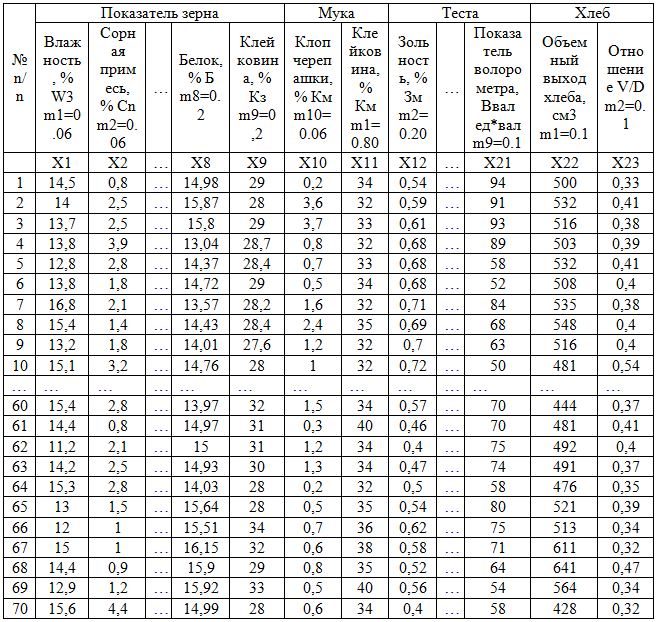
Для приведения всех показателей к единому масштабу использовано преобразование исходных чисел к рангам, т. е. каждый столбец матрицы исходных данных представлен набором порядковых номеров (от 1 до 70) в соответствии с порядковыми местами опытов по значениям данного показателя (таблица 1).

Таблица 1 – Качество зерна пшеницы

Процедура факторного анализа проводится с помощью пакета прикладных программ «STATISTICA 10» c использованием метода главных компонент [14].

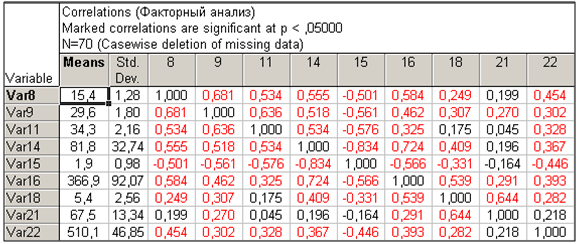
Матрица корреляций. На основе матрицы порядковых номеров рассчитана матрица парных корреляций между показателями (рисунок 1).

Рисунок 1 – Матрица корреляций

Матрица коэффициентов корреляции (рисунок 1) служит количественным выражением степени связи между каждой парой из рассматриваемых 23 показателей. Анализ корреляционной матрицы позволяет выделить наиболее тесно взаимосвязанные пары показателей; это показатели 8 и 9,9 и 6, 11 и 9, 14 и 16, 15 и 14,16 и 14, 18 и 21, 22 и 8. Структура взаимосвязей между группами показателей выявляется с помощью факторного анализа.

Вычисление корреляционной матрицы –  первый  этап факторного анализа.

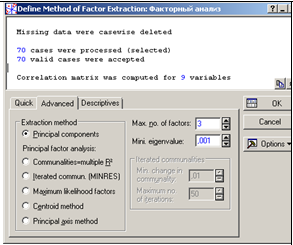
После щелчка по Ok можно перейти к следующему диалоговому окну. Define Method of Factor Extraction (Определить метод выделения факторов) (рисунок 2).

Рис. 2

Рис. 3

Выбираем опцию Principal  components (Главные  компоненты) и щелкнем по кнопке OK.

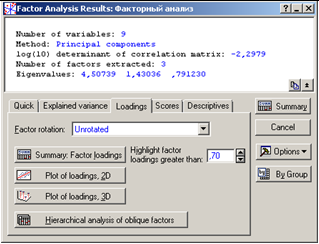
Система быстро произведет вычисления, и на экране появится окно Factor Analysis Results (Результаты факторного анализа) (рисунок 3).

В верхней части окна Результаты факторного анализа дается информационное сообщение:

Number of variables (число анализируемых переменных) – 9;

Method (метод анализа) – главные компоненты;

log(10) determination of correlation matrix(десятичный логарифм детерминанта корреляционной матрицы) –  -2,2979;

Number of Factor extraction (число выделенных факторов) – 3;

Eigenvalues (собственные значения) – 4,50739; 1,43036; 0,791230.

В нижней части окна находятся подразделы, позволяющие всесторонне просмотреть результаты анализа численно и графически.

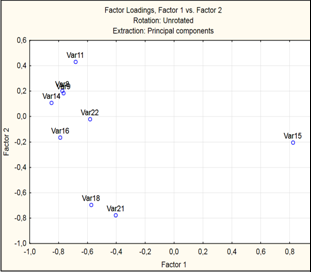
Plot of loadings, 2D и Plot of loadings, 3D (Графики  нагрузок) – эти опции  построят графики факторных нагрузок в проекции на плоскость любых двух выбранных факторов (рисунок 4) и в проекции в пространство трех выбранных факторов (для чего необходимо наличие как минимум трех выделенных факторов).

Рис. 4

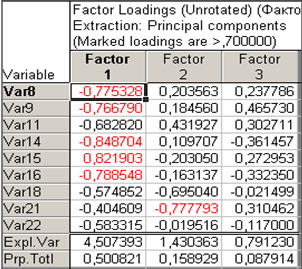
Рис. 5

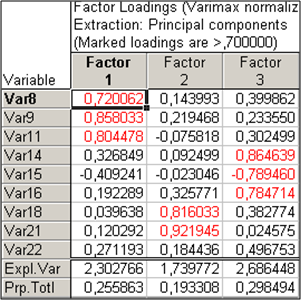
Summary. Factor  loadings (Факторные нагрузки). Эта  опция вызывает таблицу с текущими факторными нагрузками (рисунок 5), т.е. вычисленными для данного метода вращения факторов, который указан справа от соответствующей кнопки.

В этой таблице факторам соответствуют столбцы, а переменным – строки и для каждого фактора указывается нагрузка каждой исходной переменной, показывающая относительную величину проекции переменной на факторную координатную ось. Факторные нагрузки могут интерпретироваться как корреляции между соответствующими переменными и факторами – чем выше нагрузка по модулю, тем больше близость фактора к исходной переменной; т.о., они представляют наиболее важную информацию для интерпретации полученных факторов. В сгенерированной таблице для облегчения трактовки будут выделены факторные нагрузки по абсолютной величине больше 0,7.

По-видимому, первый фактор более коррелирует с переменными, чем второй.

Их трудно проинтерпретировать, возникает вопрос, какой смысл придать второму фактору. В этом случае целесообразно прибегнуть к повороту осей, надеясь получить решение, которое можно интерпретировать в предметной области.

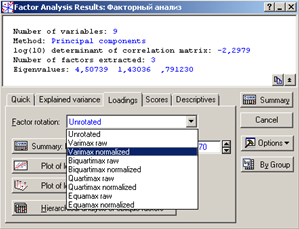
Щелкнем по меню Factor rotation (Вращение факторов) (рисунок 6).

Цель вращения – получение простой структуры, при которой большинство наблюдений находится вблизи осей координат. При случайной конфигурации наблюдений невозможно получить простую структуру.

Рис. 6

Рис. 7

В данном раскрывающемся меню мы можем выбрать различные повороты оси. Окно предлагает несколько возможностей оценить и найти нужный поворот следующими методами: Varimax – Варимакс; Biquartimax – Биквартимакс; Quartimax – Квартимакс; Equamax – Эквимакс.

Дополнительный термин в названии методов – normalized (нормализованные) – указывает на то, что факторные нагрузки в процедуре нормализуются, т.е. делятся на корень квадратный из соответствующей дисперсии. Термин raw (исходные) показывает, что вращаемые нагрузки не нормализованы.

Нажимаем кнопку Varimax normalized (Варимакс нормализованный).

Система произведет вращение факторов методом нормализованного варимакса, и окно Factor Analysis Results (Результаты факторного анализа) снова появится на мониторе.

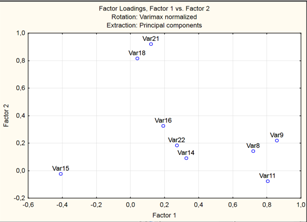
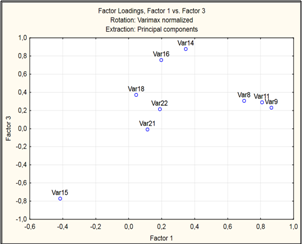
Вновь нажимаем в этом окне кнопку Plot of Loadings 2D (Двумерный график нагрузок). Мы опять увидим график нагрузок (рисунок 7).

Конечно, этот график немного отличается от предыдущего. Посмотрим еще нагрузки численно, инициировав кнопку Факторные нагрузки (Factor loadings). Щелкнем на кнопке Summary. Factor loadings, вы откроете окно (рисунок 8):

Рис. 8

Рис. 9

Теперь найденное решение уже можно интерпретировать. Факторы чаще интерпретируют по нагрузкам. Первый фактор теснее всего связан с X8 , X9, X11.

Второй фактор – X18 и X21.

Третий фактор – X14, X15, X16.

Таким образом, произвели классификацию переменных на три группы. Возникает вопрос: сколькими же факторами следует ограничиваться на практике?

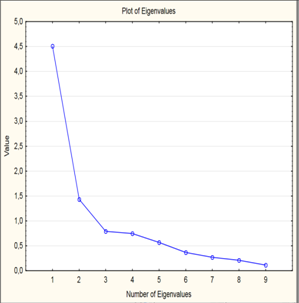
Для этого в программном пакете STATISTICA существует критерий Scree plot (Критерий каменистой осыпи). В окне Factor Analysis Results нажимаем кнопку Scree plot получаем следующий график собственных значений (рисунок 9):

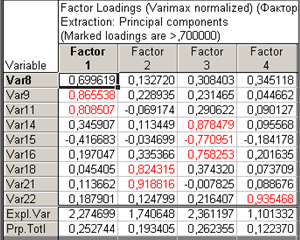
В точках с координатами 1, 2, 3, 4 осыпание замедляется наиболее существенно, следовательно, теоретически можно ограничиваться четырьмя факторами (рисунок 10):

Рис. 10

Рис. 11

Найденное решение можно интерпретировать. Факторы чаще интерпретируют по нагрузкам. Первый фактор теснее всего связан с X9, X11.

Второй фактор – X18 и X21.

Третий фактор – X14, X15, X16.

Четвертый фактор – X22.

Таким образом, произвели классификацию переменных на четыре группы.

Вновь нажимаем в этом окне кнопку Plot of Loadings 2D (Двумерный график нагрузок). Мы опять увидим график нагрузок (рисунок 11).

Преобразование корреляционной матрицы (рисунок 1) в матрицу факторных нагрузок (Рисунок 5, Рисунок 8 и Рисунок 10) было осуществлено нами несколькими способами: с помощью центроидного метода, метод минимальных остатков, метод максимального правдоподобия и метода главных компонент. Сопоставление результатов подтверждает вывод об объективном характере - выявленной факторной структуры: при всех четырех способах расчета матрицы факторных нагрузок оказались весьма близкими, что подтверждает предложенную интерпретацию с помощью метода главных компонент.

В строке Expl.Var (рисунок 5) приведена дисперсия, приходящаяся на тот или иной фактор. В строке Prp.Totl приведена доля дисперсии, приходящаяся на первый, второй и третий факторы. Вклад каждого фактора в общую изменчивость 50,1%, 15,9% и 8,8% соответственно.

Представленная в рисунке 5 матрица факторных нагрузок получена с помощью метода главных компонент. Основой для определения факторов послужил последовательный ряд собственных значений исходной корреляционной матрицы. Вклад каждого из факторов в суммарную дисперсию сопоставлялся с некоторым порогом; на этой основе факторизация прекращена после извлечения четырех факторов (рисунок 5).

Все показатели качества зерна, поскольку они характеризуют одно и то же материальное тело (данную партию зерна), так или иначе взаимно связаны. Часть из них связана между собой более тесно, в результате изменения одного из них с наибольшей вероятностью вызывает изменение другого. Связь между показателями другой их части выражена слабее или же полностью отсутствует. Это позволяет, опираясь на общую и частную дисперсию, из отобранных для анализа 23 показателей качества выбрать несколько обобщенных факторов (групп показателей качества), изменение которых влечет за собой существенное изменение других показателей качества. В нашем случае такими обобщенными факторами являются четыре, обозначенные нами Factor 1 - f₁, Factor 2 - f₂, Factor 3 - f₃ и Factor 4 - f₄.

Полученное факторное решение в терминах двух факторов можно рассматривать как некоторое промежуточное решение, удовлетворяющее основной факторной теореме:

где Z_j  - нормированное значение  j-того показателя;

 f_p - p-й общий фактор с дисперсией, равной единице;

U_j - характерный фактор, учитывающий остаточную дисперсию;

l_jp, d_j - факторная нагрузка  j-того показателя на  p-й общий

фактор.

Ошибки измерения выступают как специфические факторы (U_j) и в дальнейшем специально не учитываются.

С помощью вращения системы координат получается бесконечное множество решений, адекватно описывающих процесс. Конфигурация точек в пространстве общих факторов и расстояние от начала координат не изменяются.

На рисунки 4, 7 и 11 приведены результаты вращения системы координат для пшеницы.

По оси абсцисс отложены нагрузки на первый фактор, по оси ординат - на второй. В пространстве факторов показатели качества изображаются векторами, квадраты модулей которых равны факторным дисперсиям.

Согласно основному принципу факторного анализа, векторы должны образовывать пучки. Разброс векторов относительно центра пучка характеризует неопределенность при замене пучка векторов-признаков фактором. На рисунке 11 четко видно наличие четырех пучков. Первый из них включает показатели: количество клейковины зерна и муки. Второй - время образования теста и показатель волорометра. Третий - растяжимость, отношение P/L; удельная работа на деформацию теста и время образования теста. Четвертый - объемный выход хлеба.

Первый фактор, следовательно, можно интерпретировать как фактор показателя зерна, второй - показателя муки, третий - показателя теста и четвертый - показателя хлеба.

Показатели натура, разжижение теста, клопчерепашки, зольность является самостоятельным признаком, не зависящим от показателей, образующих пучки f₁, f₂, f₃ и f₄. Он оценивает зерно с мукомольной точки зрения (выходы сортовой муки).

Таким образом, для оценки качества зерна необходимо учитывать конкретные показатели. В связи с этим перед нами стоит задача разработать основы комплексной системы оценки качества зерна, учитывающей целевое назначение зерна и зернопродуктов, с использованием современных методов анализа, повышающих достоверность обеспечения адекватности потребительских свойств сырья требованиям пищевой и перерабатывающей промышленности.

В ходе нашей работы, на стадии производства с использованием факторного анализа разработан показатель оценки качества зерна по всему технологическому циклу:

• «показатель зерна – мука – теста – хлеб», позволяющему существенно снизить затраты на проведение исследований и прогнозировать качество конечного продукта, а также регулировать свойства промежуточных продуктов в нужном направлении;
• выявлены значимые показатели качества зерна;
• составлены примерные классификации показателей оценки качества зерна.

Выведенная нами система факторов: «показатель зерна – мука – теста – хлеб», показывает, что каждый из этих параметров находит свое максимальное выражение посредством разных факторов.

Выводы

1. Метод факторного анализа позволяет перейти от большого количества показателей качества зерна к ограниченному числу комплексных факторов, определяющих связь между этими показателями и их технологическое значение.
2. Достоинство метода - возможность выявления связей между изучаемыми показателями качества зерна, не вскрываемых методами корреляционного анализа и уравнений регрессии.
3. Технологическое достоинство зерна - пшеницы, идентично описываясь в факторном пространстве, образует систему четырех факторов: «показатель зерна – мука – теста – хлеб».
4. Показатель зольности однозначно через факторы не выражается, поскольку он характеризует лишь одну сторону мукомольного производства (выход муки) и непосредственно не связан с хлебопекарным достоинством зерна и муки.

Литература

1. Казахстан: безотходные технологии переработки зерновых культур / newsland. com/news/detail/id/693657/.
2. Современные аспекты научно-технологического обеспечения переработки сельскохозяйственного сырья и отходов: Сб. докладов международной научно-практической конференции, 9-10 октября 2014 г. – Астана, 2014.
3. Торжинская Л.Р.,  Роменский  Н.В.,  Атанас  Л.Г.,  Умлева   Н. Г. Изв.  вузов  СССР,  Пищевая  технология,  №2, 12,
4. Сердюков П.И.  Мукомольные  признаки  качества   пшеницы   и   их  значимость для мукомольного производства.  ЦНИИТЭИ Минзага  СССР, М.,
5. Казакова И. Е. Моделирование технологического качества зерна методом факторного анализа. Известия вузов СССР, Пищевая технология, № 3, 88, 1975.
6. ГОСТ Р 52189-2003. Мука пшеничная. Общие технические условия. – Введ. 2003-29-12. – М. : Изд-во стандартов, 2004. – III, 8 с.
7. Бутковский В.А., Касатов Д.А. Мукомольная промышленность Великобритании. // Хлебопродукты. №12. - 2003. - с. 14-16.
8. Landi. Garatteristiche ottimali del grano duro e tenero per I produtti destinati aii'alimentazione umana. // Informatore agrario. 1987. - т.43. - №36. - s. 29-31.
9. Tiefenbacher, M.Dobrovics. Mehle tur die Waffeiherstellung. // Ver-offentl.Arbeitsgemensch.Getreideferschung e.v. 2000. - Bd.285. - s. 65-73.
10. Roy Chung Kah Hee. Слабая мука для сильного печенья / Roy Chung Kah Hee // Flour – Food for Life: материалы 2nd International Muhlenchemie Symposium, 17/18 June 2004, Hamburg.
11. Лоули Д., Максвелл А. Факторный анализ как статистический метод (Пер. с англ.). «Мир»,
12. Xарман Г. Современный факторный анализ (Пер. с англ.). М., «Статистика», 1972.
13. Жуковская В.М. и Мучник И.Б. Факторный анализ в социально-экономических исследованиях. М., «Статистика», 1976.
14. Жуковская В.М., Кудина И.М. Типологическое изучение сельского хозяйства США и Канады с использованием многофакторного анализа. Сб. Вопросы экономической и политической географии зарубежных стран. М., 1971.
15. Браверман Э. М., Дорофеюк А. А., Лумельский В. Я., Мучник И. Б. Диагонализация матриц связи и выявление скрытых факторов.— В сб.: Труды Института проблем управления. М., «Наука», 1971, вып. I.
16. Berry B. Inductive Approach to the Regionalization of Economic Development — «Research Paper of the Univ. of Chicago Dep-t of Geography», 1960, №62.
17. Economic Regionalization and numerical methods. Eds: Berry R., Wrobel A. In: «Geographia Polonica». Warzawa, 1968, vol. 15.
18. Edwards C. Regional Variations in Economic Growth with Emphasis on Rural Areas. — «Agricultural Economic Report», Wash., 1971, № 205.
19. Gould P. R. Problems of Space Preference Measures and Relationships. - «Geographical Analyses», 1969, vol. 1, № 1.
20. Даулетбаков Б, Изтаев А.И., Арынгазин К.Ш., Омаоров Т.Е., Сырлыбаева Л.М. Моделирование качества зерна с применением факторного анализа. Пищевая технология и сервис. Алматы, 2007. №2. С. 3-7.
21. Изтаев А. Технологические качества зерна пшеницы Казахстана. – Алма-Ата: Кайнар, 1992, 368 с.
22. Казаков Е.Д. Зерноведение с основами растениеводства. «Колос», М., 1973.
23. http://www.statsoft.com/

References

1. Kazakhstan: non-waste technology for processing of crops / newsland. com / news / detail / id / 693657 /.
2. Modern aspects of scientific and technological support processing of agricultural raw materials and waste: Sat. the reports of the international scientific-practical conference on 9-10 October 2014 - Astana, 2014.
3. Torzhinskaya LR, Romenskii NV, Atanas LG, NG Umleva Math. universities of the USSR, Food technology, №2, 12, 1965.
4. Serdyukov PI Flour signs of quality wheat and their importance for the production of flour. TSNIITEI mine layer of the USSR, Moscow, 1970.
5. Kazakova IE Modeling technological quality of grain by factor analysis. Proceedings of the universities of the USSR, Food technology, № 3, 88, 1975.
6. GOST R 52189-2003. Wheat flour. General specifications. - Enter. 2003-29-12. - Moscow: Publishing House of Standards, 2004. - III, 8.
7. Butkovskiy VA, touching DA UK milling industry. // Bakery. №12. - 2003. - with. 14-16.
8. A.Landi. Garatteristiche ottimali del grano duro e tenero per I produtti destinati aii'alimentazione umana. // Informatore agrario. 1987 - t.43. - №36. - S. 29-31.
9. K.Tiefenbacher, M.Dobrovics. Mehle tur die Waffeiherstellung. // Ver-offentl.Arbeitsgemensch.Getreideferschung ev 2000. - Bd.285. - S. 65-73.
10. Roy Chung Kah Hee. Weak to strong flour pastry / Roy Chung Kah Hee // Flour - Food for Life: Materials 2nd International Muhlenchemie Symposium, 17/18 June 2004, Hamburg.
11. D. Lawley, Maxwell A. Factor analysis as a statistical method (trans. From English.). "Peace", 1967.
12. Xarman G. Modern factor analysis (Per. From English.). Moscow, "Statistics", 1972.
13. VM Zhukovska and IB Muchnik Factor analysis of the socio-economic research. Moscow, "Statistics", 1976.
14. Zhukovska VM Kudina IM Typological study of US agriculture and Canada, using multivariate analysis. Coll. Issues of economic and political geography of the foreign countries. M., 1971.
15. EM Braverman, Dorofeyuk AA Lumelskii VY, Muchnik IB Diagonalization of matrices of communication and identify hidden in faktorov.- Sat .: Proceedings of the Institute of management problems. "Nauka", 1971, vol. I.
16. Berry B. Inductive Approach to the Regionalization of Economic Development - «Research Paper of the Univ. of Chicago Dep-t of Geography », 1960, №62.
17. Economic Regionalization and numerical methods. Eds: Berry R., Wrobel A. In: «Geographia Polonica». Warzawa, 1968, vol. 15.
18. Edwards C. Regional Variations in Economic Growth with Emphasis on Rural Areas. - «Agricultural Economic Report», Wash., 1971, № 205.
19. Gould PR Problems of Space Preference Measures and Relationships. - «Geographical Analyses», 1969, vol. 1, № 1.
20. Dauletbakov B Iztaev AI, Aryngazin KS, Omaorov TE, LM Syrlybaeva Simulation of grain quality using factor analysis. Food technology and service. Almaty, 2007. №2. S. 3-7.
21. Iztaev A. Technological quality of wheat in Kazakhstan. - Alma-Ata: Kaynar, 1992, 368 p.
22. Kazakov ED Zernovedenie the basics of crop. "Kolos", Moscow, 1973.
23. http://www.statsoft.com/