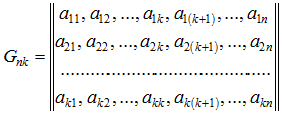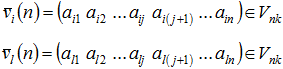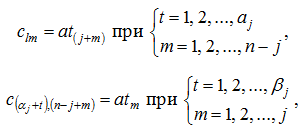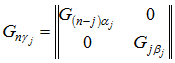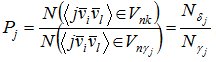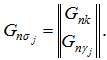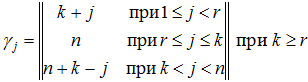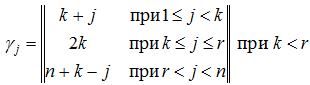ПАРАМЕТРЫ САМОСИНХРОНИЗИРУЮЩИХ СВОЙСТВ ПОЗИЦИОННЫХ ИЗБЫТОЧНЫХ БЛОЧНЫХ КОДОВ

Захарченко Н.В.¹, Корчинский В.В.², Радзимовский Б.К.³, Бектурсунов Д.Н.⁴, Горохов Ю.С.⁵

¹Доктор технических наук, ²Кандидат технических наук, ³Кандидат технических наук, ⁴Аспирант, ⁵Аспирант, Одесская национальная академия связи

ПАРАМЕТРЫ САМОСИНХРОНИЗИРУЮЩИХ СВОЙСТВ ПОЗИЦИОННЫХ ИЗБЫТОЧНЫХ БЛОЧНЫХ КОДОВ

Аннотация

Предложена физика двух подпространств пространства векторов избыточного линейного кода , установлены их порождающие матрицы  и , определены предельные значения мощности пространства пересечений, приводятся рекомендации для отдельных избыточных блоковых кодов.

Ключевые слова: Блоковые коды, корректирующие коды, групповой корректирующий код.

Zakharchenko N.V.¹, Korchinskiy V.V.², Radzimovsky B.K.³, Bektursunov D.N.⁴, Gorokhov Y.S.⁵

¹Ph.D., ²Ph.D., ³Ph.D., ⁴Graduate, ⁵Graduate, Odessa National Academy of Telecommunications;

PARAMETERS SELF-SYNCHRONIZING PROPERTIES

OF POSITIONAL REDUNDANT BLOCK CODES

Abstract

A physics of the two subspaces of vectors excess line code , set their generating matrix  and  defined power limits of space intersection, contains recommendations for individual redundant block codes.

Keywords: Block codes, error-correcting codes, group correction code.

В настоящей работе проводится анализ синхронизирующих свойств групповых кодов (n,k) с позиции обнаружения ошибок, вызванных нарушением цикловой синхронизации излагается методика расчета вероятности необнаруженной ошибки синхронизации с использованием векторно-матричного описания кодов. Приводится методика расчета верхней и нижней границ, соответствующих максимальной и минимальной вероятностям необнаруженной ошибки синхронизации. Эти границы предлагается использовать в качестве критериев для оценки эффективности самосинхронизирующих свойств групповых (n,k) кодов, которые учитываются при выборе корректирующих кодов (КК) для проектируемых СПД.

Кодовые комбинации двоичного (n,k) кода можно рассматривать как векторы п-мерного линейного пространства, соединяющие начало координат с точками, соответствующими вершинам п-мерного гиперкуба с ребрами единичной длины. При этом каждая из координат (разряд кодовой комбинации) может принимать значения 0 или 1.

Совокупность кодовых векторов образует групповой (n,k) код, если данная совокупность образует группу по отношению к заданной алгебраической операции. Для двоичного (n,k) кода этой операцией является сложение по модулю 2.

Групповой корректирующий (n,k) код (ГКК) может быть задан с помощью порождающей матрицы , которая представляет собой набор линейно-независимых (базисных) векторов линейного кода

               (1)

Остальные векторы кодового пространства  образуются путем линейных комбинаций строк порождающей матрицы .

Допустим, последовательно передаются два любых n-элементных кодовых вектора

где i, l = 1, 2, …, 2^k, k – ранг матрицы .

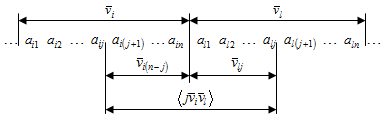
Рассмотрим случай (рис. 1), когда начало отсчета n-элементного кодового вектора на приеме смещается на некоторую величину j относительно переданного, что соответствует нарушению цикловой синхронизации. В результате получим вектор

который назовем вектором пересечения кодовых векторов  и , и обозначим через .

 

Рис. 1 - Границы векторов пересечений

Вектор  можно представить в виде суммы двух векторов: (n-j)-элементного вектора  и j-элементного вектора .

Множество векторов  и  образуют подпространства  и  пространства , которые могут быть заданы порождающими матрицами  и , где α_j и β_j – ранги соответствующих матриц при смещении начала отсчета на величину j. Совокупность векторов  образует пространство векторов пересечений , где  γ_j – размерность пространства . Пространство  является прямой суммой подпространств  и , так как при этом удовлетворяются следующие условия:

                                            (2)

                                             (3)

где + – обозначение прямой суммы, а ∩ – пересечение подпространств.

Выражение (2) означает, что всякий вектор пересечения кодовых векторов  ∈  может быть записан в виде: =+ (∈, ∈), а условие (3) показывает, что подпространства  и  не имеют общих векторов, кроме нулевого.

Так как подпространства  и  задаются порождающими матрицами  и , то пространство векторов пересечений  будет задаваться матрицей , которая определяется прямой суммой подматриц  и , т.е.

 =  + ..

Элементы матрицы  задаются соотношениями:

=0 во всех остальных случаях.

Тогда

                 (4)

Мощность пространства при этом будет равна:

                       (5)

Пространство кодовых векторов  и пространство векторов пересечений  являются подпространствами п-мерного векторного пространства . Возможны случаи, когда векторы, принадлежащие , могут принадлежать и пространству , т.е. имеет место пересечение пространств  и . Это приводит к необнаруженным ошибкам с некоторой вероятностью .

Для определения  обозначим через  пересечение пространств  и . Множество  есть векторное подпространство  каждого из подпространств  и _, и имеет размерность δ_j. Тогда  может быть найдено из

                    (6)

где  – мощность пространства  равная .

Таким образом, для определения вероятности  необходимо найти размерность пространства , т.е. δ_j. Известно, что размерность суммы двух линейных подпространств равна сумме размерностей этих подпространств минус размерность их пересечения. Обозначим размерность суммы подпространств  и  через σ_j, тогда

откуда

        (7)

Значения α_j, β_j и k нам известны. Определение δ_j и σ_j осуществляется следующим образом.

Подпространства  и задаются порождающими матрицами  и , поэтому пространство суммы этих подпространств будет задаваться матрицей , которая имеет вид

                     (8)

Как было отмечено ранее для расчета  необходимо вычислить величины γ_j и δ_j или σ_j. Однако, зная эти величины можно определить  только для случая равновероятной структуры сообщений.

При передаче сообщений, имеющих структуру отличную от равновероятной, что характерно для реальных каналов, полученные результаты будут носить приближенный характер.

В связи с вышесказанным, для расчета  необходимо определить:

• общее количество векторов пересечений 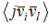, т.е. мощность пространства ;
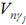• структуру векторов 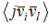∈ 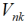 , т.е. найти пространство .

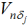Определение мощности пространства  с учетом особенностей структуры групповых (n,k) кодов. Очевидно, что общее количество всех векторов пересечений  при фиксированном j равно

При изменении j от 1 до (n,k), суммарное количество векторов  будет равно

            (8а)

При этом анализ структуры векторов  и определение их количества осуществляется исходя из принципа их формирования (по принципу каждый с каждым векторов  и ). Последнее приводит к громоздким и неудобным вычислениям (методом перебора).

С учетом вышесказанного получаем

                 (9)

Таким образом, величина ранга матрицы  при изменении j от 1 до (n-1) полностью зависит от структуры группового (n,k) кода, в частности от структуры матрицы дополнения  и вычисляется по (8) и (9).

Для групповых кодов характерно такое построение матрицы-дополнения , что с целью достижения наивысшей корректирующей способности по аддитивным ошибкам, она после приведения к каноническому виду, является порождающей для пространства, мощность которого равна 2^r при r<k и 2^k при r>k.

Раскрывая выражения (8), (8а) и (9) можно показать, что

               (9а)

В связи с этим, в случае , величина  будет равна:

а) при 1 ≤ j ≤ r,

                               (10)

б) при r ≤ j ≤ k,

                                         (11)

т.к. в (9а) , следовательно,   и ;

в) при k < j < n,

                             (12)

т.к. , то  будет равен числу ее столбцов, а именно (n-j), поэтому из (9) следует, что .

В случае r>k:

а) при 1 ≤ j < k,

                                 (13)

т.к. в (9а) , следовательно,   и ;

б) при k ≤ j ≤ r,

                                      (14)

т.к. в (9а) , следовательно,   и ;

в) при r < j < n,

                            (15)

т.к. , то  будет равен числу ее столбцов, а именно (n-j), поэтому из этого следует, что .

Систематизируя выражения, получим:

                     (16)

                     (17)

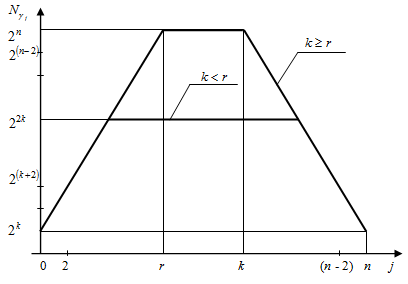
Вычисление мощности пространств векторов  осуществляется по (5). На рис. 2 приведены графики зависимости мощности пространства  от j, n и k, а на рис. 3 зависимости предельных значений Р_j  от структуры используемых кодов и величины смещения j.

Рис. 2. Зависимость мощности пространства  от j, n и k

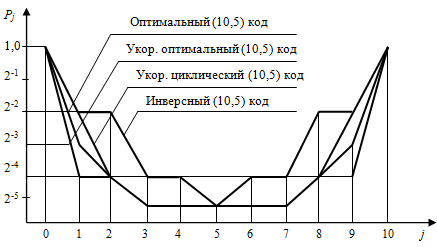
Рис. 3. Зависимость  от величины смещения j

 

Литература

1. Захарченко В.Н., Улеев А.П., Липчанский А.И. Эффективность исправления ошибок смещения ЗМВ в системах с РОС на базе МВС. Вестник Харьковского политехнического университета. – Харьков: ХГПУ, 1999. – Выпуск 35. – С. 85-91.
2. Морелос-Сарагоса Р. Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение. – М.: Техносфера, 2005. – 320 с.
3. Помехоустойчивость и эффективность систем передачи информации. / А.Г. Зюко, А.И. Фалько, И.П. Панфилов, В.Л. Банкет, П.В. Иващенко; Под ред. А.Г. Зюко. – М.: Радио и связь, 1985. – 272 с.
4. Берлекамп Э. Алгебраическая теория кодирования: Пер. с англ. / Под ред. С.Д. Бирмана. – М.: Мир, 1971. – 477с.

References

1. Zakharchenko N. V., Uleyev A.P., Lipchansky A.I. The effectiveness of error correction offset FVW systems with ROS-based MBC. Bulletin of the Kharkov Polytechnic University. - Kharkov: KhSPU, 1999. - Issue 35 - pp 85-91.
2. Morelos-Zaragoza R. Arts noiseless coding. The methods, algorithms, applications. - M .: Technosphere, 2005. - 320 p.
3. Immunity and effectiveness of information transfer. A.G. Zyuko, A.I. Falco, I.P. Panfilov, V.L. Banquet, P.V. Ivashchenko; Ed. A.G. Zyuko. - M .: Radio and Communications, 1985. - 272 p.
4. E. Berlekamp algebraic coding theory: Trans. from English. / Ed. S.D. Birman. - M .: Mir, 1971. - 477s.