ИМИТАЦИОННАЯ МОДЕЛЬ ПЕРЕКРЕСТКА С СИСТЕМОЙ ИНТЕЛЛЕКТУАЛЬНОГО УПРАВЛЕНИЯ

Евдокимов А.О.¹, Горохов А.В.², Лугов Д.Я.³

¹Кандидат технических наук, доцент,

²доктор технических наук, профессор,

³магистрант,

Поволжский государственный технологический университет

ИМИТАЦИОННАЯ МОДЕЛЬ ПЕРЕКРЕСТКА С СИСТЕМОЙ ИНТЕЛЛЕКТУАЛЬНОГО УПРАВЛЕНИЯ

Аннотация

Описана имитационная модель перекрестка с системой интеллектуального управления для реализации в системе имитационного моделирования ANYLOGIC 7.1. Приведеныалгоритмы работы адаптивной и неадаптивной систем управления светофорами на перекрестке. Ключевые слова: перекресток, интеллектуальный перекресток, имитационное моделирование, управление дорожным движением.

EvdokimovA.O.¹, GorokhovA.V.², Lugov D.Ya.³

¹PhD in Engineering, associate professor,

²PhD in Engineering, professor,

³undergraduate,

Volga State University of Technology

SIMULATION MODEL OFTHE JUNCTIONS INTELLIGENT CONTROL SYSTEM

Abstract

A simulationmodel ofthe junction withintelligent controlsystemfor realizationin systemsimulation modelingANYLOGIC 7.1.The algorithms ofthe adaptiveandnon-adaptivecontrol systems oftraffic lightsat the intersection. Keywords: crossroads, intelligent intersection, simulation, traffic management. Введение Постоянно растущие проблемы автодорожного движения в крупных городах стимулируют развитие методов анализа существующей и перспективной ситуаций с целью повышения эффективности использования дорог. Интеграция различных методов и средств позволяет с разных сторон посмотреть на возникающие проблемы. Отчасти, решение такой проблемы видится во внедрении автоматизированных систем управления дорожным движением (АСУДД), применение которых, по оценкам экспертов, позволяет в настоящее время снизить загруженность отдельных участков городской дорожной сети на 30-40% [2]. Их особенность заключается в том, что они управляют работой светофоров не по заранее заложенным алгоритмам и схемам, а подстраиваясь под конкретную ситуацию на дороге, отслеживаемую набором датчиков на каждом перекрестке. Такие системы получили общее название «интеллектуальный перекресток», хотя в настоящее время отечественные и зарубежные компании предлагают большое количество подобных систем, функционирующих на основе различных алгоритмов, в том числе с функциями фиксации нарушений правил дорожного движения (ПДД). Необходимо отметить, что при имеющейся тенденции к увеличению количества транспортных средств (ТС), в среднесрочной перспективе будет фиксироваться снижение эффективности работы «интеллектуальных перекрестков». Таким образом, уже сейчас возникает актуальная задача введения координированного движения транспортных потоков, а также их прогнозирования и гибкого регулирования. Признанным методом анализа транспортных сетей является имитационное моделирование. Преимущество имитационных моделей по сравнению с аналитическими состоит в принципиальной возможности отобразить объект на любом уровне детализации. Объектом управления в системе управления дорожным движением является транспортный поток, состоящий из технических средств (автомобилей, мотоциклов, автобусов и так далее). В то же время водители автомобилей ведут себя на дороге и реагируют на различные события по-разному, не всегда предсказуемо, что значительно усложняет анализ такой системы. Таким образом, дорожное движение представляет собой техносоциальную систему, что и определяет его специфику как объекта управления [8]. Даже рассматривая только технические аспекты управления дорожным движением, необходимо иметь в виду, что этот объект весьма своеобразен и сложен с точки зрения управления его свойствами. Городские транспортные потоки обладают, как правило, следующими особенностями. 1)Стохастичность транспортных потоков: их характеристики допускают прогноз только с определенной вероятностью. Транспортный поток движется по транспортной сети, которая также обладает определенными характеристиками, допускающими более или менее строгое описание, и которые являются нестационарными. 2)Нестационарность транспортных потоков, с колебанием характеристик в суточном, недельном и сезонном циклах. 3)Неполная управляемость, заключающаяся в том, что даже при наличии полной информации о потоках и возможности информирования водителей о необходимых действиях, эти требования носят рекомендательный характер. Следовательно, достижение глобального экстремума любого критерия управления становится весьма проблематичным. 4) Множественность взаимосвязанных характеристик, таких как: задержка в пути, средняя скорость движения, прогнозируемое число дорожно-транспортных происшествий (ДТП), объем вредных выбросов в атмосферу и т.д. 5)Сложность оценки основных характеристик, определяющих качество управления. Так, оценка величины интенсивности движения требует либо наличия датчиков транспортных потоков на всех направлениях их движения, либо использования данных аэрофотосъемки, либо проведения трудоемкого ручного обследования. 6)Невозможность проведения масштабных натурных экспериментов в сфере управления дорожным движением. Эта невозможность предопределена, во-первых, необходимостью обеспечения безопасности движения, во-вторых, материальными и трудовыми затратами на проведение эксперимента (изменение разметки и дислокации дорожных знаков) и, в-третьих, тем, что серьезные изменения в комплексной схеме организации движения затрагивают интересы большого количества людей - участников движения. Перечисленные особенности заметно усложняют построение аналитической модели, позволяющей исследовать варианты управления в АСУДД и ее характеристики в различных условиях. В то же время современные информационные технологии и методы имитационного моделирования имеют большие возможности для решения такого рода задач, что позволяет при наличии адекватной модели быстро и с достаточной точностью прогнозировать характеристики потоков транспортных средств и оптимизировать существенные параметры их движения, руководствуясь общей дорожной ситуацией. Целью работы является создание модели перекресткаcсистемой интеллектуального управления, расположенного на пересечении улицы Карла Маркса и проспекта Ленина в г. Йошкар-Ола, создание библиотеки элементов в среде имитационного моделирования и ANYLOGIC 7.1 и анализ алгоритмов работы адаптивной и неадаптивной систем управления светофорами на указанном перекрестке.

1. Имитационное моделирование транспортных потоков

В настоящее время для моделирования транспортных потоков существует множество специализированных систем имитационного моделирования, таких как, TRANSIMS, PARAMICS, EMME/2, SATURN и др. Большой популярностью пользуются программные продукты немецких производителей, объединяемые названием PTV Vision [1]. Существующие подходы к моделированию могут быть классифицированы в зависимости от уровня детальности моделируемого процесса:

• Модели макроуровня описывают транспортный поток как целое, совокупность всех транспортных средств. Значимые параметры – плотность трафика и т.д. В макромоделях дорожного движения объектами моделирования являются крупные транспортные сети, потоки автомобилей, системы управления потоками. В моделях используются результаты теории систем массового обслуживания, аналитические и имитационные методы.
• Модели микроуровня характеризуются описанием отдельных транспортных средств и взаимодействий между ними. Модели этого класса показывают поведение отдельных участников дорожного движения, подчиняющиеся правилам поведения и взаимодействия транспортных средств. Правила поведения содержат дополнительные стратегии для управления скоростью и ускорением. В настоящее время микроскопические модели используются для моделирования трафика на отдельных перекрестках и их совокупностях.

В микромоделях используются агентный подход [6] клеточные автоматы [7], управляемые (например, светофорами) системы массового обслуживания. Сложности представления микромоделей перекрестков методами аналитического моделирования демонстрирует объемная монография [8]. Как показано в применение специализированных систем целесообразно для анализа и проектирования транспортных сетей крупных городов (Москва, Санкт-Петербург, Красноярск и др.). Для научно-практических работ часто требуются менее мощные, но легко адаптируемые, ориентированные на выполнение конкретных задач методы и средства. К такому классу относится описанная в статье работа. В качестве среды моделирования был выбран пакет ANYLOGIC 7.1 [10]. ANYLOGIC- это универсальный инструмент для моделирования дискретных, непрерывных и гибридных систем. Области его применения разнообразны: от простых обучающих моделей до логически сложных. AnyLogic использует такое мощное средство проектирования сложных систем как UnifiedModelingLanguage (UML, универсальный язык моделирования). Предполагалось, что универсальность пакета, его возможности работать как с непрерывными, так и дискретными моделями, его доступность и простота использования позволят построить модель одного из участков транспортной сети («интеллектуального перекрестка») и создать библиотеку элементов транспортной сети, которая будет удобна для решения широкого круга разнообразных проблем в области транспорта. Кроме того, используемые в пакете ANYLOGICсредства объектно-ориентированного программирования позволяют наглядно отображать, легко адаптировать и настраивать элементы библиотеки.

2. Описание концептуальной модели перекрестка

Построение концептуальной модели предшествует этапу программирования имитационной модели. Реальные перекрестки имеют множество разных конфигураций, полос и направлений движения, способов размещения светофоров. В представленной работе рассматривается перекресток улицы Карла Маркса и проспекта Ленина в г. Йошкар-Оле. В июне 2015 года в Йошкар-Оле будет введен в эксплуатацию новый автомобильный мост через реку Малая Кокшага (Автор проекта моста – филиал Нижегородского проектного института ОАО «Гипродорнии»).

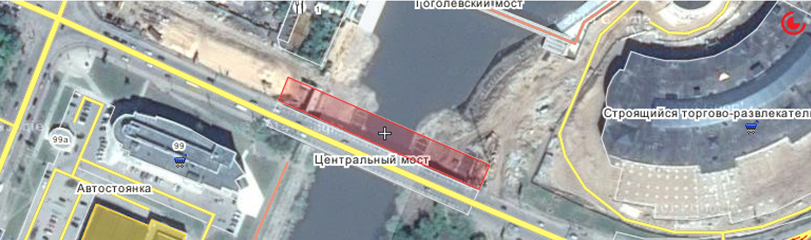
Рис. 1 – Центральный и строящийся мост через р. Малая Кокшага и их развязка в Центральной и Заречной части г. Йошкар-Ола. Спутниковый снимок

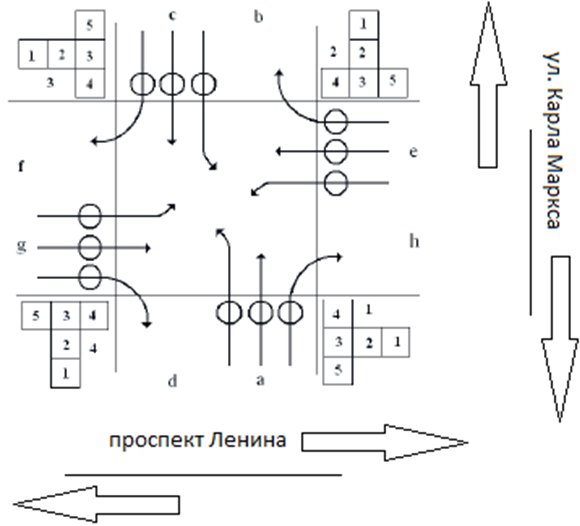
  Строящийся мост располагается параллельно существующему Центральному мосту. Длина моста составит 122 метра, участка строительства – 481 метр (рис. 1). Центральный мост будет реконструирован, и в итоге будут два односторонних моста с тремя полосами движения на каждом и тротуарами. Введение в строй нового моста позволит разгрузить Центральный мост и устранить регулярно возникающие заторы. «Узким местом» проекта является проектируемая развязка в центральной части города (перекресток улицы Карла Маркса и проспекта Ленина). В настоящее время данный перекресток оборудован системой «интеллектуальный перекресток», позволяющей фиксировать нарушения ПДД и оценивать потоки движения ТС, однако, система функционирует в тестовом режиме, что объясняется соображениями безопасности движения. В данной работе предлагается одна из возможных модель реализации развязки после реализации проектов строительства и реконструкции (рис.2). Предложенная модельпозволяет с помощью упрощений отобразить значительное количество конфигураций перекрестков (за исключением самых сложных) [1]. Данная модель не учитывает поведение водителей, ДТП, а также перестроение автомобилей в другой ряд. Для построения более детальных моделей, могут использоваться другие методы, например, метод клеточных автоматов.

Рис. 2 –Модель перекрестка улиц Карла Маркса и проспекта Ленина в г. Йошкар-Ола

  Латинские буквы используются для обозначения потоков автомобилей и направлений движения (курсивом будем обозначать модели реальных объектов). В модели существует четыре потока: a, g, с, e. Для обозначения направлений движения используются пары букв (например, ab, af). В каждом потоке три полосы, движения автомобилей. Каждая полоса предназначена для движения в одном направлении. Кругами обозначены задержки автомобилей перед перекрестком в каждом из направлений. Движением на перекрестке управляют четыре светофора (модели совокупности реальных светофоров). Каждый светофор имеет номер, пять секций и управляет одним потоком. Например, светофор 3 управляет потоком «e», светофор 2 управляет потоком «а». Каждая секция имеет два состояния (светится / не светится). Секция 1 светится красным цветом, секция 2 - желтым, секции 4, 3, 5 - зеленым. Светофор имеет набор состояний. Каждое состояние светофора задается набором состояний секций, разрешающих или запрещающих движение в различных направлениях. Например, зеленые секции 3, 4, 5 светофора 2 разрешают потоку «а» движение во всех направлениях (af, ab, ah). Считается, что светофор имеет 8 состояний. В таблице 1 представлена карта состояний светофора. Единица означает свечение соответствующей секции. При построении имитационной модели реального перекрестка набор реальных светофоров на перекрестке приводится к моделям светофоров концептуальной модели.  

Таблица 1 – Карта состояния светофора

Состояние светофора	Секция 1	Секция 2	Секция 3	Секция 4	Секция 5
1	1	0	0	0	0
2	0	1	0	0	0
3	0	0	1	0	0
4	0	0	0	1	0
5	0	0	0	0	1
6	0	0	1	1	0
7	0	0	1	0	1
8	0	0	1	1	1

  Алгоритм перехода светофоров в разные состояния задается системой управления светофорами (СУС). В модели различаются неадаптивные (детерминированные) и адаптивные СУС. Неадаптивные СУС (НСУС) переключают состояния светофоров через заранее заданное время. Адаптивные СУС (АСУС) переключают состояния светофоров с учетом текущей ситуации на перекрестке (например, с учетом длин очередей в различных направлениях). На перекрестке в каждом направлении существует очередь, управляемая светофорами. В моделях на уровне классических систем массового обслуживания тонкости управления светофорами обычно не учитываются. В предлагаемой модели очереди зависят не только от задержек и интенсивностей потока транспортных средств, но и от используемой системы управления. Также будем считать, что интенсивность поступления транспортных средств на перекресток в каждом из направлений зависит от предыдущей задержки (предыдущий светофор, переход).

3. Модель направления движения

В каждом направлении движения происходят задержки, величины которых зависят от состояний светофоров и очередей автомобилей перед перекрестком. В модели на рис. 2 представлены 12 направлений движения. Например, движение в направлении «ab» разрешено в том случае, когда светофор с номером 2 находится в состоянии 8. Движение в направлении «ah» разрешено при нахождении светофора с номером 2 в состоянии 8, либо в состоянии 5. В таблице 2 приведены состояния светофоров, разрешающих движение для каждого из направлений. Реализована следующая схема имитации прохождения автомобилей в каждом из 12 направлений.

1. Генерация потока транспортных средств.
2. Постановка автомобиля в очередь перед перекрестком.
3. Ожидание освобождения первого места перед перекрестком (Т1).
4. Постановка автомобиля на первое место перед перекрестком.
5. Ожидание сигнала светофора, разрешающего движение (T2).
6. Проезд первого места перед светофором (Т3).
7. Освобождение первого места перед светофором.
8. Выход из очереди перед перекрестком.
9. Пересечение перекрестка (Т4).

 

Таблица 2 – Направления движения и состояния светофора

№	Направление	Светофор	Номер основного состояния светофора, разрешающего проезд	Номер вспомогательного состояния светофора, разрешающего проезд
1	ab	2	8	0
2	ah	2	8	5
3	af	2	8	0
4	cf	4	8	5
5	cd	4	8	0
6	ch	4	8	0
7	ed	3	8	0
8	ef	3	8	0
9	eb	3	8	5
10	gd	1	8	5
11	gh	1	8	0
12	gb	1	8	0

  На первом этапе для направления задается закон распределения времени между поступлением транспортных средств на перекресток. В каждом конкретном случае интенсивность поступления автомобилей зависит от типа предыдущей задержки (светофор, переход, перекресток), от времени суток и времени года. Поступающие к перекрестку автомобили становятся в очередь. Считается, что в каждом направлении образуется очередь автомобилей, независимая от других направлений (перестроения между полосами движения не учитываются). Если первое место перед перекрестком занято, автомобиль ожидает его освобождения в течение времени Т1 (этап 3). При освобождении первого места ближайший к нему автомобиль становится первым перед перекрестком (этап 4). Если нет разрешающего сигнала светофора, автомобиль ожидает его в течение времени Т2 (этап 5). При получении разрешающего сигнала светофора автомобиль проезжает первое место за время Т3 (этап 6) и освобождает первое место для следующего за ним автомобиля (этап 7). Считается, что после этого автомобиль выходит из очереди перед перекрестком (этап 8). Таким образом, время нахождения автомобиля в очереди перед перекрестком Tq равно сумме Т1, Т2 и Т3. Затем автомобиль пересекает перекресток за время Т4 и транспортное средство, выполнившее движение, удаляется из модели. Общее время задержки при прохождении автомобилем перекрестка равно сумме Tq и Т4. Модель статической (неадаптивной) системы управления светофорами (НСУС). В имитационной модели (ИМ) реализуется описанная концептуальная модель перекрестка.  

Таблица 3 – Состояния неадаптивной системы управления

Номер состояния	S1	S2	S3	S4	Cледующеесостояние	Поток 1	Поток 2
1	5	8	1	1	2	ab, ah, af	gd
2	1	1	5	8	3	cf, cd, ch	ab
3	1	5	8	1	4	ed, ef, eb	ah
4	8	1	1	5	1	gd, gh, gb	cf

  Модель НСУСимеет ряд состояний, управляющих состояниями светофоров. Набор состояний системы управления и последовательность переходов между состояниями зависит от заданных характеристик конкретного перекрестка. Алгоритм функционирования НСУС, используемый в ИМ приведен в табл. 3. Модель динамической (адаптивной) системы управления светофорами (АСУС). Адаптивная АСУС учитывает текущее состояние перекрестка.Существует множествореализаций алгоритмов для АСУС. В рассматриваемой имитационной модели реализована простейшая модификация НСУС, которую при современных средствах видеонаблюдения технически нетрудно реализовать. АСУС переходит в следующее состояние либо при отсутствии автомобилей во всех открытых направлениях, либо по истечении заданного времени нахождения в состоянии для НСУС. Описанная модель позволит исследовать различные характеристики транспортных систем для решения проблем анализа и оптимизации транспортных потоков. В рамках пакета ANYLOGIC возможно выполнение оптимизации модели, т.е. получение оптимальных значений каких-либо параметров модели при заданном критерии оптимизации. В модели транспортной системы при оптимизации можно изменять параметры и/или функциональность объектов транспортной системы. Критерии оптимизации могут не совпадать для различных элементов системы, цели оптимизации также могут быть противоположны. Поэтому, следует строить сложные критерии оптимизации с использованием весовых функций. Время создания модели транспортной сети зависит от её объема. Построение транспортных сетей и проведение несложных экспериментов с ними может быть выполнено даже не имеющим специальной подготовки пользователем. Заключение Предлагаемая модель перекрестка может быть использована в различных работах по оценке простоя автомобилей в очередях. Преимуществами данного подхода к моделированию и исследованию транспортных сетей в пакете ANYLOGIC является простота и наглядность построения сети, возможность расширения и усовершенствования модели пользователем. Такое исследование можно проводить в нескольких направлениях:

1. Анализ конкретных ситуаций, когда моделируется реальная ситуация (например, авария, уборочные работы), в которой анализируются такие характеристики системы, как средняя скорость движения ТС, время ожидания в очередях (задержки в пути) и т. п.
2. Поиск оптимального решения некоторых задач управления движением, для чего необходимо выбрать изменяемые параметры (например, времена переключения светофоров, количество полос движения и др.) и определить целевую функцию (оптимизируемое значение). Такой функцией может быть, например, средняя скорость на анализируемом участке транспортной сети, время ожидания на перекрестках и т.д.
3. Прогнозирование влияния изменения топологии транспортной сети (строительство объездных дорог, введение датчиков наличия ТС на перекрестке, изменение типов перекрестков и т.д.) на важные характеристики транспортного потока.
4. Борьба с пробками на дорогах. Данная задача решается уменьшением интенсивности движения в заданном направлении, например, перенаправлением транспортного потока на прилегающие дороги.

Для апробации модели необходимо провести анализ её адекватности реальному процессу дорожного движения. Для проведения такого исследования требуется измерение входные данные для модели сети (средний интервал появления ТС, статические параметры транспортной сети, параметры движения ТС) и выходные характеристики (средние длины очередей на перекрестках, средние времена ожидания ТС). Затем в процессе моделирования и выполнения процедур оптимизации может быть оценен эффект от использования различныхадаптивных алгоритмов управления светофорами.

Литература

1. Пуртов, А. М. Разработка и анализ имитационной модели перекрестка для системы GISAUTO / А. М. Пуртов // Омский научный вестник. - 2013. - № 1(117). - С. 225- 229.
2. Храпова, С.М. Определение уровня загрузки автомобильным транспортом городских магистралей: диссертация на соискание ученой степени кандидата технических наук: 05.22.10 / Храпова Светлана Михайловна; [Место защиты: Иркут. гос. техн. ун-т].- Омск, 2010.- 182 с.: РГБ ОД, 61 10-5/1492.
3. Ахмадинуров, М.М. Оптимизация светофорного регулирования с помощью программы моделирования транспортных потоков // Вестник ЮУрГУ, № 22, 2010. 26-30.
4. Пуртов, А.М. Интеграция технологии ГИС и метода редукции графов для анализа транспортных сетей/ А. М. Пуртов // Омский научный вестник. - 2011. - № 1(97). - С. 164- 168.
5. Лукин, В.А. Учет влияния параметров улично-дорожной сети на условия безопасности движения в городах/ В.А.Лукин, А.В.Лукин// Вестник ХНАДУ. - 2009. №47. С.45-57.
6. Юршевич, Е. А. Опыт использования пакета ANYLOGIC для моделирования городского трафика / Е. А. Юршевич, Е. И. Петрова // Имитационное моделирование. Теория и практика (ИММОД-2005): сб. докл. 2-й Всерос. конф. Т. 1. - СПб.: ЦТ СС, 2005. - С. 298 - 305.
7. Долгушин, Д. Ю. Двухуровневое моделирование автотранспортных потоков на основе клеточных автоматов и систем с очередями / Д. Ю. Долгушин, В. Н. Задорожный, С. В. Кокорин // Имитационное моделирование. Теория и практика (ИММОД-2011): материалы 5-й Всерос. конф. Т. 1. - СПб.: ЦТ СС, 2011. - С. 139-144.
8. Живоглядов, В. Г. Теория движения транспортных и пешеходных потоков / В. Г. Живоглядов. - Ростов н/Д.: Изд-во журн. «Изв. вузов. Сев.-Кавк. регион», 2005. - 1082 с.
9. Яцкив, И. В. Использование возможностей имитационного моделирования для анализа транспортных узлов / М. В. Яцкив, Е. А. Юршевич, Н. В. Колмакова // Имитационное моделирование. Теория и практика (ИММОД-2005): сб. докл. 2-й Всерос. конф. Т. 2. - СПб.: ЦТ СС, 2005. - С. 237 - 245.
10. http://www.anylogic.ru

Reference

1. Purtov A. M. Razrabotka i analiz imitatsionnoi modeli perekrestka dlya sistemy GISAUTO [Development and analysis of the simulation model of intersection for the GISAUTO’s system]. Omskii nauchnyi vestnik, 2013,  No. 1(117), pp. 225- 229.
2. Khrapova, S.M. Opredelenie urovnya zagruzki avtomobil'nym transportom gorodskikh magistralei [Determining the level of loading road city roads]. Candidate’s Dissertation in Technical Sciences (Irkutsk GU, Omsk, 2010)
3. Akhmadinurov, M.M. Optimizatsiya svetofornogo regulirovaniya s pomoshch'yu programmy modelirovaniya transportnykh potokov [Optimization of traffic signalization using simulation program transport streams]. Vestnik YuUrGU, 2010, No 22, pp. 26-30.
4. Purtov, A.M. Integratsiya tekhnologii GIS i metoda reduktsii grafov dlya analiza transportnykh setei [Integration of GIS technology and the reduction method of graphs for analysis of transport networks]. Omskii nauchnyi vestnik, 2011, No 1(97), pp. 164- 168.
5. Lukin, V.A. Uchet vliyaniya parametrov ulichno-dorozhnoi seti na usloviya bezopasnosti dvizheniya v gorodakh [Registration the effects of parameters of the road network on the safety conditions in cities]. Vestnik KhNADU, 2009, No 47, pp.45-57.
6. Yurshevich, E. A. Opyt ispol'zovaniya paketa ANYLOGIC dlya modelirovaniya gorodskogo trafika [Experience using ANYLOGIC package for modeling urban traffic]. E. A. Yurshevich, E. I. Petrova Imitatsionnoe modelirovanie. Teoriya i praktika [Simulation modeling. Theory and practice]. (IMMOD-2005), Report coll., 2-nd All-Rus. conf. Vol. 1, SPb,  TsT SS, 2005, pp. 298 - 305.
7. Dolgushin, D. Yu. Dvukhurovnevoe modelirovanie avtotransportnykh potokov na osnove kletochnykh avtomatov i sistem s ocheredyami [Two-level simulation of motor flows based on cellular automata and systems with queues], D. Yu. Dolgushin, V. N. Zadorozhnyi, S. V. Kokorin, Imitatsionnoe modelirovanie. Teoriya i praktika[Simulation modeling. Theory and practice] (IMMOD-2011), materials of 5-th All-Rus. conf. Vol. 1, SPb, TsT SS, 2011, pp. 139-144.
8. Zhivoglyadov, V. G. Teoriya dvizheniya transportnykh i peshekhodnykh potokov [Theory of traffic and pedestrian flows]. V. G. Zhivoglyadov, Rostov-on-Don, Izv. vuzov. Sev.-Kavk. region, 2005. - 1082 s.
9. Yatskiv, I. V. Ispol'zovanie vozmozhnostei imitatsionnogo modelirovaniya dlya analiza transportnykh uzlov [Using the power of simulation modeling for assaying of transport hubs] M. V. Yatskiv, E. A. Yurshevich, N. V. Kolmakova Imitatsionnoe modelirovanie. Teoriya i praktika [Simulation modeling. Theory and practice] (IMMOD-2005), Report coll., 2-nd All-Rus. conf. Vol. 2, SPb, TsT SS, 2005, pp. 237 - 245.
10. http://www.anylogic.ru