Об одном способе дискретизации задачи Фишера-Колмогорова-Петровского-Пискунова
Об одном способе дискретизации задачи Фишера-Колмогорова-Петровского-Пискунова
Аннотация
В настоящей статье для квазилинейного уравнения Фишера-Колмогорова-Петровского-Пискунова исследуется двухслойная шеститочечная разностная схема с весами, которая обладает первым порядком аппроксимации по временной переменной и вторым по пространственной. С использованием принципа максимума в работе получена априорная оценка разностного решения. Доказывается монотонность разностной схемы, сконструированной относительно сеточной функции, представляющей собой разность между решением разностной задачи с возмущенными входными данными и решением исходной разностной задачи. Получена оценка в сеточном аналоге нормы С, выражающая устойчивость схемы по отношению к малому возмущению всех входных данных. Приведены результаты численного эксперимента.
1. Введение
Базовой математической моделью среды, для которой характерна пространственно-временная самоорганизация, выступает нелинейное уравнение реакции-диффузии (УРД):
В 1937г. Р. Фишер
и советские математики А.Н. Колмогоров, И.Г. Петровский и Н.С. Пискунов разработали модель, основанную на уравнении из класса уравнений реакции-диффузии:Уравнение Фишера-Колмогорова-Петровского-Пискунова (Ф-КПП) (1) играет большую роль в исследовании биологических, химических и социальных процессов. Справедливости ради, стоит отметить, что первоначально уравнение было предложено Г. Хотеллингом в 1921 г.
в качестве модели, описывающей популяционный рост и распространение.В статье приводятся необходимые и достаточные условия интегрируемости и общей мероморфности решений уравнений типа Фишера, получены точные решения типа бегущей волны. Для практических нужд важно не только исследование качественных свойств решения рассматриваемого уравнения
, но и применение численных методов .Одним из методов получения априорных оценок для решений разностных схем, а также исследования устойчивости является принцип максимума. Принцип максимума дает только достаточные условия устойчивости, то есть из их невыполнения не следует, что схема неустойчива. Из априорных оценок в сеточных нормах следует устойчивость решения разностной схемы по отношению к малым возмущениям входных данных задачи. В нелинейном случае из полученных априорных оценок не следует ни единственность сеточного решения, ни устойчивость. Для того чтобы пользоваться доказательным аппаратом принципа максимума, требуется построение разностной схемы, которая была бы монотонна относительно разности между решением разностной задачи с возмущенными входными данными и решением исходной задачи.
2. Априорная оценка решения разностной схемы
Рассмотрим в прямоугольнике
начально-краевую задачу для одномерного уравнения Фишера-Колмогорова-Петровского-Пискунова:
Далее будем предполагать неотрицательность входных данных (3)-(4).
Введем равномерную сетку
Для аппроксимации рассматриваемой нелинейной задачи применим следующую линейную разностную схему с весами:
где параметры
Начальные и краевые условия аппроксимируем точно
Ранее в работе было доказано, что схема обладает первым порядком аппроксимации по
Используя технику принципа максимума , найдем априорную оценку.
Пусть в ограниченной области задана сетка
Выделим в качестве центрального узла тот узел, у которого коэффициент
Шаблон
Далее будем полагать, что коэффициенты уравнения (9) удовлетворяют условиям неотрицательности:
для любого внутреннего узла
Приведем ряд теорем, доказанных в
.Пусть
Теорема 1. (принцип максимума)
Пусть
Теорема 2.
Пусть функция
Тогда
Если же
Следствие 1.
Пусть выполнены условия (10) и
Теорема 3. (теорема сравнения)
Пусть
где
Тогда, если
Следствие 2.
Для решения однородного уравнения
справедлива оценка
где
Теорема 4.
Пусть коэффициенты уравнения (9) удовлетворяют условиям:
тогда для решения задачи (9) c нулевым граничным условием
где
Таким образом, условия положительности коэффициентов
гарантируют однозначную разрешимость, монотонность и устойчивость в равномерной норме по отношению к малому возмущению входных данных.
Разностное уравнение (5) можно переписать в виде
Пусть
Тогда
Определим условия, при которых схема принадлежит рассматриваемому классу.
Рассмотрим коэффициент канонической формы
Покажем, что
Если
Будем рассматривать случай, когда
неравенство (12) истинно.
Нетрудно видеть, что для
Пусть
Если
то в этом случае
В рассматриваемой задаче при выполнении условий (14)-(15) имеет место неравенство
Тогда коэффициент
Положительность
Пусть
Теорема 5. Пусть выполнены условия
и разностное решение
Тогда справедлива двусторонняя оценка:
Доказательство.
Будем следовать методике доказательства, изложенной в работе [10, C. 391-398].
На нулевом слое справедлива следующая оценка
По индукции предположим, что оценка (18) верна также и для всех
Максимум и минимум сеточной функции может достигаться либо на границе, либо во внутренней точке сетки.
Запишем оценку, доказанную в работе [11, P. 186–199]:
где
Тогда
C учетом (20):
Что и требовалось доказать.
Назовем
Будем рассматривать равномерную сеточную норму
Следствие.
Для решения разностной схемы (5)-(7) справедлива априорная оценка
3. Исследование монотонности и устойчивости
Нижеприведенное определение справедливо разностных схем, аппроксимирующих как линейные, так и нелинейные краевые задачи.
Определение 1. Пусть разностная схема
аппроксимирует дифференциальную задачу
и
Тогда разностная схема (21) называется монотонной, если из условий
следует
Будем рассматривать сеточную функцию
(5)-(7), а
Тогда поэлементно вычитая из (23)-(25) уравнения (5)-(7), получим задачу для сеточной функции
Здесь коэффициенты
Коэффициенты
Выше была доказана положительность этих коэффициентов, содержащих в формуле
Определим условия при которых
Рассмотрим множитель, входящий в первое слагаемое последней формулы:
Вариант
Для случая
Применим двустороннюю оценку (19) к функции
где
Рассмотрим отношение
Если выполнена оценка
и для всех
то из отношения (27) следует
Следовательно, в соответствии с определением 1 разностная схема (5)-(7) является монотонной.
Исследуем устойчивость разностной схемы. Сеточная функция
Объединим оценки:
Неравенство (29) демонстрирует устойчивость разностной схемы (5)–(7) при выполнении условия (28) по отношению к малому возмущению входных данных.
4. Численный эксперимент
Рассмотрим задачу:
Приведем результаты численного эксперимента для начально-краевой задачи (30)-(31), которая была получена из исходной задачи установлением параметров
Численная реализация метода прогонки производилась на языке Python с весовыми коэффициентами
Количество отрезков разбиения по оси
Графики демонстрируют, что численное решение в моменты времени
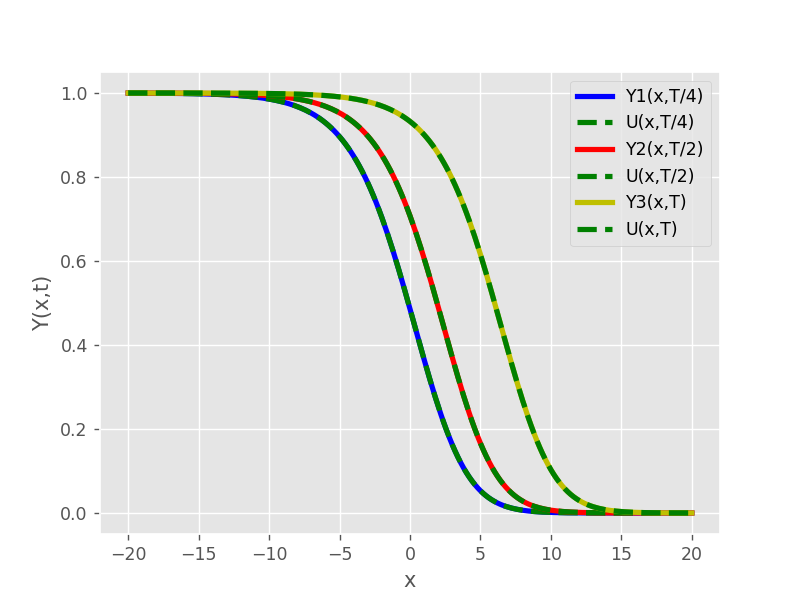
Рисунок 1 - Численное и точное решения в различные моменты времени для M=200, N=400, σ=0,5, β = 0,5.
В таблице 1 приведены абсолютные ошибки численного решения на разных временах, полученные при расчете с параметрами
Таблица 1 - Абсолютные ошибки в разные моменты времени для одного значения шага пространственной сетки и двух значений шага временной сетки
M | Error t1 | Error t2 | Error t3 |
400 | 2.65924e-08 | 2.08158e-08 | 7.09457e-08 |
1000 | 2.78334e-08 | 2.17883e-08 | 7.42831e-08 |
Таблица 2 - Относительные ошибки в разные моменты времени для одного значения шага пространственной сетки и двух значений шага временной сетки
M | Error t1 | Error t2 | Error t3 |
400 | 2.65932e-06 | 2.08191e-06 | 7.09721e-06 |
1000 | 2.78342e-06 | 2.17919e-06 | 7.43107e-06 |
5. Заключение
В данной работе построена и исследована разностная схема для квазилинейного параболического уравнения Ф-КПП. Получены двусторонние оценки разностного решения, доказаны монотонность и достаточное условие устойчивости рассмотренного метода в сеточном аналоге нормы
