АППРОКСИМАЦИЯ НЕКОТОРЫХ КРИВЫХ РАВНОВЕСИЯ БИНАРНЫХ СИСТЕМ АНАЛИТИЧЕСКОЙ ЗАВИСИМОСТЬЮ

Кривые равновесия бинарных систем пар-жидкость представляют собой важный элемент в области физической химии и химической технологии, поскольку они иллюстрируют взаимосвязь между составом паровой и жидкой фазами при достижении термодинамического равновесия. Данные кривые позволяют исследовать и углубленно анализировать поведение различных смесей, что имеет широкое применение при анализе физико-химических процессов. Определение кривых равновесия может осуществляться экспериментально, путем измерения состава паровой и жидкой фаз при заданных термодинамических условиях. В типичной ситуации для оценки термодинамических свойств и поведения бинарных систем пар-жидкость, приходится использовать табличные данные, полученные эксперементальным путём

Среди равновесных кривых многие из них имеют похожую геометрическую структуру. Это позволяет предложить формулу, аппроксимирующую экспериментальные данные, зависящую от определенного числа параметров, подбором которых можно добиться высокой точности аппроксимации.

В данной работе используется двухпараметрическая формула:

В этом случае х — это мольная доля низкокипящего компонента (НК) в жидкой фазе, у*(х) — равновесная концентрация НК между паром и жидкостью, α и β — параметры, выбор которых позволяет аппроксимировать реальные системы. Соотношение (1) дает возможность аналитически находить определенные интегралы типа числа единиц переноса, встречающиеся при описании процессов перегонки, ректификации и возможно некоторых других. Данное соотношение было предложено и использовано для описания отмеченных процессов в насадочных колоннах в работах

Зависимость (1) удовлетворяет необходимым для равновесной функции требованиям: у*(0)=0, у*(1)=1. Отметим, что соотношение (1) не может аппроксимировать системы, имеющие азеотропную точку. Такая аппроксимация нецелесообразна, когда азеотропная точка имеет важное значение для описания конкретного процесса. В этом случае формулу (1) можно использовать в интервале от x = 0 до координаты азеотропной точки.

Заметим, что в частном случае α+β=1 формула (1) сводится к известной зависимости Рауля

Отметим также, что аппроксимационное соотношение (1) можно использовать и при расчете процессов (например абсорбции) когда кривая равновесия расположена ниже диагонали y = x (например кривая 3 рис. 1).

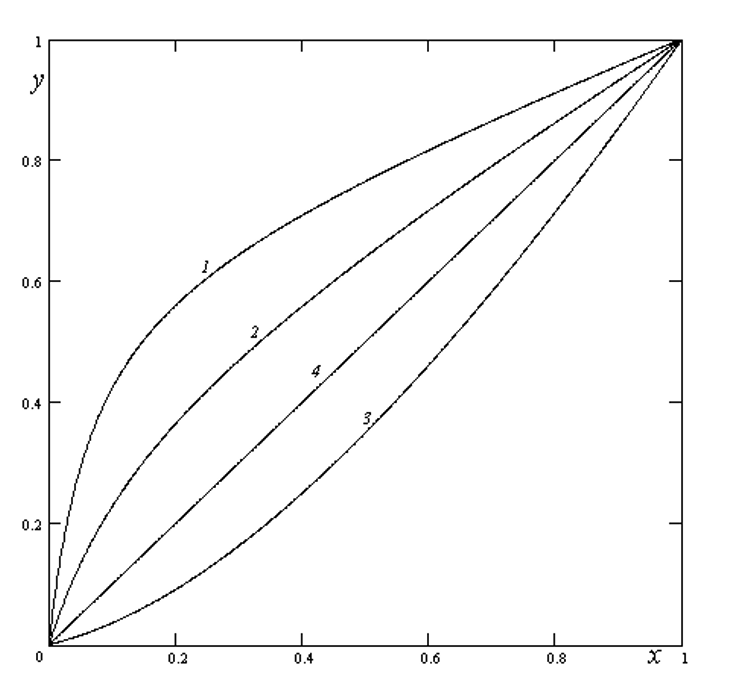
Рисунок 1 - Равновесные кривые y*(x) определяемые формулой (2)

Примечание: 1 – α = 1,5, β = 0,1; 2 – α = 1,9, β = 0,3; 3 – α = 2, β = 4; 4 – диагональ y = x (β = 1)

DOI:10.60797/IRJ.2025.155.83.1

Проверка пригодности формулы (1) на конкретной системе

[5]

показала достаточную для практики точность. В связи с этим целью данной работы является распространение этой формулы на ряд других бинарных систем. Задачей исследования будет подбор коэффициентов α и β для некоторых систем и оценка погрешности соответствия экспериментальных и теоретических данных.

В таблице представлены результаты, полученные путём обработки данных по равновесной кривой методом наименьших квадратов для ряда систем.

Там же приведены соответствующие данные об среднеквадратичном отклонении экспериментальных данных от рассматриваемой зависимости (1). Эта величина определяется так:

где N — это число экспериментальных точек, y*(xj) – значение эксперимен­тальной равновесной функции в точке xj. Поиск оптимальных значений параметров α и β проводится с помощью стандартной программы системы MathCad. При этом задавалось начальные приближенные значения этих параметров. В качестве наглядной иллюстрации точности апроксимации формулой (1) на рис. 2 представлена конкретная система.

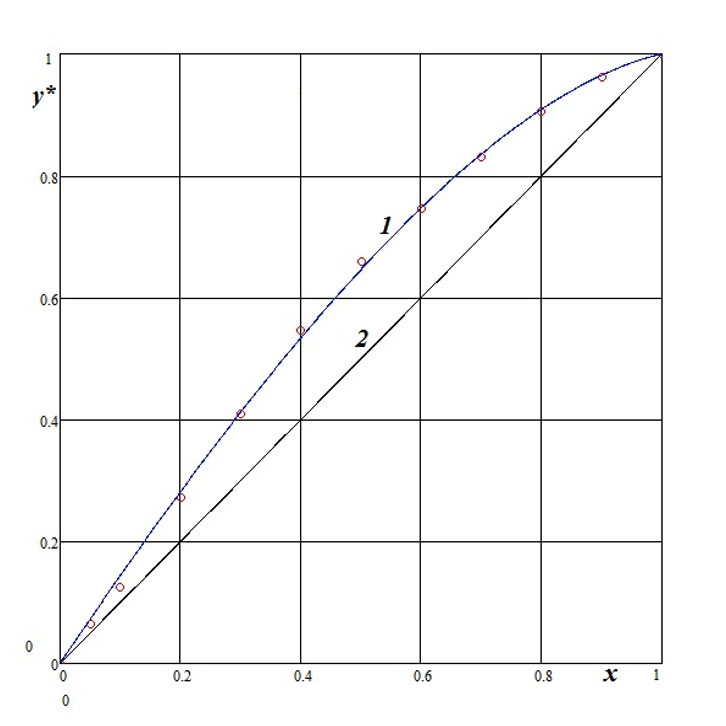
Рисунок 2 - Равновесная кривая y*(x) бинарной системы хлороформ-бензол

Примечание: 1 – равновесная кривая; 2 – диагональ

DOI:10.60797/IRJ.2025.155.83.3

На рис. 2 можно увидеть аппроксимацию бинарной системы хлороформ-бензол: точки °– это экспериментальные данные, линия 1 – равновесная кривая, полученная с помощью формулы (1) и данных таблицы.

При описании некоторых процессов требуется знать равновесную кривую в меньшем интервале независимой переменной, чем рассматриваемом здесь х ∈ (0 , 1). В таком случае можно добиться меньшей погрешности, определяемой формулой (2). То есть формула (1) становится более надежной, чем при параметрах, представленных в таблице.

В качестве примера использования формулы (1) приведем расчетную зависимость для известного

где G — количество жидкости в кубе испарителе, GF — начальное количество перегоняемой смеси, x — состав НК в жидкости, xf — содержание НК в начальной смеси, y* — равновесная концентрация НК в паре. Для уравнения (3) после подстановки в него соотношения (1) и выполнения интегрирования, получаем выражение

Например, для системы бензол-толуол, взяв соответствующие значения параметров α = 0,568 и β = 0411 из таблицы, из формулы (4) следует выражение

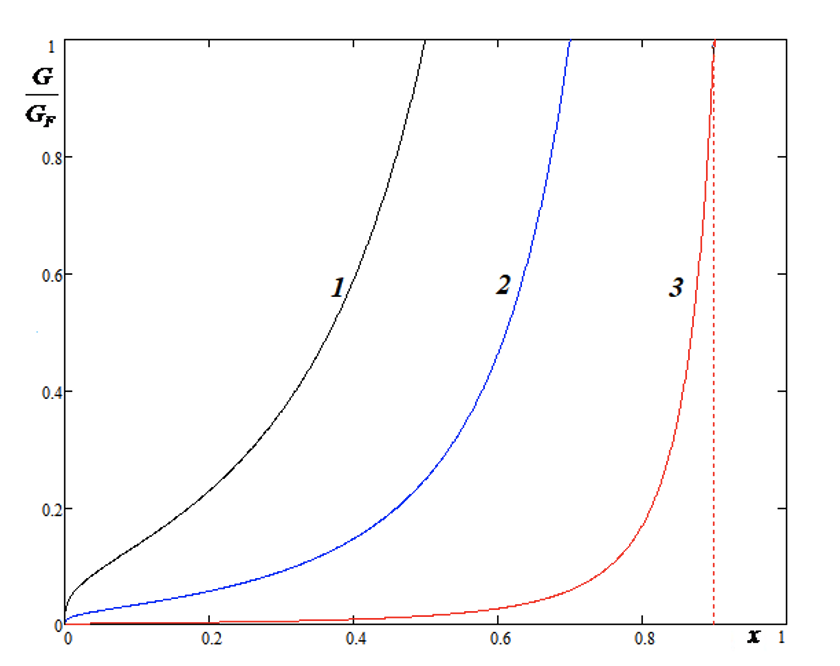
Рисунок 3 - Графики функции G/GF, определенные зависимостью (5)

Примечание: 1 – xf = 0,5; 2 – xf = 0,7; 3 – xf = 0,9

DOI:10.60797/IRJ.2025.155.83.4

Три кривые, в качестве примеров, приведены на рис. 3. Для кривой 3 пунк­тирная вертикальная линия, соответствующая x = xf = 0,9 иллюстрирует, что при этом G/GF = 1, что имеет место и при других xf, в частности показанных на рис 3 кривые 1 и 2, что вытекает из соотношения (4). При малых значениях состава x, формула (5) показывает, что в окрестности нуля функция G/GF степенная.

В соответствии с целью работы, получены данные об аппроксимации некоторых бинарных систем при равновесии, которые представлены в таблице 1, что представляет новизну этой работы. Естественно, что формулу (1) можно использовать и для ряда других, не рассмотренных здесь систем.

Далее, найдена оригинальная (новая) функция простого вида (4) для описания процесса простой перегонки.

Таким образом, статья представляет интерес для исследования процессов ректификации, перегонки бинарных систем и ряда других процессов, кривые равновесия для которых хорошо описываются зависимостью (1), предлагая аппроксимирующую формулу, которая может быть использована для более точного моделирования и оптимизации процессов разделения в различных промышленных и научных приложениях.