МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДИНАМИЧЕСКИХ ПРОЦЕССОВ ПРИ РАБОТЕ КРАНА УПРАВЛЕНИЯ СТОЯНОЧНОЙ ТОРМОЗНОЙ СИСТЕМОЙ АВТОМОБИЛЯ
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДИНАМИЧЕСКИХ ПРОЦЕССОВ ПРИ РАБОТЕ КРАНА УПРАВЛЕНИЯ СТОЯНОЧНОЙ ТОРМОЗНОЙ СИСТЕМОЙ АВТОМОБИЛЯ
Аннотация
Разработана математическая модель динамических процессов функционирования крана управления стояночной тормозной системой – одного из важных и ответственных управляющих аппаратов пневматического тормозного привода современных автомобилей. Данная математическая модель аппарата включает уравнения динамического равновесия его подвижных элементов, а также дифференциальные уравнения газодинамических процессов, протекающих в кране управления стояночной тормозной системой в процессе его функционирования. Уравнения газодинамических процессов в модели составлены на основе гиперболических функций расхода газа в системе «емкость – регулируемый дроссель» с учетом динамики открытия и закрытия клапанов крана управления стояночной тормозной системой в процессе его работы при затормаживании и растормаживании автомобиля. Отличительной особенностью математической модели является то, что она описывает процессы в аппарате пневматического тормозного привода, который функционирует на основе «обратной логики», то есть затормаживание происходит при выпуске рабочего тела из исполнительных аппаратов пневматического тормозного привода, а растормаживание – в процессе их наполнения. Полученные результаты расчетов динамических процессов функционирования крана управления стояночной тормозной системой автомобиля в виде временных, а также в виде фазовых динамических характеристик хорошо согласуются с результатами, полученными в процессе его экспериментальных исследований на компьютерном комплексе ИРНИТУ. Разработанная математическая модель, позволяет расчетными методами получать и исследовать фазовые динамические характеристики крана управления стояночным тормозом. Она позволяет конструкторам-разработчикам аппаратов пневматического тормозного привода оптимизировать конструкцию аппаратов с обратной логикой, с учетом вариации его геометрических, кинематических и силовых параметров, а специалистам в области эксплуатации, разрабатывать методы неразрушающего контроля параметров их технического состояния.
1. Введение
Кран управления стояночной тормозной системой (КУС), предназначен для наполнения и опорожнения рабочим телом (очищенным, сжатым воздухом) исполнительных аппаратов стояночной тормозной системы автомобилей, оснащенных пневматическим тормозным приводом (ПТП) . Он является аналоговым управляющим аппаратом пневматического тормозного привода (ПТП) с механическим приводом, выполняющим функции не только фиксирования неподвижного состояния автомобиля, но и функции запасной тормозной системы, которая вступает в работу при отказе основной тормозной системы автомобиля. Именно поэтому от его быстродействия зависит активная безопасность колесных транспортных средств с пневматическим тормозным приводом , .
Отличительной конструктивной особенностью крана управления стояночной тормозной системой является его функционирование на основе обратной логики. Понятие «обратная логика» заключающегося в том, что для затормаживания автомобиля стояночной тормозной системой, КУС выпускает сжатый воздух из исполнительных аппаратов ПТП, а для растормаживания — наполняет их , . Помимо функциональных требований КУС призваны обеспечивать следящее действие (по перемещению рычага управления), иметь высокое быстродействие, а также быть герметичными , , .
К сожалению, в настоящее время в процессе контроля качества изготовления, а также контроля технического состояния КУС применяют статический метод, при котором измеряют давление на выходе КУС при заданных дискретных положениях его рычага управления , . Метод весьма трудоемкий и крайне малоинформативный , . Попытки разработать динамический метод испытаний КУС сдерживает отсутствие добротной математической модели, с помощью которой можно было бы получить информативные фазовые характеристики КУС , , . Наличие такой модели позволит выявить закономерности между кинематическими, силовыми и геометрическими параметрами, влияющими на работоспособность КУС и его динамические характеристики. В конечном итоге это позволит значительно повысить активную безопасность колесных транспортных средств с пневматическим тормозным приводом.
2. Методы и принципы исследования
С учетом вышеперечисленных требований авторами была составлена расчетная схема (рис. 1) позволяющая выполнить математическое описание динамических процессов в КУС ПТП автомобиля. Начало координат Х0 - Х2 соответствует исходному состоянию органа управления и наличию в КУС давления рабочего тела.
Нами было разработано описание динамики перемещения элементов крана с учетом параметров технического состояния КУС.
С использованием расчетной схемы (см. рис. 1) были составлены уравнения динамического равновесия всех подвижных элементов крана. При этом управляющее воздействие на КУС задавали в виде изменения угла поворота Uвх =a (t) рычага 2 крана с заданной интенсивностью .
Используя расчетную схему КУС, были записаны дифференциальные уравнения динамического равновесия его перемещающихся элементов для каждой степени свободы:
где:
Х1 и Х2 — текущие значения координат перемещений подвижных элементов КУС;
Р1 — давление рабочего тела на входе в КУС;
Р2 — давление рабочего тела на выходе КУС;
mi — массы подвижных элементов КУС;
Cпрi — коэффициенты, характеризующие жесткость пружин;
δпрi — численные значения упругой деформации пружин;
Dп и Dk1 — диаметры подвижных элементов КУС;
Y и П параметры, отражающие соотношения силовых и кинематических параметров элементов КУС, в процессе его функционирования.
Для нахождения числовых значений параметров Y и П, учитывающих соотношения силовых и кинематических параметров элементов крана, было составлено неравенство, вида:
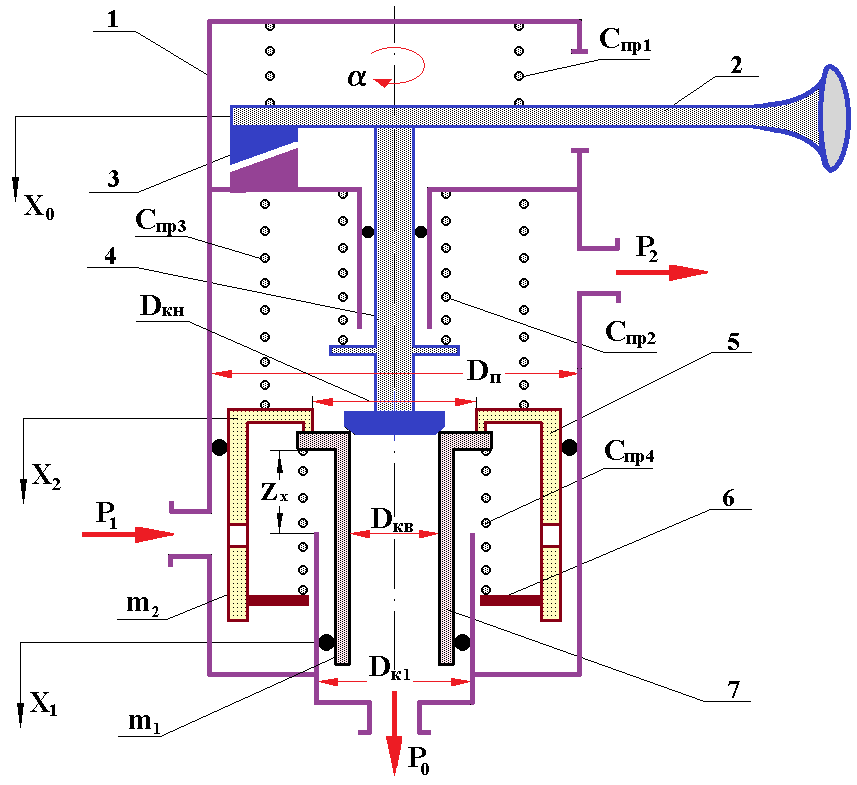
Рисунок 1 - Расчетная схема крана управления стояночной тормозной системой
Примечание: 1 – корпус краном КУС; 2 – рукоятка управления краном КУС; 3 – кулачки с заданным профилем; 4 – шток; 5 – следящий поршень; 6 – опорное кольцо; 7 – малый поршень
В выражениях (2) присутствуют силы трения Fтр, которые действуют между движущимися деталями КУС, которые значительно и негативно влияют на протекание рабочих процессов в КУС , , , . Испытание и контроль технического состояния аппаратов типа КУС целесообразно выполнять на основе анализа динамических зависимостей вида Р2=f(a), с учетом влияния всех силовых, конструктивных и геометрических и внешних факторов.
Конструкция КУС выполнена так, что зависимость координаты Х0, перемещения штока клапана 4, от угла поворота рукоятки 2, образует два линейных участка с перегибом в точке a = 10о , , . Поэтому, для расчета текущих значений координаты Х0(a) весь диапазон изменения угла поворота 0o £ a £ 90о был разбит на два неравных участка. Для каждого участка составлены уравнения вида:
Для вывода уравнений газовой динамики представим КУС, в составе экспериментальной исследовательской установки , в виде эквивалентной расчетной схемы (рис. 2). Подачу рабочего тела в КУС представим в виде процесса его наполнения через дроссель с пропускным сечением S1 и коэффициентом расхода μ1. Примем допущение о том, что компрессор обеспечивает стабильное давление Р1 на входе в КУС в любой момент времени .
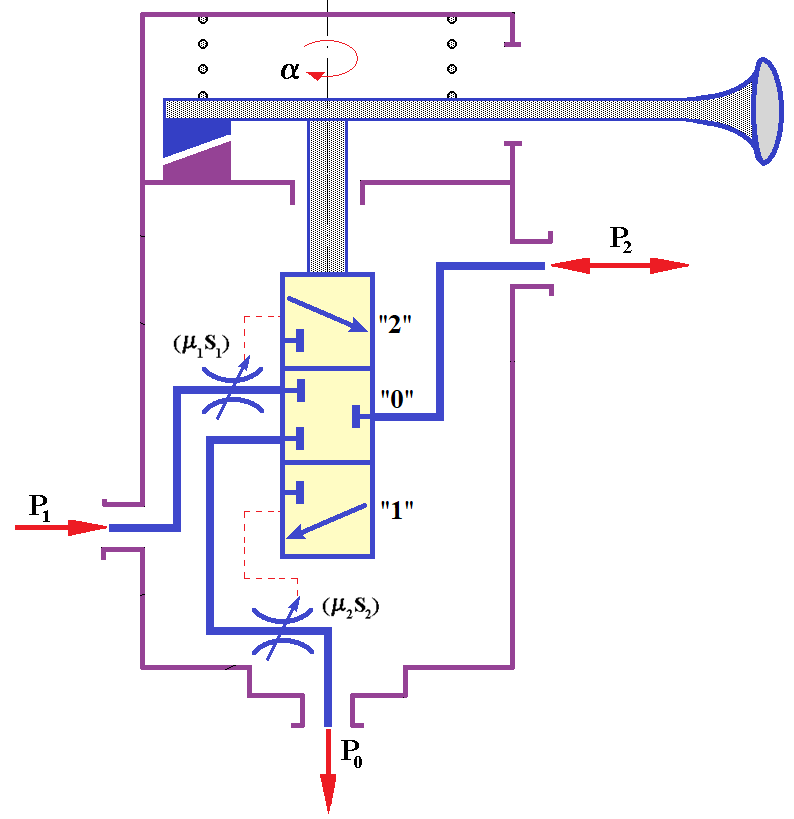
Рисунок 2 - Схема для расчета газодинамических процессов крана управления стояночной тормозной системой
Таким образом, с учетом вышеизложенного была разработана расчетная схема (см. рис. 2) для математического описания газодинамических процессов крана управления стояночной тормозной системой.
При составлении дифференциальных уравнений приемный учитывали, что в процессе испытаний, проходящий через КУС сжатый воздух наполняет ресивер (на рис. 2 не показан), который имеет емкость Vп . Обозначим атмосферное давление на выходе КУС как Р0 и составим дифференциальные уравнения расхода рабочего тела через клапан опорожнения (затормаживание):
а также через клапан наполнения (растормаживание):
Уравнения опорожнения и наполнения приемной емкости Vп, в процессе испытаний КУС, составлены с учетом обратной логики его функционирования, а также сочетаний координат положения клапана и поршня Х1 и Х2, возможных в процессе его функционирования, на основании баланса мгновенного массового расхода рабочего тела:
где Z — ход клапана в поршне на величину его рабочего зазора.
Параметры, входящие в состав уравнений (4), (5) и (6), рассчитываются с использованием приведенных ниже уравнений газодинамических процессов, в режимах наполнения и опорожнения КУС рабочим телом.
При постоянной величине входного давления, мгновенный массовый расход газа через местное сопротивление (регулируемый дроссель) описан выражением вида:
где:
μ — коэффициент расхода, представляющий произведение коэффициента, учитывающего потери на трение, и коэффициента, учитывающего уменьшение поперечного сечения струи при истечении;
S — площадь поперечного сечения отверстия дросселя, м2;
νкр=√kRT — критическая скорость, м/с;
Р0 — давление сжатого воздуха перед дросселем;
k = 1,4 — показатель адиабаты;
Т — абсолютная температура воздуха перед дросселем, К;
R = 287,14 м2/(c2×К) — универсальная газовая постоянная;
Параметр
Широкое применение для выполнения практических расчетов динамики сложных многоконтурных пневматических тормозных приводов автомобилей, получила гиперболическая функция
где:
В — параметр, который определяется как частное от деления времени опорожнения tо и времени наполнения tн пневмоаппарата рабочим телом через дроссель на величину 90 % от максимального значения давления .
Первый член выражения (9) определяет форму гиперболы и его принято обозначать символом А :
Запишем уравнение состояния газа в емкости пневмоаппарата, пренебрегая теплообменом между рабочим телом и окружающей средой :
где:
V — объем полости;
Р — давление газа в этой полости;
k = 1,4.
Величину параметра А вычисляли согласно уравнению (10). Расчет параметров
для режима наполнения, и
для режима опорожнения,
где:
Рвх и РV — значения давлений рабочего тела на входе в клапан аппарата КУС и за ним;
μ0i и μoj — коэффициенты расхода, которые определяли для каждого клапана по методике ;
Кμ1 и Кμ2 — коэффициенты, отражающие изменение коэффициентов μ0i и μoj при наполнении и опорожнении КУС;
V — объем приемной емкости, м3.
Программа расчета динамических процессов функционирования КУС предусматривает выполнение расчетов с использованием уравнений (1) – (11) с определением площади поперечного сечения клапана Ski при переменных значениях координат Х0 – Х2, перемещения подвижных элементов:
Представленная математическая модель, позволяет расчетными методами получать и исследовать фазовые динамические характеристики крана управления стояночным тормозом. Она учитывает изменения его геометрических, кинематических и силовых параметров, а также параметров его технического состояния.
3. Результаты исследований
В процессе экспериментальных исследований динамических характеристик КУС, его вход подключали к пневматическому блоку компьютерного диагностического комплекса, а выход соединяли с приемным ресивером объемом 1,5×10-3 м3. В соответствие с методикой, описанной в , на компьютерном испытательном комплексе ИРНИТУ были получены экспериментальные динамические характеристики в виде зависимостей давления на выходе КУС и угла поворота его органа управления от времени, которые приведены на рис. 3.
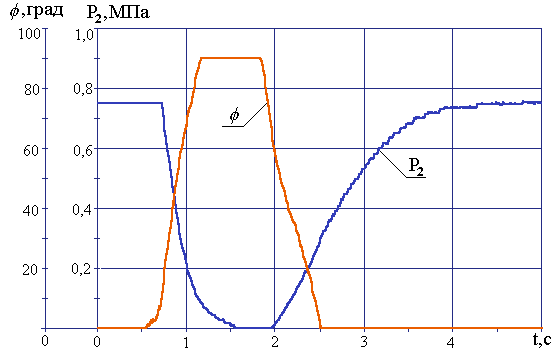
Рисунок 3 - Графики зависимости давления Р2 на и выходе КУС ПТП КамАЗ, и угла поворота φ органа его управления в динамике (эксперимент)
С использованием результатов эксперимента, были получены фазовые динамические характеристики КУС. Построение ФДХ КУС выполняли в среде Microsoft Exсel. Вид графика фазовой динамической характеристики КУС показан на рис. 4.
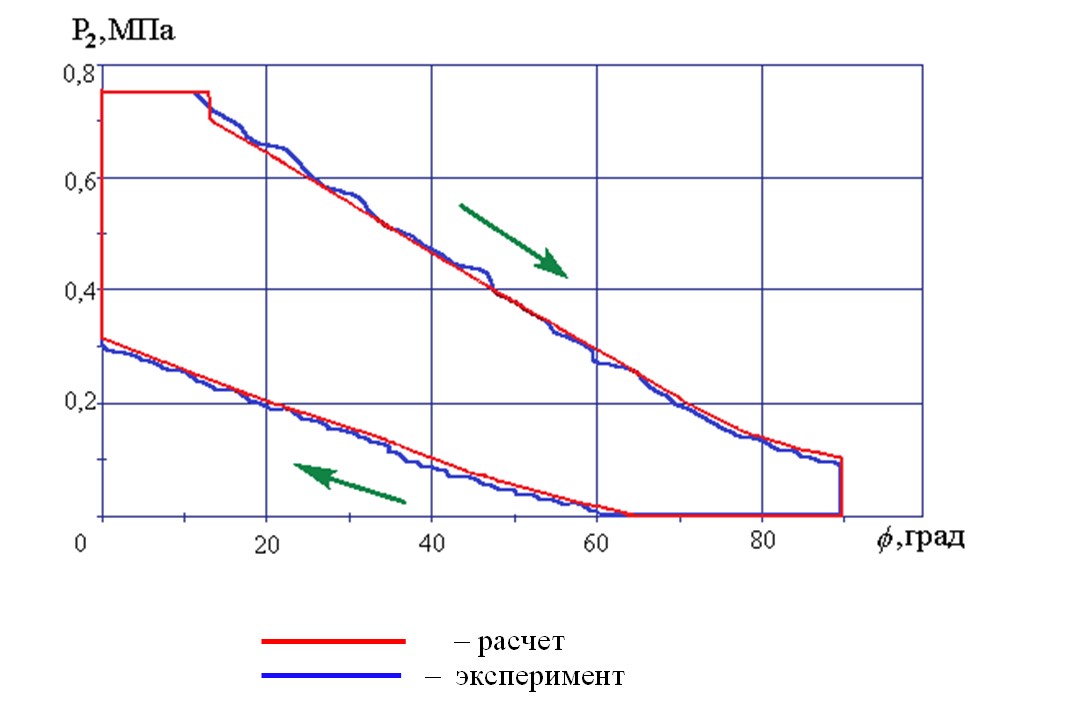
Рисунок 4 - Фазовая динамическая характеристика КУС
В процессе расчета динамических характеристик КУС были приняты следующие исходные параметры:
Рвх = 750000 Па;
Р0 = 0;
Vп = 1,5×10-3 м3;
Dн = 3,8×10-2 м;
Dкн = 1,8×10-2 м;
Dкв = 9,0×10-3 м;
δпр1 = 20,6×10-3 м;
δпр1 = 2,5×10-3 м;
m1 = 2,5×10-2 кГ;
m2 = 3,5×10-2 кГ;
Спр3=50157 Н·м;
Спр4=2135 Н·м;
δпр3 = 0;
δпр4 = 3,1×10-2 м.
Обозначения этих параметров КУС приведены в соответствии с расчетными схемами (рис. 1 и рис. 2).
В процессе оценки адекватности математической модели КУС были выполнены расчеты динамических процессов его функционирования, результаты которых сравнивали с полученными его экспериментальными динамическими характеристиками (рис. 3). Затем результаты расчетов и эксперимента были представлены в виде фазовых динамических характеристик (зависимостей давления Р2 на выходе КУС от управляющего воздействия — угла φ), вид которых представлен на рис. 4. Взаимное наложение результатов расчета динамических процессов на математической модели и результатов экспериментальных исследований наглядно показывает, насколько близко они совпадают как по величине, так и по форме.
Анализ надежности аппаратов ПТП автомобилей и влияющих на нее факторов , показывает, что на форму их ФДХ влияют не только геометрические, кинематические и силовые параметры, и параметры технического состояния, но и в значительной степени влияют и режимы их работы. Следовательно, в процессе испытаний КУС следует обеспечивать высокую стабильность тестовых воздействий , , . Это позволит исключить негативное влияние нестабильности тестовых воздействий на результаты испытаний и контроля технического состояния КУС.
4. Обсуждение результатов
На заключительном этапе, были выполнены статистические расчеты, которые позволили количественно оценить результаты оценки адекватности разработанной математической модели. Для этого были определены параметры, характеризующие различие между экспериментальными динамическими характеристиками и рассчитанными на ЭВМ по линейному и среднеквадратичному критериям с доверительной вероятностью 0,95. В итоге было установлено, что данные различия являются несущественными, поскольку выполняется неравенство:
Также было выполнено сравнение средних. При этом установлено, что:
5. Заключение
В процессе проведенного исследования установлено, что разработанная математическая модель является адекватной и позволяет расчетным методом выполнять анализ динамических процессов функционирования крана управления стояночной тормозной системой автомобиля с учетом его геометрических, кинематических, силовых параметров и газодинамических процессов.
Разработанная математическая модель, позволяет расчетными методами получать и исследовать фазовые динамические характеристики крана управления стояночным тормозом. Она позволяет разработчикам аппаратов пневматического тормозного привода оптимизировать конструкцию аппаратов с обратной логикой, с учетом вариации его геометрических, кинематических и силовых параметров, а специалистам в области эксплуатации, разрабатывать методы неразрушающего контроля параметров их технического состояния , , , , что особенно важно в условиях необходимости импортозамещения в связи с недоступностью производителя пневмоаппаратов — фирмы Wabco.
