РЕАЛИЗАЦИЯ МЕТОДА СОПРЯЖЕННЫХ ГРАДИЕНТОВ НА ГРАФИЧЕСКОМ ПРОЦЕССОРЕ С ПРИМЕНЕНИЕМ МАТРИЧНЫХ МЕТОДОВ РЕШЕНИЯ СЛАУ
РЕАЛИЗАЦИЯ МЕТОДА СОПРЯЖЕННЫХ ГРАДИЕНТОВ НА ГРАФИЧЕСКОМ ПРОЦЕССОРЕ С ПРИМЕНЕНИЕМ МАТРИЧНЫХ МЕТОДОВ РЕШЕНИЯ СЛАУ
Аннотация
В работе представлен алгоритм решения систем линейных алгебраических уравнений (СЛАУ) методом сопряженных градиентов на графическом процессоре. В качестве основного инструмента реализации предложен класс-контейнер для работы с матрицами на базе технологии NVIDIA CUDA. Производительность решения СЛАУ методами Крамера и сопряженных градиентов была сопоставлена на центральном и графическом процессорах. Результаты исследования показали, что распараллеленный метод сопряженных градиентов, выполненный на графическом процессоре, обладает наибольшей эффективностью при обработке СЛАУ с симметричной положительно определенной основной матрицей. Рассматриваемый подход к параллельной обработке матричных операций имеет потенциал для применения в различных областях, где требуется решение крупных систем уравнений, таких как в науке, инженерии и финансах. В целом, данная работа представляет практическую значимость в области оптимизации производительности вычислений и закладывает фундамент для решения многих математических задач на графическом процессоре.
1. Введение
Системы линейных алгебраических уравнений (СЛАУ) являются фундаментом задач для многих областей естествознания, включая механику, электротехнику, экономику и компьютерную графику. Способы решения СЛАУ имеют важное значение, особенно при обработке большого количества уравнений. Методы решения СЛАУ делятся на точные и приближенные, включая итерационные методы. Алгоритмы для вычислительных машин, основанные на точных методах, таких как метод Гаусса и метод Крамера, подходят для систем порядка не выше 20, в то время как итерационные методы могут обрабатывать системы более высокого порядка.
Одним из подходов к решению СЛАУ является параллельное программирование, включая использование графических процессоров (GPU). В отличие от центрального процессора (CPU), GPU имеет сотни или тысячи ядер, способных обрабатывать вычисления одновременно. Это делает GPU более эффективным для параллельных задач, таких как обработка графики, научные вычисления и машинное обучение. Кроме того, на GPU реализуются различные методы решения СЛАУ.
Метод сопряженных градиентов относится к итерационным методам и основывается на умножении матриц и вычислении скалярных произведений векторов. Умножение матриц строится на основе нахождения суммы произведений соответствующих элементов исходных матриц, т. е. состоит из множества несвязных вычислений. Поэтому метод сопряженных градиентов подходит для распараллеливания на графическом процессоре.
2. Работа с матрицами при использовании технологии CUDA
Архитектура CUDA представляет собой специальный набор инструментов и библиотек, предназначенный для программирования графических процессоров. В качестве языков программирования CUDA поддерживает Python, C, C++ и т. д. Распараллеливание вычислений на GPU достигается за счет запуска большого количества потоков. Потоки в архитектуре CUDA представляются в виде сложной структуры. На верхнем уровне располагается сетка, которая является дискретным трехмерным пространством блоков, каждый блок в свою очередь трехмерным пространством потоков.
Матрицы заданного размера, состоящие из действительных чисел, образуют следующее линейное пространство:
В настоящей работе матрицы представляли как одномерные динамические массивы. Доступ к элементу матрицы осуществляли по следующему соотношению: , где N – число строк в матрице, M – число столбцов в матрице, ptr – указатель на первый элемент массива. В качестве «обертки» для динамического массива использовали класс-контейнер devMatrix.
Таблица 1 - Основные методы класса devMatrix
3. Сложение матриц на GPU
В качестве иллюстрации внутреннего устройства класса devMatrix и работы CUDA, рассмотрим перегрузку оператора «+». Данный оператор осуществляет сложение двух матриц. Под сложением матриц будем понимать следующую операцию:
При использовании CUDA, сумма каждой пары элементов (aij, bij) вычисляется в отдельном потоке. В данном случае использовали двумерное представление сетки и блока, при этом число блоков в одном из измерений вычисляли как ближайшее целое, большее или равное числу . Блоки имели размер 32 × 32 потока. Каждый поток обрабатывал одну сумму (см. рис. 1).
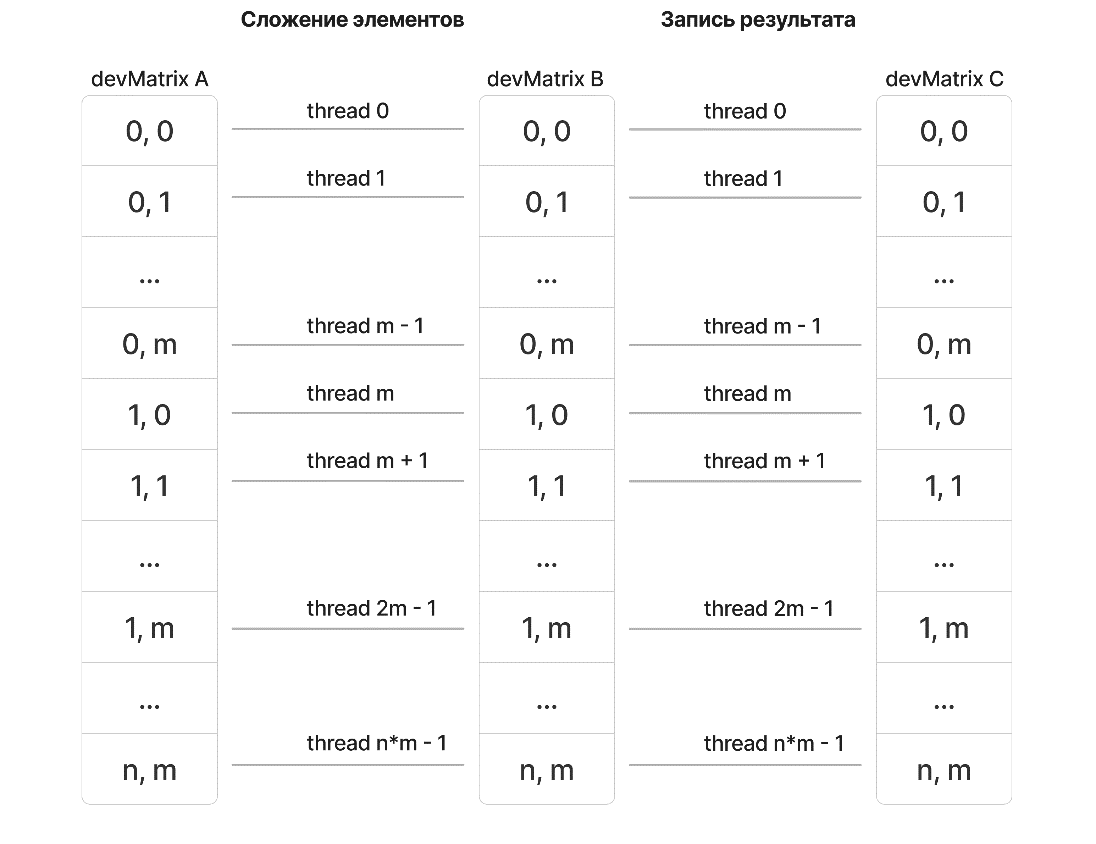
Рисунок 1 - Блок-схема суммы матриц
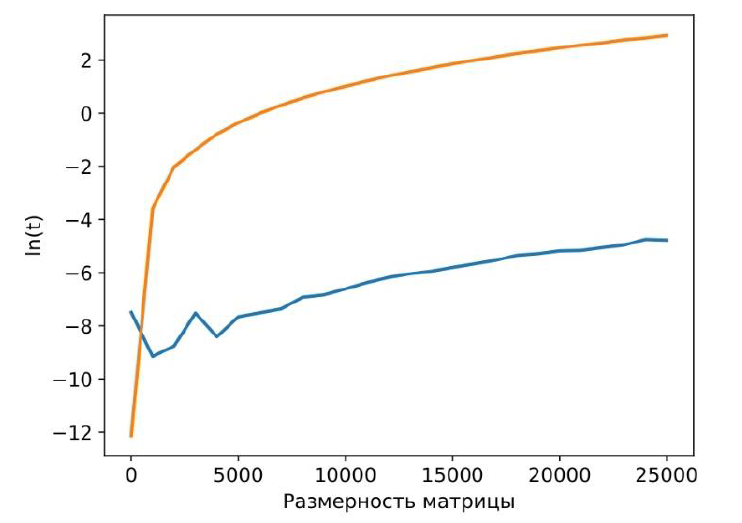
Рисунок 2 - Сравнение производительности сложения матриц на CPU и GPU
Примечание: оранжевая и синяя линии отображают зависимость времени от размерности матрицы для операции сложения в логарифмических координатах на CPU и GPU соответственно
Для корректной работы, стоит учитывать, что в какой-то момент времени будет как минимум два объекта типа devMatrix, при условии, что поддерживается перемещающий конструктор. Идеология перемещающих конструктора и оператора играют важную роль в ОПП реализации матричных операций. При манипуляции большими объемами данных стоит избегать их дублирования, которое возникает при инициализации или переопределении в результате возвращения из функции rvalue объектов. В противном случае минимальное количество объектов при обработке операции возрастает до трех, что соответствует (в случае квадратной матрицы порядка 25000) 13.98 ГБ. Если отбросить ограничения, связанные с памятью, на современных видеокартах на размерность сетки накладывается ограничение в максимальное число блоков, что соответствует максимальной размерности первого измерения. Максимальная размерность блока составляет 1024 потока (подробные данные см. гайд ссылка на гайд).
Таким образом максимальное количество строк/столбцов в квадратной матрице определяется следующим образом:
с учетом что в нашей реализации
должно быть кратно
что во много раз превышает лимит памяти.
В результате верхнюю границу размеров матрицы определяет именно объем глобальной память GPU.
4. Умножение матриц на GPU
Умножение матриц в алгебраической форме записывается следующим образом:
Классический распараллеленный алгоритм произведения матрицы схож с суммированием, но для каждого элемента отдельно запускается цикл, в котором рассчитывается сумма произведений (см. рис. 3). Важно, чтобы промежуточные значения суммы хранились в быстрой регистровой памяти GPU, иначе произойдет падение производительности программы.
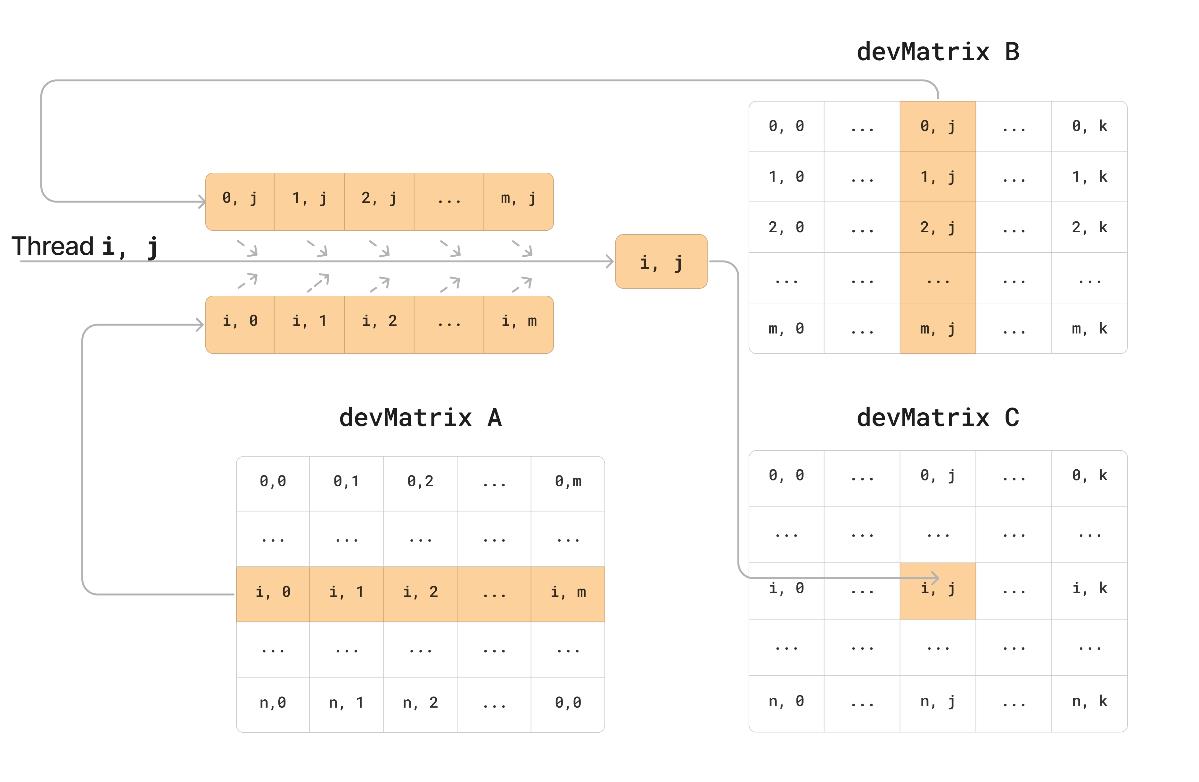
Рисунок 3 - Блок-схема произведения матриц
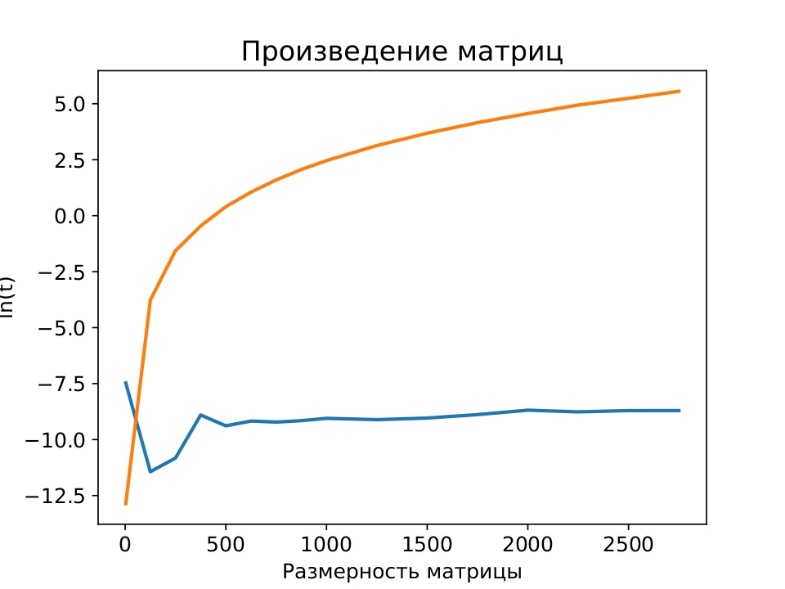
Рисунок 4 - Сравнение производительности умножения матриц на CPU и GPU
Примечание: оранжевая и синяя линии отображают зависимость времени от размерности матрицы для операции умножения в логарифмических координатах на CPU и GPU соответственно
Представленный алгоритм является самой простой реализацией параллельного произведения. Существуют альтернативные алгоритмы:
1. Распараллеливание не только вычисления отдельного элемента результирующей матрицы, но и отдельных произведений соответствующей суммы, за счет третьего измерения z в сетке. У данного алгоритма есть две глобальные проблемы. Первая заключается в гонке потоков на запись произведений, появляется она из-за того, что мы вынуждены обращаться не к регистровой памяти, а к глобальной. Причем в подобной реализации в сочетание с нашим представлением класса devMatrix за суммирование произведений одного элемента не всегда отвечает одни блок, поэтому накладывается ограничение на использование разделяемой памяти. Вторая проблема связана с резким уменьшением максимальной размерности матриц из-за уменьшения числа блоков в x, y измерении из-за добавления z измерения:
2. Рассматривать сетку в двух измерениях соответствуя элементам результирующей матрицы. В каждом блоке будет происходить распараллеленное вычисление суммы произведений с использованием разделяемой памяти. Данный алгоритм позволит вычислять произведения матриц с самой высокой скоростью, но если будет происходить перемножение матриц , то максимальное значение k (число столбцов матрицы A, число строк матрицы B) равно 1024, из-за ограничения на число потоков внутри блока.
По сравнению с указанными альтернативами, классический (простой) алгоритм предпочтителен, он обеспечивает хорошую скорость около граничной области размерности матриц по памяти.
5. Метод сопряженных градиентов
Пусть система из n линейных алгебраических уравнений c n неизвестными представлена в матричной форме:
где – основная матрица системы,
– столбец неизвестных,
– столбец свободных членов.
Метод сопряженных градиентов, подразумевает, что основная матрица системы A – симметрична и положительно определена, т. е. .
Для решения такой системы методом сопряженных градиентов можно использовать следующее рекуррентное соотношение:
Шаг 0:
– произвольный вектор.
Шаг индукции
Отметим, что метод сопряженных градиентов всегда сходится к решению исходной СЛАУ за итераций (
– порядок системы).
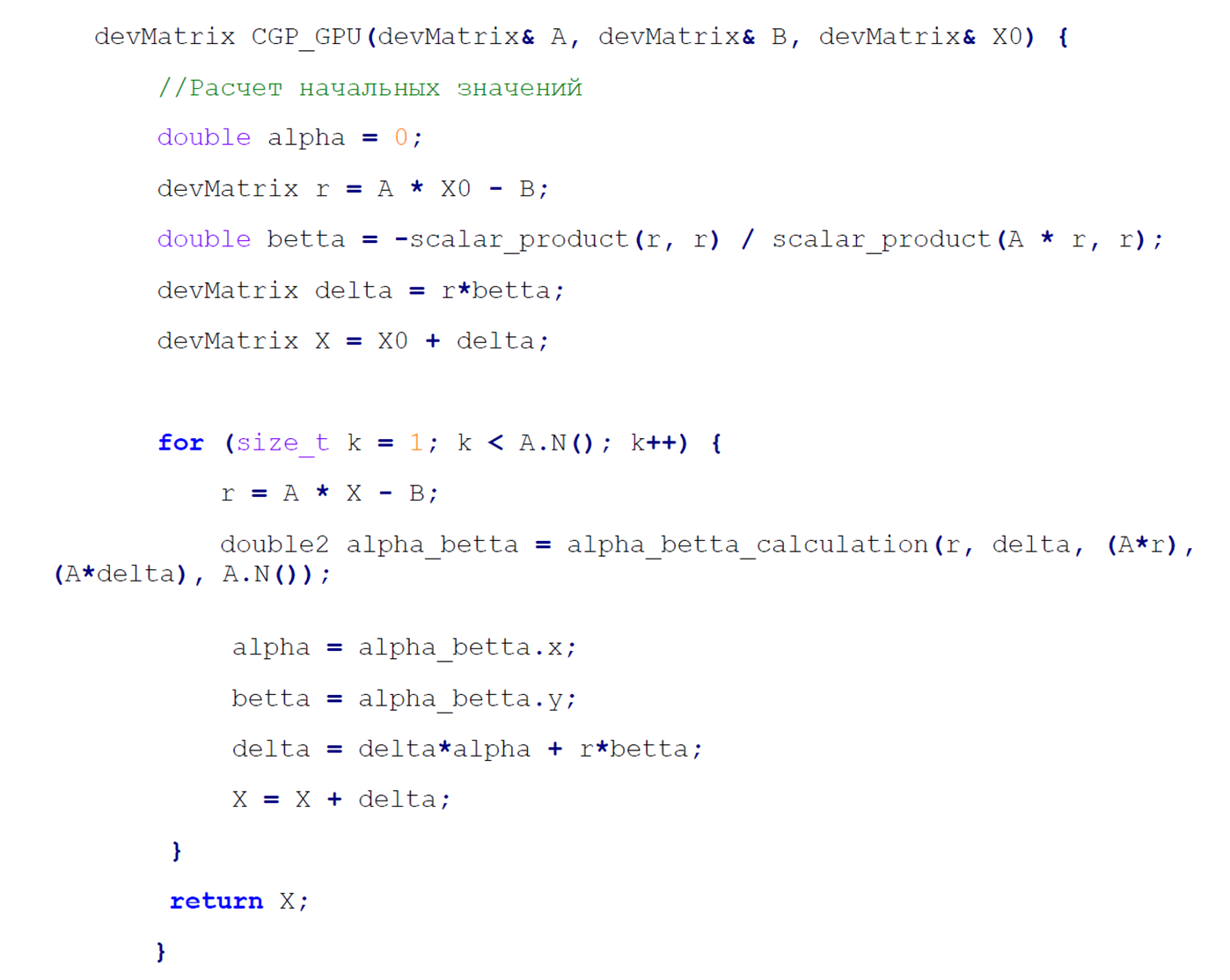
Рисунок 5 - Вид итогового алгоритма с учетом построенных инструментов для работы с матрицами
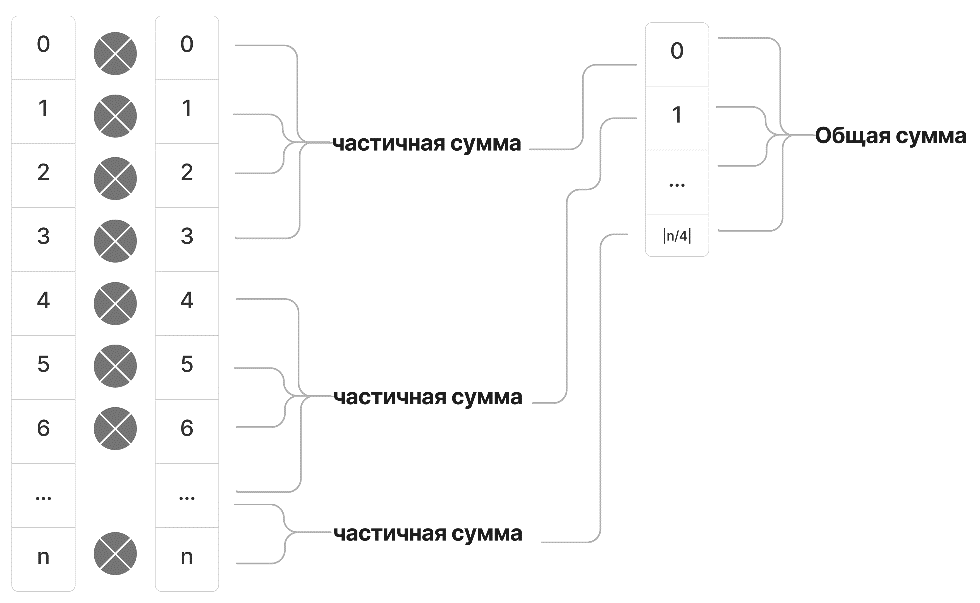
Рисунок 6 - Блок-схема реализации скалярного произведения
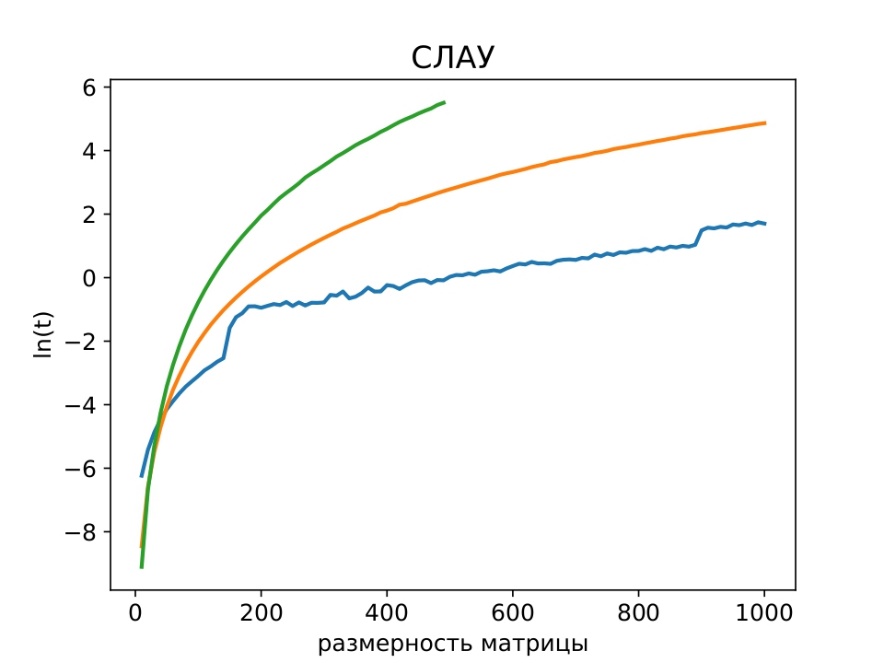
Рисунок 7 - Метод Крамера, спряжённых градиентов на CPU и GPU
Примечание: зеленая, оранжевая и синяя линии отображают зависимость времени от размерности основной матрицы системы при решении СЛАУ в логарифмических координатах на CPU методом Крамера и МСГ и МСГ на GPU соответственно
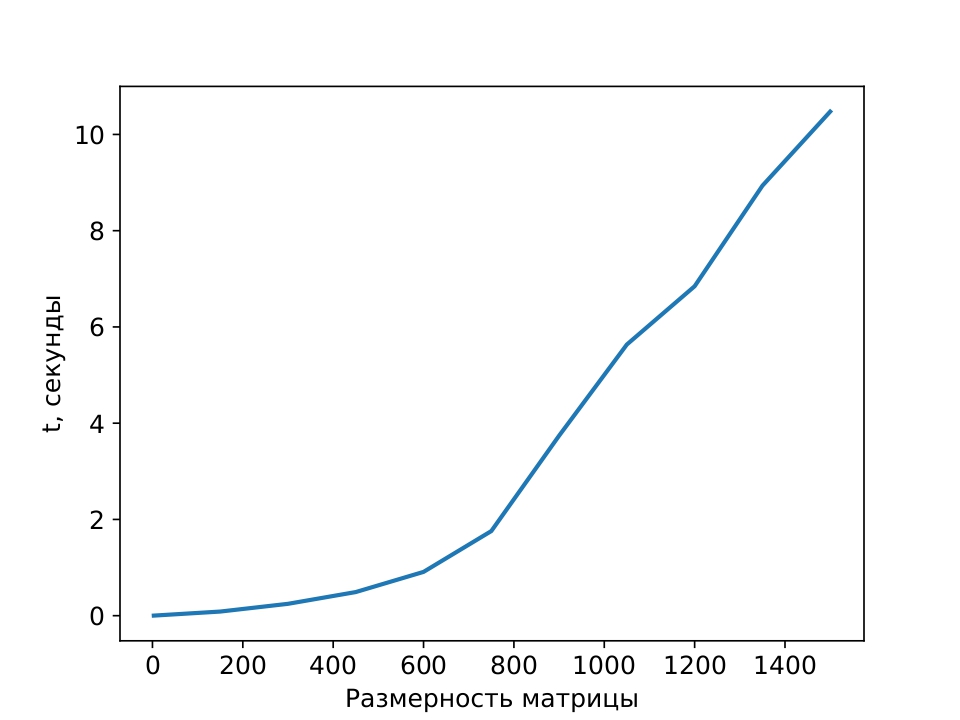
Рисунок 8 - Метод спряжённых градиентов на GPU
Примечание: зависимость времени от размерности основной матрицы системы при решении СЛАУ методом МСГ на GPU
Все тесты проводились на следующей конфигурации:
Процессор: AMD Ryzen 5 5600 6-Core Processor 3.50 GHz;
Оперативная память: 16,0 ГБ;
Графический процессор: GeForce RTX 3060 12,0 ГБ, 3584 ядер CUDA.
6. Заключение
В настоящей работе предложены основные инструменты для обработки матричных операций с использованием технологии CUDA. На примере сложения и умножения матриц показано, что алгоритмы, построенные на распараллеливании вычислений, работают на несколько порядков эффективнее аналогичных последовательных программ на CPU. Определены границы размерностей матриц, которые можно обработать на GPU.
На основе библиотеки devMatrix, построен алгоритм решения СЛАУ методом сопряженных градиентов, который превзошел аналогичный алгоритм на CPU и метод Крамера по скорости решения. Полученный результат демонстрирует актуальность технологии CUDA в контексте научных расчетов, а также предоставляет возможность написания простых, но в то же время эффективных матричных алгоритмов на базе библиотеки devMatrix.
