Сравнительный анализ алгоритмов построения оптимального маршрута полета летательного аппарата при наличии зон угроз
Сравнительный анализ алгоритмов построения оптимального маршрута полета летательного аппарата при наличии зон угроз
Аннотация
В статье рассматриваются эффективные алгоритмы поиска оптимального маршрута полета летательного аппарата при наличии зон угроз и неопределенностей. На данный момент в теории насчитывается огромное количество алгоритмов поиска кратчайшего пути, которые активно используются для построения оптимальных маршрутов летательных аппаратов с целью достижения ими заданного пункта назначения. Проведен сравнительный анализ двух исследуемых методов: А* (звезда) и алгоритма Дейкстры. Работа алгоритмов сравнивается по двум критериям: длина найденного кратчайшего пути и количество шагов его нахождения. Результаты сравнения представлены в аналитическом и графическом виде. На основании проведенных расчетов были сделаны выводы о достоинствах рассмотренных методов и области их применения.
1. Введение
В настоящее время проектирование маршрутов для беспилотных летательных аппаратов (БПЛА) в детерминированной и стохастической системах является актуальной задачей, поскольку данные аппараты применяются в различных областях деятельности, в особенности в оборонной промышленности государств, а также в гражданской сфере, в частности, при ликвидации последствий чрезвычайных ситуаций.
БПЛА представляет собой безэкипажный летательный аппарат, управление перемещением которого в воздушном пространстве происходит благодаря наличию компьютера и программного обеспечения . Управление БПЛА происходит как автономно, так и с помощью централизованного управления оператором, который имеет возможность корректировать маршрут полета дистанционно в случае необходимости.
Отсутствие летчика на борту дает следующие преимущества:
- нет необходимости в системах, связанных с жизнеобеспечением экипажа, что позволяет сделать аппарат более простым и дешевым;
- исчезают ограничения на максимальные значения перегрузок, угловых скоростей и их градиентов, что расширяет возможности аппарата;
- значительно снижается влияние психофизических факторов на результат
- возможен высокий относительный вес полезной нагрузки;
- более высокая степень готовности и мобильности;
- возможность управления БПЛА с безопасной удалённой территории , .
Для решения задачи построения траектории движения с успешным обходом препятствий применяются различные алгоритмы.
Для планирования пути БПЛА применяют алгоритмы на графах, оптимизационные методы, стохастические алгоритмы .
В современных условиях большую роль приобретают алгоритмы, учитывающие различные уровни информированности:
· алгоритм слепого поиска или алгоритм поиска без графа информации:
o поиск в глубину;
o поиск в ширину;
o алгоритм Дейкстры;
· алгоритм эвристического поиска или алгоритм поиска по информативному графу:
o «жадный алгоритм»;
o алгоритм А* (А-звезда).
Графом G (V, E), см. (1), называется совокупность двух множеств — непустого множества V (множества вершинv) и множества Е двухэлементных подмножеств множества V (Е — множество рёберe), т.е. :
где: V – непустое множество (множества вершин v);
E – множество двухэлементных подмножеств множества V (Е — множество рёбер e);
v,e – элементы графа (вершины и рёбра).
Слепой поиск отличается тем, что для работы алгоритма не требуется дополнительная информация, позволяющая упорядочивать выбор в узлах так, чтобы наилучшие варианты рассматривались в первую очередь.
Методы неинформированного (слепого) поиска в большинстве случаев неэффективны, поэтому возникает необходимость применения алгоритмов эвристического поиска.
Информация о конкретной задаче формулируется в виде эвристической функции. Эвристическая функция на каждом шаге перебора оценивает альтернативы, ссылаясь на дополнительную информацию с целью принятия решения о том, в каком направлении следует продолжать перебор .
Эвристическая оценочная функция может иметь зависимость как от внутренних свойств оцениваемого состояния (т.е. свойств, входящих в описание состояния элементов), так и от характеристик всего пространства состояний.
В ряде ситуаций эвристика сокращает перебор начальных и целевых состояний для одних задач, в то время как для других не уменьшает перебор (тогда поиск решения может происходить даже дольше, чем с использованием неинформированного поиска), либо не обеспечивает нахождение оптимального маршрута .
2. Постановка задачи
Имеется полетная карта, заданная в горизонтальной плоскости в виде взвешенного ориентированного графа G (V, E), без дуг отрицательного веса двух уровней информативности:
- информативный граф (детерминированная среда);
- граф без информации (стохастическая среда со статическими препятствиями).
Потребные значения высоты полета БПЛА задаются в узлах маршрута, карта высот формируется отдельно.
В случае динамически меняющейся обстановки в пространстве применяется вероятностный метод, который состоит в случайном выборе точек, распределенных с заданной вероятностью в пространстве. Распределение производится во всем пространстве, включая препятствия; при таком подходе точки, попавшие на препятствия, исключаются. При этом могут возникнуть ситуации, когда случайный выбор маршрутных точек влечет за собой неоптимальный маршрут пути БПЛА .
Требование задачи состоит в поиске наиболее оптимального пути по двум критериям: длина пути и шаг его определения.
3. Алгоритмы, применяемые для поиска кратчайшего пути
3.1 Алгоритм Дейкстры
Алгоритм Дейкстры — алгоритм на графах, созданный в 1959 году нидерландским учёным Эдсгером Дейкстрой. Данный метод позволяет найти кратчайшие пути от одной из вершин графа до всех остальных или до заданной.
Особенность рассматриваемого алгоритма — он применяется только для графов с рёбрами неотрицательного веса .
Алгоритм Дейкстры обходит каждую вершину в графе по возрастанию расстояния, начиная от стартовой, то есть вершины будут просматриваться постепенно с возрастанием радиуса вокруг начальной точки .
Эффективность алгоритма доказана в исследовании индонезийских ученых , однако это также подтверждает недостаток алгоритма – медленный поиск заданной точки.
3.2 Алгоритм А* (А-звезда)
Алгоритм А* (А-звезда) является улучшенной модификацией алгоритма Дейкстры. Это алгоритм поиска по первому наилучшему совпадению на графе, который находит маршрут с наименьшей стоимостью от начальной вершины к целевой. Данный алгоритм можно оптимизировать для практического применения в реальных условиях при ряде ограничений объектов (максимальная скорость, минимальный радиус поворота и т. д.) .
Метод А-звезда относится к экспоненциальной категории алгоритмов, в которых поиск происходит по всему множеству исследованных альтернатив, а именно все найденные вершины графа содержатся в списках, и выбор происходит на основе критерия ранжирования, который будет учитывать эффективность продолжения поиска через эти вершины на основе числовой характеристики .
Стоимость перемещения для алгоритма А* рассчитывается с помощью выражения:
где: h(x) – эвристическая функция, позволяющая оценить путь до цели на каждом шаге;
g(x) – расстояние от начальной точки до целевой.
В качестве эвристической функции при двумерной таблице с 8-ю направлениями принято использовать расстояние Чебышева (максимальное значением абсолютного значения разности между горизонтальной и вертикальной координатами между двумя точками), т.е.:
где: n – рассматриваемая клетка; xn, yn – координаты рассматриваемой клетки; xgoal, ygoal – координаты целевой клетки.
Если в формуле (2) h(x) = 0, то метод А* превращается в алгоритм Дейкстры. Тем не менее алгоритм А* может привести к неоптимальному решению задачи, поскольку он ищет путь целенаправленно к одной точке, осматривая только соседние от неё.
4. Сравнительный анализ представленных алгоритмов
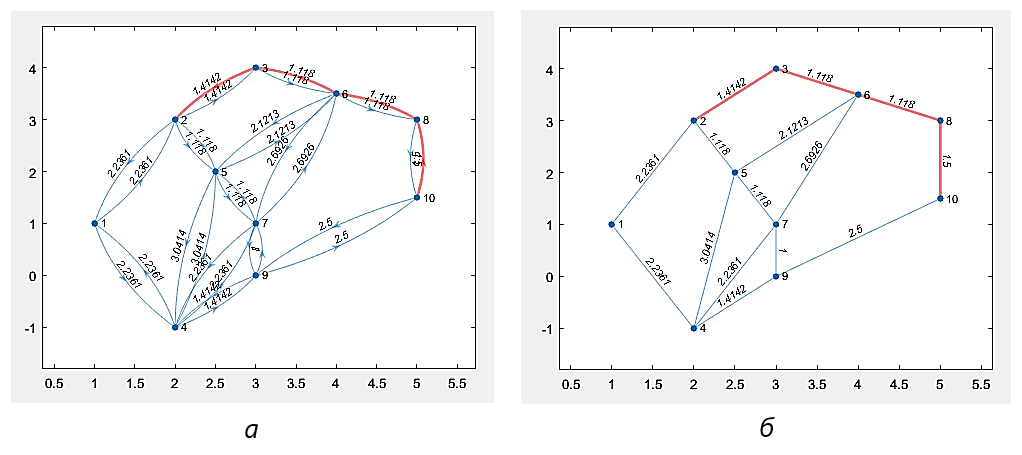
Рисунок 1 - Поиск маршрута:
а – метод Дейкстры; б – метод А*
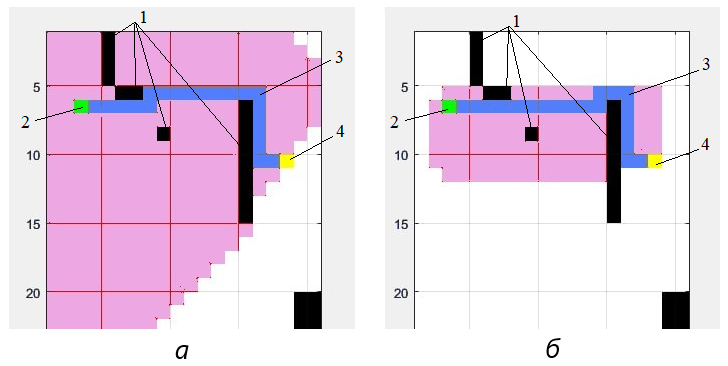
Рисунок 2 - Карта маршрутов:
а – метод Дейкстры; б – метод А*; 1 – препятствия; 2 – начальная точка; 3 – путь; 4 – целевая точка
Таблица 1 - Результаты
Алгоритм | Алгоритм Дейкстры | Алгоритм А* |
Количество шагов алгоритма | 348 | 104 |
5. Заключение
На основании проведенных расчетов были сделаны выводы о достоинствах рассмотренных методов и области их применения.
Полученные результаты сравнительного анализа методов А* (звезда) и Дейкстры (см. Таблицу 1) показали, что алгоритм А* (звезда) является более точным и быстрым методом поиска оптимального пути, чем алгоритм Дейкстры.
Однако применение алгоритма А* (звезда) считается наиболее эффективным в условиях, когда известно точное местоположение цели. Но в этом и его недостаток – алгоритм не всегда оптимален, поскольку двигается только в заданную точку, рассматривая соседние, тогда как алгоритм Дейкстры обходит каждую вершину графа, увеличивая радиус поиска.
На основании проведенного анализа , , можно сделать вывод о том, что эвристические методы поиска не всегда гарантируют нахождение наилучшего решения, поскольку возможен так называемый «пропуск цели». В указанных ситуациях предпочтительно использование «классических» алгоритмов на графах.
Помимо рассмотренных алгоритмов, применяемых для поиска маршрутов в стохастических системах, также имеет место использование алгоритма D* (звезда), который является модификацией вышеописанных поисковых методик .
Исследование и разработка алгоритмов поиска оптимального маршрута пути БПЛА имеет большую практическую ценность, как для гражданской, так и для военной авиации, поэтому является перспективным направлением развития науки и техники.
