Проблема оценки эффективности теста Миллера-Рабина
Проблема оценки эффективности теста Миллера-Рабина
Аннотация
В данной работе проведён анализ эффективности теста Миллера-Рабина. В качестве отправной точки для анализа был выбран алгоритм поиска последовательности чисел ψn. В рамках данного алгоритма было обнаружено «бутылочное горлышко» и представлен способ его решения. Им оказался расход памяти.
Основной идеей выступает распределение простых чисел по значениям bin(ordp(ai)). Сделан вывод о неравномерности распределения и сильном смещении к меньшим значениям bin(ordp(ai)). Для наглядности все рассуждения и результаты экспериментов сопровождаются графиками.
Благодаря полученным данным был сделан вывод о возможном разбиении всего множества простых чисел на подмножества по значению bin(ordp(ai)). Таким образом, получен итоговый алгоритм, в котором оптимизирован расход памяти по сравнению с исходным.
1. Введение
Современная криптография, а особенно её защищённость, основывается на различных свойствах простых чисел. Поэтому возникает необходимость в эффективном поиске достаточно больших простых чисел. Существует множество различных подходов для решения данной проблемы. Однако наиболее известным и эффективным является использование теста Миллера-Рабина.
Таким образом, актуальность работы обеспечивается использованием простых чисел в современных исследованиях. Например, в статьях и представлен новый протокол маршрутизации, основанный на простых числах, позволяющий обнаруживать кротовые норы в мобильных сетях. Также в статьях , и представлен алгоритм шифрования, основанный на простых числах и биометрии, а также его применение в технологии блокчейна, а также его использование в интернете вещей. А в статье представлен алгоритм шифрования изображений, использующий множество простых чисел и полярное разложение.
Основной целью является исследование эффективности работы теста Миллера-Рабина и распределения его ошибки. Для достижения поставленной цели были сформулированы и решены следующие задачи:
1. Анализ существующих методов оценки эффективности теста Миллера-Рабина.
2. Анализ возможных оптимизаций для существующего метода оценки эффективности теста Миллера-Рабина.
Тест Миллера-Рабина , является вероятностным тестом. Это означает, что тест может выносить ошибочный вердикт, но с очень маленькой вероятностью. В настоящий момент известна только верхняя граница для её значения, однако она сильно завышена.
Есть и другой подход к оценке эффективности алгоритма – последовательность чисел – наименьшее строго псевдопростое число для n первых простых чисел. Главная сложность этого подхода – быстрый рост значение и отсутствие эффективных непереборных алгоритмов.
Таким образом, имея достаточно точную информацию об эффективности теста Миллера-Рабина, можно на его основе создавать модификации и получать достаточно точные асимптотики времени выполнения и памяти.
К примеру, К. Нари, Е. Оздемир и Н. А. Озкирисци представили алгоритм , добавляющий дополнительные проверки после запуска теста Миллера-Рабина с основанием 2. Также Д. Соренсон и Д. Вебстер разработали алгоритм по поиску наборов простых чисел по заданному паттерну . Для построения оценки эффективности они используют знания о распределении строго псевдопростых чисел.
2. Методы и принципы исследования
Тест Миллера-Рабина – вероятностный тест, представленный сперва Г. Миллером в 1976 г. , затем улучшенным М. О. Рабиным в 1980 . Основан этот тест на модификации теоремы Эйлера .
Для упрощения дальнейшего описания теорем и алгоритмов введём следующие функции:
Определение 1. Пусть n – произвольное натуральное число, представимое следующий вид:
Тогда функции bin(n) и odd(n) определяются следующим образом:
Тогда каждая итерация теста Миллера-Рабина заключается в выборе произвольного основания и проверки выполнимости следующих условий:
Если одно из условий выполнилось, то число a называется свидетелем простоты числа n, а само число считается прошедшим текущую итерацию теста.
Первый подход к оценке эффективности алгоритма основан на вычислении количества свидетелей простоты произвольного числа. Все вычисления, производимые в рамках данного подхода основаны на следующей теореме :
Теорема 1. Пусть n – произвольное натуральное число, представимое следующий вид:
Тогда выполняются все перечисленные условия:
Где за ordk(a) обозначают порядок числа a по модулю k.
Обозначим за W(n) – количество свидетелей простоты. Ш.Т. Ишмухаметов, Б.Г. Мубараков и Р.Г. Рубцова представили конечную формулу для расчёта функции W(n) для случая полупростого n=p*q:
Однако позже Б. Г. Мубараков получил формулу для произвольного числа n по его разложению на простые множители :
Следующим шагом для оценки эффективности вводится функция Fr(n) – вероятность выбора свидетеля простоты. Поскольку из условий (3) следует, что НОД (a, n)=1, то значение функции будет вычисляться по следующей формуле:
М.О. Рабин доказал, что ¼ – верхняя граница для Fr(n). Однако данное значение достигается для бесконечного количества чисел n, что значительно усложняет анализ этой функции.
Поэтому оценки вычислялись для среднего значения вероятности на отрезке Avg(Fr(n)). Первая оценка для этой функции была получена Б.Г. Мубараковым, но ограничиваясь только полупростыми числами n=p*q при фиксированном p:
Однако данная оценка была сильно завышена, поэтому Б.Г. Мубараков представил улучшение оценки, но для случая p=2*p', где p' – простое число. Для этой цели рассматривались два возможных случая отношений p и q:
1. q=(p-1)k+1 → в этом случае верхняя оценка из (5) становится асимптотикой функции .
2. q=2k+1, где 2k mod (p-1) ≠ 0 → в этом случае верхняя оценка из (5) улучшается до следующей :
Наконец, посчитав математическое ожидание от обоих вариантов получаем результат :
После чего было высказано предположение, что для всех значений p оценка будет принимать следующий вид :
Где коэффициент находится на отрезке
.
Также были получены результаты для трёхпростых чисел . Первая оценка была получена для фиксированных
и
:
Однако эта оценка также является сильно завышенной и требует улучшения. Одним из возможных способов разбиение всех чисел на группы, расчёт оценки для каждой группы и расчёт общего значения через математическое ожидание.
На настоящий момент получены оценки для двух классов:
1. Трёхпростое число, при фиксированном и
, удовлетворяющих следующим условиям:
Итоговая оценка для такой ситуации , :
2. Трёхпростое число, при фиксированном p и q, удовлетворяющих следующим условиям:
Итоговая оценка для такой ситуации :
Второй подход к оценке эффективности основан на свойствах функции определённой следующим образом:
Теперь укажем теорему, на которой построена другая оценка:
Теорема 2. Пусть произвольное число, представимое в виде
, где
– простое. Тогда для того, чтобы
было строго псевдопростым по базе
необходима делимость
на
.
Используя теорему 2 и оценки количества делителей, мы получаем верхнюю оценку для ошибки теста Миллера-Рабина, но только для полупростых чисел:
Однако реальные значения не достигают верхней оценки. Значит эту оценку можно улучшить.
Третий подход к оценке эффективности – вычисление последовательности чисел – наименьшее строго псевдопростое число для
первых простых чисел. Ж. Женхианг смог получить кандидатов для значений первых 19 элементов последовательности. До настоящего времени смогли доказать эту гипотезу только для первых 13 элементов последовательности.
Рассматривая уже полученные результаты, можно сделать вывод о том, что последовательность очень быстро возрастает. Однако эффективный алгоритм поиска очередного алгоритма пока не найден, поэтому поиск следующего элемента последовательности затруднителен.
Наиболее оптимальный переборный алгоритм , который использовался для поиска последних известных элементов последовательности основан на Теореме 2 и следующих утверждениях:
Утверждение 1. Если для произвольных простых чисел и
выполняется
и
, то
.
Утверждение 2. Если для произвольных простых чисел и
выполняется
и
, то
.
Сам алгоритм состоит из двух методов, каждый из которых выполняет перебор возможных кандидатов по своим критериям.
Первый метод использует НОД для получения всех кандидатов. На вход метод получает число . В ходе алгоритма вычисляются все
для всех оснований
. Затем вычисляется НОД полученных значений.
получаются путём перебора всех делителей НОД. Второй метод используя утверждения 1 и 2 перебирает все возможные остатки по достаточно большому модулю. После чего получаются перебором всех простых чисел с заданным остатком по модулю.
Поскольку первый метод эффективней на маленьких числах, а второй метод на больших, то первый метод применяется для всех , где
– верхняя граница отрезка на котором производится поиск, а второй метод для остальных
. Значение границы для методов было получено теоретическим путём для наиболее оптимального раздела.
Также для быстрого перебора используется хэш-таблица в которой хранятся все простые числа
и значения
для всех оснований
. В качестве ключа используется хеш-значения от значений
. Поскольку все значения из хэш-таблицы используются для формирования составных чисел, состоящих не менее чем из 3 делителей, то и хранить достаточно лишь все простые числа
.
Таким образом итоговый алгоритм получается следующий:
Algorithm 1.
– хэш-таблица,
– граница для перебора,
– набор оснований.
Перебираем все простые числа от
до
:
Вычисляем все .
Получаем список всех простых чисел из с совпадающими значениями
.
Формируем все возможные значения :
Если , то перебираем всех кандидатов на строго псевдопростоту с помощью первого метода.
Иначе, с помощью второго.
Если , то добавляем в
вместе со всеми значениями
.
3. Основные результаты
Поскольку последовательность чисел растёт достаточно быстро, то рассматриваемые границы для поиска также будут сильно увеличиваться. Это приведёт не только к замедлению времени работы, но и увеличению объёма используемой памяти. Например,
, следовательно, в хэш-таблице будет храниться порядка
элементов, что крайне много для хранения на компьютере. Поэтому необходимо модифицировать алгоритм 1, чтобы он затрагивал меньше памяти.
Для начала рассмотрим распределение простых чисел на отрезке по значению . Для ускорения вычисления мы введём следующую функцию:
Определение 1. Пусть и
– произвольные числа,
– простое, a
определяется следующим образом:
Тогда функция , определяется следующим образом:
Эффективный поиск значения этой функции выполняется следующим алгоритмом:
Алгоритм 2.
– простое,
– натуральное числа,
Посчитаем
Посчитаем
Пока не станет равным 1 выполняем:
Значение устанавливается результатом функции
Вычислительная сложность данного алгоритма .
Для использования данного алгоритма докажем следующую теорему:
Теорема 3. Пусть произвольное число, тогда выполняется следующее соотношение:
Доказательство. Пусть . Тогда возможно 2 варианта:
1. .
→
найден неверно.
2. .
– целое
→
найден неверно.
Значит остаётся единственный вариант в (21).
Таким образом, заменив вычисление на
, мы получим тот же результат, но за меньшее время.
4. Обсуждение
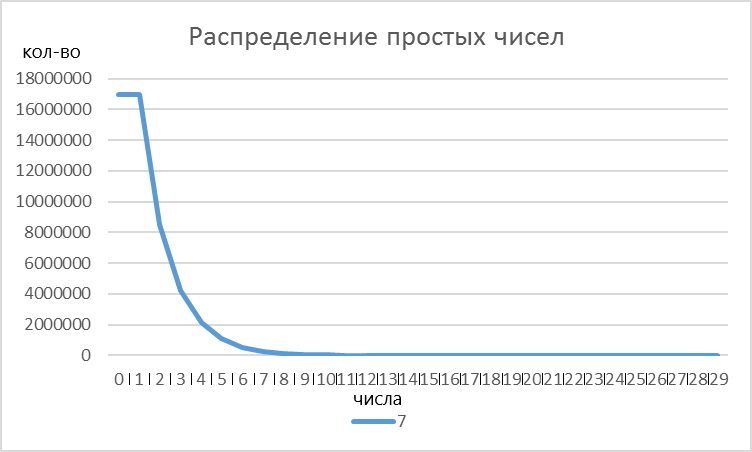
Рисунок 1 - Распределение простых чисел по значениям для основания 7
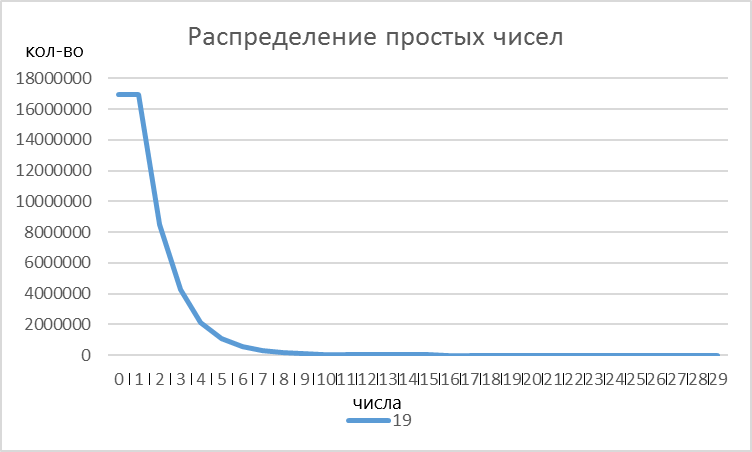
Рисунок 2 - Распределение простых чисел по значениям для основания 19
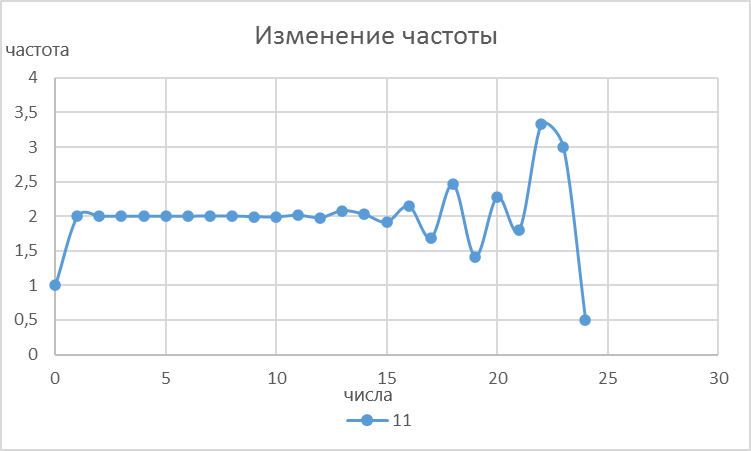
Рисунок 3 - Отношение количеств простых чисел на соседних значениях
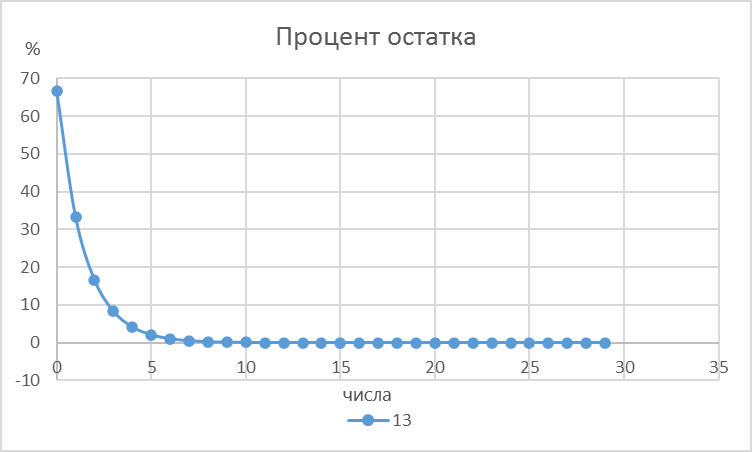
Рисунок 4 - Процент оставшегося количества чисел
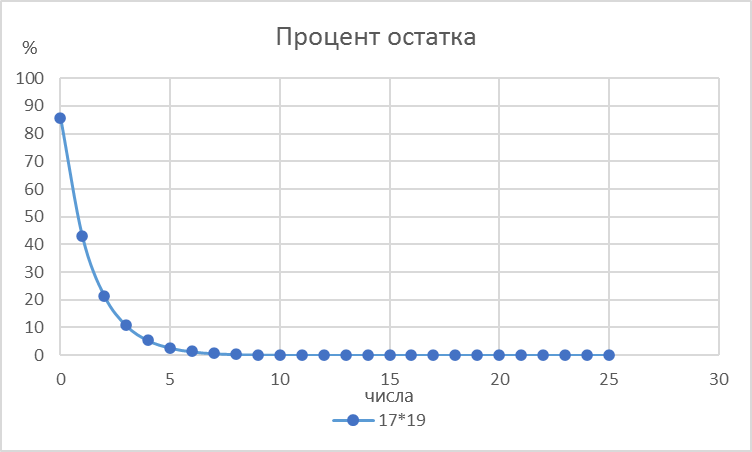
Рисунок 5 - Процент оставшегося количества чисел
1 этап – перебрать все простые числа со значением всех меньше заданного порогового значения
с помощью алгоритма 2. При этом само значение
перебирать из некоторого фиксированного набора
.
2 этап – перебрать все простые числа со значением хотя бы одного не меньше
с помощью другого, возможно менее эффективного для большого количества чисел, алгоритма.
Пример такого алгоритма:
Алгоритм 3.
– список простых чисел,
– список контейнеров для простых чисел
Перебираем все основания :
Очищаем все контейнеры в
Перебираем все числа из
:
Вычисляем
Переносим из
в
Переносим последовательно все простые числа из контейнеров в
Вычислительная сложность данного алгоритма
5. Заключение
В рамках данной работы были представлены текущие результаты по оценке эффективности теста Миллера-Рабина. Было продемонстрировано три разных подхода, сделаны выводы о возможном направлении для каждого подхода. Для модификации был выбран третий подход – поиск последовательности чисел – наименьшее строго псевдопростое число для
первых простых чисел.
Было обнаружено «бутылочное горлышко» для исходного алгоритма – им оказался расход памяти на хэш-таблицу. Поэтому дальнейшие исследования направлены на оптимизацию расхода памяти.
Были сделаны выводы о распределении простых чисел по значениям и рассмотрен вариант использования полученных данных для модификации алгоритма.
Была представлена новая схема алгоритма со сравнимым временем работы, но уменьшенным расходом памяти.
