Наши журналы
Опубликовать статью Вход и регистрация
Расширенный поиск
Разделы статьи

СРАВНИТЕЛЬНЫЙ АНАЛИЗ МЕТОДОВ ЧИСЛЕННОГО РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ

Научная статья
Богданов А.Е.
Торшина О.А.
DOI:
https://doi.org/10.23670/IRJ.2019.82.4.006
Выпуск: № 4 (82), 2019
Опубликована:
2019/04/25
PDF

СРАВНИТЕЛЬНЫЙ АНАЛИЗ МЕТОДОВ ЧИСЛЕННОГО РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ

Научная статья

Богданов А.Е.1, Торшина О.А.2, *

2 ORCID: 0000-0003-3999-0622,

1, 2 Федеральное государственное бюджетное образовательное учреждение высшего образования Магнитогорский государственный технический университет им. Г.И. Носова, Магнитогорск, Россия

* Корреспондирующий автор (olganica[at]mail.ru)

Аннотация

К нелинейным системам уравнений и необходимости их решения приводит рассмотрение многих прикладных задач, к которым относятся краевые задачи для обыкновенных дифференциальных уравнений и для уравнений с частными производными (разрешаемые методом конечных разностей), задачи оптимизации, задачи минимизации функций многих переменных, применение неявных методов интегрирования обыкновенных дифференциальных уравнений и т.д. Численное решение систем нелинейных уравнений в общем случае задача более сложная, нежели решение систем линейных уравнений, поскольку не существует методов, гарантирующих успех решения любой такой задачи. Выявление оптимального метода и его дальнейший выбор позволяет увеличить шансы на успешное решение систем нелинейных уравнений. В связи с актуальностью вышеизложенного в данной статье представлены алгоритмы методов численного решения систем нелинейных уравнений, согласно которым произведен поиск корней типовой для прикладных задач системы. По полученным результатам проведен сравнительный анализ с целью выявления оптимального метода. Оптимальным считается тот метод, которым найдены значения всех корней системы с требуемой точностью за наименьшее число итераций.

Ключевые слова: краевые задачи, системы нелинейных уравнений, численные методы, дифференциальные уравнения.

COMPARATIVE ANALYSIS OF COMPUTATIONAL METHODS OF SYSTEM OF NONLINEAR EQUATIONS

Research article

Bogdanov A.E.1, Torshina O.A.2, *

2 ORCID: 0000-0003-3999-0622,

1,2 Federal State Budgetary Educational Institution of Higher Education, Nosov Magnitogorsk State Technical University, Russia, Magnitogorsk

*Corresponding author (olganica[at]mail.ru)

Abstract

The consideration of numerous applied problems leads to systems of nonlinear equations, they include boundary problems for ordinary differential equations and partial differential equations (solved by the finite difference method), optimization problems, problems of minimization of functions of many variables, the use of implicit methods for integrating ordinary differential equations, etc. Numerical solution of systems of nonlinear equations in the general case is a more complicated problem than the solution of systems of linear equations, since there are no methods that guarantee the success of solving any problem of this kind. Identifying the optimal method and its further selection allows you to increase the chances of successfully solving systems of nonlinear equations. In connection with the relevance of the above-mentioned, this article presents the algorithms for methods for the numerical solution of systems of nonlinear equations, according to which the root of a typical system for applied problems was searched. According to the obtained results, a comparative analysis was conducted in order to identify the optimal method. The optimal method is the one that found the values of all the roots of the system with the required accuracy in the least number of iterations.

Keywords: boundary value problems, systems of nonlinear equations, numerical methods, differential equations.

Введение В общем случае системы n нелинейных уравнений с n неизвестными  принято записывать следующим образом (1).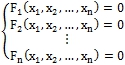 08-05-2019 16-03-27   (1)

Где 08-05-2019 16-07-24  – функции независимых переменных.

Решением системы (1) является вектор (векторы) 08-05-2019 16-07-35, при подстановке которого все уравнения системы обращаются в тождества (2).

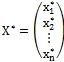08-05-2019 16-07-50   (2)

Количество решений (единственное, конечное, бесконечное) зависит от рассматриваемого частного случая.

Решение системы (1) можно разбить на три этапа: графическое разделение корней, выбор оптимальных начальных приближений, преобразование системы к требуемому методами виду с последующим поиском численных решений согласно алгоритмам.

Графическое разделение корней сводится к построению графика для системы (1) в любом математическом пакете, обладающем необходимыми графическими средствами (Maple, MathCad). На основании построенного графика можно сделать вывод о количестве решений системы и выбрать оптимальные нулевые приближения для поиска каждого корня рассматриваемыми численными методами.

Оптимальными нулевыми приближениями будут такие значения, которые при визуальном анализе графика расположены к корню наиболее близко. От правильности выбора нулевого приближения зависит успех сходимости итерационных процессов рассматриваемых методов.

В рамках статьи рассмотрены следующие итерационные процессы поиска корней: «метод простых итераций», «метод Ньютона», «метод секущих».

Условия сходимости итерационных процессов можно оценивать различными способами, в числе которых «принцип сжимающих отображений», представленный следующей теоремой: последовательность 08-05-2019 16-13-34,  элементов n-мерного евклидова пространства, порожденная итерационным процессом 08-05-2019 16-13-48 сходится к решению X системы нелинейных алгебраических уравнений 08-05-2019 16-14-07, если отображение 08-05-2019 16-14-17 является сжимающим; при этом выполнено 08-05-2019 16-14-27.

Полученные результаты могут быть использованы при решении задач рассмотренных в работах [4]-[10].

Постановка и решение задачи

Рассмотрим систему нелинейных уравнений:

08-05-2019 16-17-51   (3)

Для численного решения заданной системы (3) осуществим описанные во введении для общего случая этапы и выполним сравнительный анализ результатов, полученных рассматриваемыми методами.

Этап 1. Графическое разделение корней [1].

Для построения графика система (3) преобразована к виду (4):

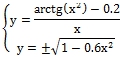08-05-2019 16-18-04    (4)

Для преобразованной системы (4) построен график в математическом пакете Maple (рис. 1).

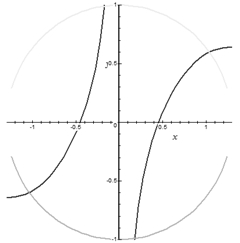
08-05-2019 16-19-49

Рис. 1 – График системы (4) построенный в пакете Maple

 

После визуального анализа рисунка 1 можно сделать следующие выводы:

  1. Система (3) имеет 4 решения.
  2. Корни в рассматриваемой системе – точки пересечения эллипса с гиперболой. На графике видно, что значения корней в 1 и 3 четвертях будут противоположными. Тоже самое можно сказать про значения во 2 и 4 четвертях. Это значит, что поиск корня можно осуществлять либо только в 1 и 4, либо во 2 и 3 четвертях. Далее будем искать решение в 1 и 4 четвертях.

Этап 2. Выбор оптимальных начальных приближений [1].

Графическое разделение корней (этап 1) позволяет сделать оценки первых приближений. Оптимальные начальные приближения: 08-05-2019 16-21-04.

Этап 3. Преобразование системы к требуемому методами виду с последующим поиском численных решений согласно алгоритмам.

Алгоритм метода простых итераций [2].

  1. Задать начальное приближение 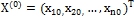08-05-2019 16-22-35 и малое положительное число ε (точность). Положить 08-05-2019 16-23-16.
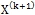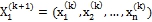  2. Вычислить 08-05-2019 16-23-27 по формуле: 08-05-2019 16-24-10.
  3. Если 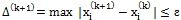08-05-2019 16-25-24 процесс завершен и 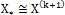08-05-2019 16-25-37. Если 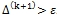08-05-2019 16-25-45, то положить 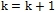08-05-2019 16-25-56 и перейти к пункту 2.

Если данный итерационный процесс сходится, то он сходится к решению системы уравнений.

Для сходимости итерационного процесса необходимо, чтобы норма производной вектор-функции 08-05-2019 16-48-42  была меньше некоторого положительного числа 08-05-2019 16-48-52 в некоторой окрестности Ψ области решения системы, из которой не выходят приближенные значения 08-05-2019 16-49-24 при итерации 08-05-2019 16-49-42.

Для применения метода требуется привести систему уравнений (3) к равносильному виду:

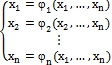08-05-2019 16-52-43   (5)

где 08-05-2019 17-06-42  функции 08-05-2019 17-06-51 определены и непрерывны в окрестности изолированного решения 08-05-2019 17-08-20  системы (5).

Система может быть преобразована к виду (5) различными способами. Способ записи уравнений играет особую роль, так как это влияет на выполнение условия сходимости при численном решении. Чтобы ответить на вопрос, выполняется ли условие сходимости в рассматриваемом примере:

  1. составлены все возможные выражения из системы (3), пригодные для приведения к виду системы (5).
  2. вычислены нормы частных производных от правых частей этих выражений в нулевом приближении.
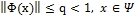  3. просуммированы суммы найденных норм для каждой вектор-функции и выбраны те, которые соответствуют условию 08-05-2019 16-49-42.

Нормы производных для системы (3) представлены в таблицах 1-4.

 

Таблица 1 – Нормы производных для 08-05-2019 17-10-10 в нулевом приближении (0.2;-0.9)

08-05-2019 17-10-29

Условие сходимости итерационного процесса выполняется только в первом и третьем случае. В других случаях нормы производных больше 1, итерационный процесс будет расходящимся.

 

Таблица 2 – Нормы производных для 08-05-2019 17-12-53  в нулевом приближении (0.2;-0.9)

08-05-2019 17-13-04

Условие сходимости итерационного процесса выполняется только во втором случае.  

Таблица 3 – Нормы производных для 08-05-2019 17-10-10 в нулевом приближении (1;0.6)

08-05-2019 17-16-55

Во всех случаях нормы производных больше единицы, итерационный процесс будет расходящимся.  

Таблица 4 – Нормы производных для 08-05-2019 17-12-53 в нулевом приближении (1;0.6)

08-05-2019 17-20-41

08-05-2019 17-22-16

Алгоритм будет следующим:

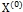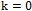  1. Задать начальное приближение 08-05-2019 17-22-45 и малое положительное числоε (точность). Положить 08-05-2019 17-22-59.
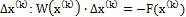  2. Решить систему линейных алгебраических уравнений относительно поправки 08-05-2019 17-23-14.
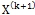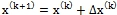  3. Вычислить 08-05-2019 17-23-26 по формуле: 08-05-2019 17-23-34.
  4. Если 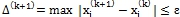08-05-2019 17-23-48 процесс завершен и 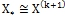08-05-2019 17-23-59 . Если 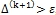08-05-2019 17-24-08, то положить 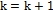08-05-2019 17-24-16  и перейти к пункту 2.

Алгоритм метода секущих [4].

  1. Задать начальное приближение 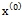08-05-2019 17-32-13  и малое положительное число ε (точность).
  2. Положить 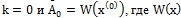08-05-2019 17-32-03 – матрица Якоби.
  3. Решить систему линейных алгебраических уравнений 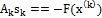08-05-2019 17-32-21 относительно 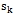08-05-2019 17-32-27 – поправки к текущему приближению.
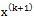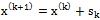  4. Вычислить 08-05-2019 17-32-51 по формуле: 08-05-2019 17-32-57.
  5. Если 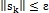08-05-2019 17-33-07, процесс завершить и положить 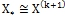08-05-2019 17-23-59. Если 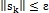08-05-2019 17-33-07, то вычислить: 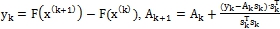08-05-2019 17-33-35 положить 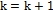08-05-2019 17-24-16 и перейти к пункту 3.

Заключение

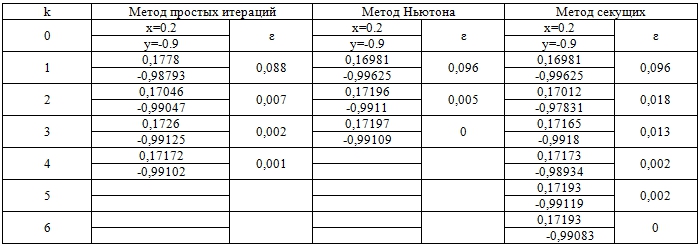
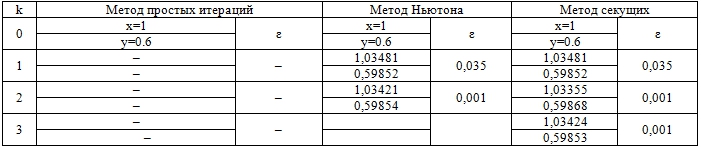
Результаты численного решения системы нелинейных уравнений (3) по рассмотренным выше алгоритмам приведены в таблицах 5-6.

 

Таблица 5 – Расчетная таблица для нулевого приближения (0.2;-0.9)

08-05-2019 17-40-21

 

Из таблицы 5 видно, что все методы для начального приближения (0.2;-0.9) дали результаты, близкие к точному решению. Однако количество итераций методов различно.

 

Таблица 6 – Расчетная таблица для нулевого приближения (1;0.6)

08-05-2019 17-45-11

Результаты в таблице 6 для начального приближения (1;0.6) указывают на то, что метод простых итераций расходится (в соответствии с условием сходимости данного метода). Остальные методы сходятся, показав различное число итераций.

Согласно результатам сравнительного анализа, в качестве оптимального метода может быть выбран «Метод Ньютона», так как он сошелся для всех корней рассматриваемой системы нелинейных уравнений с требуемой точностью за наименьшее число итераций.

Конфликт интересов Не указан. Conflict of Interest None declared.

Список литературы / References

  1. Бахвалов Н.С Численные методы. / Н.С. Бахвалов, Н.П. Жидков,  Г.М. Кобельков - Москва. Лаборатория Базовых Знаний. 2002. - С. 324-330.
  2. Ортега Д. Итерационные методы решения систем уравнений со многими неизвестными / Д. Ортега, В. Рейнболдт - Москва. Мир. 1975. - С. 180-232.
  3. Нестеров Ю.Е. Эффективные методы в нелинейном программировании / Ю.Е. Нестеров - Москва, Радио и связь. - 1989. - 304 с.
  4. Дубровский В.В. Дискретность спектра задачи Неймана / В.В. Дубровский, О.А. Торшина // Вестник Магнитогорского государственного университета. - 2004. - №5. - С. 130-131.
  5. Дубровский В.В. Об одной лемме спектральной теории оператора Штурма - Лиувилля / В.В. Дубровский, О.А. Торшина //Проблемы науки и образования в современной высшей школеТезисы докладов XXXVIII внутривузовской научной конференции преподавателей МаГУ. - 2000. - С. 42-43.
  6. Кадченко С.И. Вычисление собственных чисел эллиптических дифференциальных операторов с помощью теории регуляризованных рядов / С.И. Кадченко, О.А. Торшина // Вестник Южно-Уральского государственного университета. Серия: Математика. Механика. Физика. - 2016. - Т. 8. -№ 2. - С. 36-43.
  7. Торшина О.А. Существенный спектр задачи Неймана для оператора Лапласа / О.А. Торшина //Современные проблемы науки и образования: материалы L внутривузовской научной конференции преподавателей МаГУ. – Магнитогорск: Издательство Магнитогорский государственный университет, 2012. - С. 271.
  8. Торшина О.А. Формула асимптотики собственных чисел оператора Лапласа – Бельтрами с потенциалом на проективной плоскости / О.А. Торшина //Современные методы теории функций и смежные проблемы.Материалы конференции. - 2003. - С. 258-259.
  9. Торшина О.А. Формула регуляризованного следа дифференциального оператора со сложным вхождением спектрального параметра / О.А. Торшина // Вестник Тамбовского университета. Серия: Естественные и технические науки. - 2003. - Т. 8.- №3. - С. 467-468.
  10. Торшина О.А. К вопросу сложения четных сферических гармоник / О.А. Торшина // Вестник Магнитогорского государственного университета. - 2004.- №6. - С. 73-77.

Список литературы на английском языке / References in English

  1. Bakhvalov N.S. Chislennyye metody [Numerical Methods] / N.S. Bakhvalov, N.P. Zhidkov, G.M. Kobelkov – Moscow. Laboratory of Basic Knowledge. 2002. – P. 324-330. [In Russian]
  2. Ortega D. Iteratsionnyye metody resheniya sistem uravneniy so mnogimi neizvestnymi [Iterative Methods for Solving Systems of Equations with Many Unknowns] / D. Ortega, V. Reinboldt – Moscow. World. 1975. – P. 180-232. [In Russian]
  3. Nesterov Yu.E. Effektivnyye metody v nelineynom programmirovanii [Effective Methods in Nonlinear Programming] / Yu.E. Nesterov – Moscow, Radio and communications. – 1989. – 304 p. [In Russian]
  4. Dubrovsky V.V. Diskretnost' spektra zadachi Neymana [Discreteness of the Spectrum of Neumann Problem] / V.V. Dubrovsky, O.A. Torshina // Vestnik Magnitogorskogo gosudarstvennogo universiteta [Bulletin of Magnitogorsk State University]. – 2004. – No. 5. – P. 130-131. [In Russian]
  5. Dubrovsky V.V. Ob odnoy lemme spektral'noy teorii operatora Shturma - Liuvillya [On One Lemma of Spectral Theory of Sturm-Liouville Operator] / V.V. Dubrovsky, O.A. Torshina // Problemy nauki i obrazovaniya v sovremennoy vysshey shkole Tezisy dokladov XXXVIII vnutrivuzovskoy nauchnoy konferentsii prepodavateley MaGU [Problems of Science and Education in the Modern Higher School Abstracts of the XXXVIII intra-university scientific conference of teachers of the Moscow State University]. – 2000. – P. 42-43. [In Russian]
  6. Kadchenko S.I. Vychisleniye sobstvennykh chisel ellipticheskikh differentsial'nykh operatorov s pomoshch'yu teorii regulyarizovannykh ryadov [Calculation of Eigenvalues of Elliptic Differential Operators Using Theory of Regularized Series] / S.I. Kadchenko, O.A. Torshina // Vestnik Yuzhno-Ural'skogo gosudarstvennogo universiteta. Seriya: Matematika. Mekhanika. Fizika [Bulletin of the South Ural State University. Series: Mathematics. Mechanics. Physics]. – 2016. – V. 8. – No. 2. – P. 36-43. [In Russian]
  7. Torshina O.A. Sushchestvennyy spektr zadachi Neymana dlya operatora Laplasa / O.A. Torshina [Essential Spectrum of Neumann Problem for Laplace Operator] / O.A. Torshina // Sovremennyye problemy nauki i obrazovaniya: materialy L vnutrivuzovskoy nauchnoy konferentsii prepodavateley MaGU. – Magnitogorsk: Izdatel'stvo Magnitogorskiy gosudarstvennyy universitet [Modern Problems of Science and Education: Proceedings of the L intrauniversity scientific conference of teachers of the Moscow State University. – Magnitogorsk: Magnitogorsk State University Publishing House], 2012. – P. 271. [In Russian]
  8. Torshina O.A. Formula asimptotiki sobstvennykh chisel operatora Laplasa – Bel'trami s potentsialom na proyektivnoy ploskosti [Formula for Asymptotics of Eigenvalues of Laplace – Beltrami operator with Potential on Projective Plane] / O.A. Torshina // Sovremennyye metody teorii funktsiy i smezhnyye problemy. Materialy konferentsii [Modern methods of the theory of functions and related problems. Conference proceedings. – 2003. – P. 258-259. [In Russian]
  9. Torshina O.A. Formula regulyarizovannogo sleda differentsial'nogo operatora so slozhnym vkhozhdeniyem spektral'nogo parametra [Formula for Regularized Trace of Differential Operator with Complex Occurrence of Spectral Parameter] / O.A. Torshina // Vestnik Tambovskogo universiteta. Seriya: Yestestvennyye i tekhnicheskiye nauki [Bulletin of the Tambov University. Series: Natural and Technical Sciences]. – 2003. – V. 8. – No. 3. – P. 467-468. [In Russian]
  10. Torshina O.A. K voprosu slozheniya chetnykh sfericheskikh garmonik [On Question of Addition of Even Spherical Harmonics] / O.A. Torshina // Vestnik Magnitogorskogo gosudarstvennogo universiteta [Bulletin of Magnitogorsk State University]. – 2004. – No. 6. – P. 73-77. [In Russian]