МАГНИТОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ В ТРЕХСЛОЙНОЙ СТРУКТУРЕ НИКЕЛЬ – КВАРЦ – НИКЕЛЬ

МАГНИТОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ В ТРЕХСЛОЙНОЙ СТРУКТУРЕ НИКЕЛЬ – КВАРЦ – НИКЕЛЬ

Научная статья

Маничева И.Н.¹, Филиппов Д.А.^2, *, Лалетин В.М.³,

¹ ORCID: 0000-0002-5282-2263;

² ORCID: 0000-0002-4359-7770;

³ ORCID: 0000-0002-3531-0629;

^{1, 2} Новгородский государственный университет имени Ярослава Мудрого, Великий Новгород, Россия;

³ Институт технической акустики, Витебск, Беларусь

* Корреспондирующий автор (Dmitry.Filippov[at]novsu.ru)

Аннотация

Представлены результаты теоретических и экспериментальных исследований магнитоэлектрического эффекта в композитных трехслойных структурах никель – кварц - никель. Образцы в форме пластинки были изготовлены методом склеивания. Установлено, что в области электромеханического резонанса величина магнитоэлектрического коэффициента по напряжению составляла α =84,7 V / сm Oe, при добротности Q = 93. Применение кварца в качестве пьезоэлектрического слоя позволяет получать величину магнитоэлектрического эффекта в композиционных структурах, сравнимую с лучшими образцами на основе цирконата-титаната свинца.

Ключевые слова: магнитоэлектрический эффект, магнитострикция, пьезоэлектричество, кварц, электромеханический резонанс.

MAGNETOELECTRIC EFFECT IN THREE LAYER NICKEL – QUARTZ – NICKEL STRUCTURE

Research article

Manicheva I.N.¹, Filippov D.A.^2, *, Laletin V.M.³

¹ ORCID: 0000-0002-5282-2263;

² ORCID: 0000-0002-4359-7770;

³ ORCID: 0000-0002-3531-0629;

^{1, 2} Yaroslav-the-Wise Novgorod State University; Veliky Novgorod, Russia;

³ Institute of Technical Acoustics; Vitebsk, Belarus

* Corresponding author (Dmitry.Filippov[at]novsu.ru)

Abstract

The results of theoretical and experimental studies of the magnetoelectric effect in composite three – layer structures of nickel - quartz-nickel are presented. Samples in the form of plates were made by gluing. At the electromechanical resonance region the value of the magnetoelectric voltage coefficient α = 84.7 V / cm Oe, with Q = 93 was observed. Using the quartz as a piezoelectric layer allows to obtain the magnitude of the magnetoelectric effect in composite structures, comparable to the best samples based on lead zirconate-titanate.

Keywords: magnetoelectric effect, magnetostriction, piezoelectricity quartz, electromechanical resonance.

Введение

Интенсивное исследование перекрестных эффектов в композитных структурах, обусловленных механическим взаимодействием фаз, входящих в состав композита, привело к созданию нового направления в физике конденсированного состояния – стрейнтроники, в основе которого лежат методы деформационной инженерии [1, C. 1288]. Магнитоэлектрический (МЭ) эффект относится к одному из таких перекрестных эффектов и связывает между собой магнитные и электрические характеристики вещества. Он представляет особый интерес ввиду его перспективного использования при создании приборов твердотельной электроники, таких как гираторы [2, P. 015004], управляемые электрическим полем катушки индуктивности [3, P. 113502], датчики магнитного поля, чувствительность которых превосходит чувствительность датчиков Холла [4, P. 244]. МЭ эффект в композитах возникает в результате механического взаимодействия магнитострикционной (МС) и пьезоэлектрической (ПЭ) фаз. Механические деформации, вызываемые в МС фазе переменным магнитным полем передаются через границу раздела в ПЭ фазу, приводя к изменению поляризации и возникновению электрического напряжения. МЭ композиты делят на объемные и слоистые. Объемные композитные структуры, полученные по керамической технологии методом спекания смесей порошков МС и ПЭ компонентов, достаточно просты в изготовлении, обладают хорошими механическими свойствами [5, С. 47]. Слоистые композиты, состоящие из чередующихся слоев МС и ПЭ фаз, имеют ряд преимуществ по сравнению с объемными МЭ композитами: легко поляризуются, обладают малыми токами утечки [6, С. 214408]. В качестве МС фазы можно применять материалы с большим коэффициентом магнитострикции (никель, пермендюр аморфные и редкоземельные сплавы) [7, С. 2076], [8, С.123918], [9, С. 497]. В качестве пьезоэлектрика используют материалы, обладающие высоким значением пьезомодуля (цирконат-титанат свинца – PZT, кристаллы лангатата, ниобата лития и т.д.) [10, С. 224]. Выбор никеля в качестве материала для МС фазы обусловлен максимальной величиной коэффициента магнитострикции при малых значениях напряженности поля подмагничивания. Величина МЭ эффекта прямо пропорциональна величине пьезомодуля и обратно пропорциональна значению диэлектрической проницаемости пьезоэлектрика [11, С. 2168]. Несмотря на небольшое значение пьезомодуля кварца () и значение диэлектрической проницаемости (), его использование в качестве подложек для изготовления МЭ структур может показывать большие значения МЭ эффекта. Кроме того, кварц является монокристаллом с более стабильными свойствами, в отличие от ЦТС, исключает операцию предварительной поляризации, что значительно упрощает процесс изготовления слоистых МЭ структур.

Исследованная трехслойная структура схематически изображена на рис. 1.

Рис.1 – Схематичное изображение структуры 1 – МС слой, 2– слой клея, 3 – ПЭ слой

В качестве пьезоэлектрика использован образец, вырезанный из пластины кварца (X-срез) в форме параллелепипеда с размерами 20 × 4.5 × 0.5 mm, длинная сторона которого совпадает с направлением <011>. Он расположен между двумя пластинами никеля толщиной по 0,25 mm, которые присоединены к кварцевой пластине при помощи эпоксидного клея. В структуре возникают планарные и толщинные колебания. Для планарных колебаний характерные резонансные частоты определяются длиной и шириной образца, для толщинных колебаний – толщиной структуры. Если считать образец длинным и узким, т.е. , то частота резонанса для колебаний, распространяющихся по длине образца, будет много меньше частоты колебаний, распространяющихся по ширине и толщине образца и в первом приближении их можно рассматривать как независимые. При распространении колебаний по длине образца имеют место планарные колебания, которые связаны с однородной деформацией типа растяжение – сжатие, и изгибные колебания, связанные с деформациями типа изгиба. Возбуждение колебаний в структуре происходит путем их возбуждения в МС фазе и передачи посредством касательных напряжений в ПЭ слой. Поскольку рассматриваемая структура является симметричной относительно ПЭ подсистемы, то возбуждение колебаний в пьезоэлектрике будет осуществляться одновременно с обеих сторон. В симметричной структуре изгибные колебания возбуждаться не будут и можно рассматривать только планарные колебания. Поэтому исследуемый многослойный образец, можно представить в виде структуры пьезоэлектрик – соединительный слой – магнетик (рис. 2) с учетом только планарных колебаний.

 

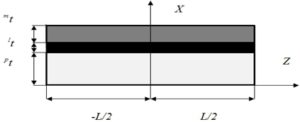
Рис. 2 – Схематичное изображение модели многослойной структуры

 

Для нахождения МЭ коэффициента по напряжению сэндвич структуры воспользуемся методом, разработанным ранее в работах [12, С. 1730], [13, С. 1088]. Поскольку толщина ПЭ, МС и соединительного слоя много меньше длины образца, поэтому в первом приближении можно считать, что смещения слоев одинаковы. В этом приближении уравнение движения для z- проекции вектора смещения среды имеют вид:

   (1)

где  – среднее значение плотности структуры, и   – среднее значение тензора напряжений структуры, - толщина магнетика, пьезоэлектрика и клеевого слоев соответственно. Уравнения для тензора деформаций ПЭ фазы , МС фазы, и x-проекции вектора электрической индукции  в этом приближении имеют вид:

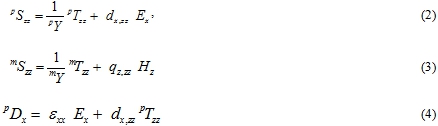
где  – компоненты тензора напряжений и модули Юнга ПЭ и МС фаз;  – ПЭ и пьезомагнитный коэффициенты,  – тензор диэлектрической проницаемости.

Компоненты ПЭ тензора в системе координат XYZ связаны с компонентами тензора в кристаллографической системе координат соотношением в виде:

   (5)

где  – матрица косинусов между осью Z и осями 2 и 3 (между направлением <011> и направлениями <010> и <001>).

Решение уравнения (1) для вектора смещения среды представим в виде плоских волн, распространяющихся вдоль длины образца:

   (6)

где  и - постоянные интегрирования. Подставляя выражение (6) в уравнение (1), получим выражение для дисперсионного соотношения:

   (7)

Используя условия механического равновесия на торцах образца, в точках  получаем граничные условия:    (8) Для постоянных интегрирования  и получим:    (9)

где введен параметр . Выражая компоненту тензора напряжений через компоненты тензора деформаций и подставляя  выражение в уравнение для нормальной компоненты вектора электрической индукции, получим:

  (10)

Воспользуемся условием разомкнутой цепи, а именно:    (11)

Подставляя выражение (10) в уравнение (11) и проинтегрировав, получим выражение для определения напряженности электрического поля:

  (12) где введено обозначение    (13)

где  – квадрат коэффициента электромеханической связи.

Используя определение МЭ коэффициента, как  получим:

   (14)

Когда параметр , имеет место резонансное увеличение МЭ

коэффициента по напряжению. Поскольку , то резонансное увеличение МЭ эффекта происходит при значении , что соответствует условию, когда на длинной стороне образца укладывается половина длины волны. Используя дисперсионное соотношение (7) для резонансной частоты получим:

   (15)

Выражение (15) показывает, что резонансная частота зависит от модуля Юнга, толщины каждого слоя и длины образца.

Для определения частотной и полевой зависимости МЭ эффекта использовался метод регистрации переменного электрического напряжения на образце при помещении его в постоянное подмагничивающее поле напряженностью H_bias и переменное магнитное поле H, направленные вдоль длинной стороны образца. На рис. 3 приведена частотная зависимость МЭ эффекта в области резонанса.

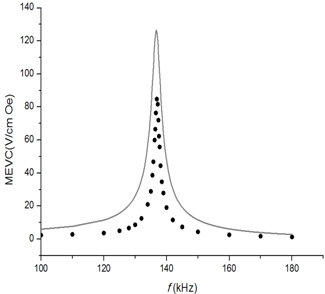
Рис. 3 – Частотная зависимость МЭ коэффициента по напряжению (MEVC) в области электромеханического резонанса

 

Как видно из графика, в полном соответствие с теорией, на частоте 138 kHz наблюдается пиковое увеличение МЭ коэффициента по напряжению, обусловленное наличием электромеханического резонанса. Значения резонансной частоты, рассчитанное теоретически и полученное экспериментально, хорошо согласуются между собой. Небольшое отличие наблюдается в величине значения МЭ коэффициента по напряжению. Это отличие обусловлено тем, что амплитудное значение МЭ коэффициента по напряжению прямо пропорционально произведению пьезоэлектрического и пьезомагнитного коэффициентов. Если величина пьезоэлектрического коэффициента определяется достаточно точно, то величина пьезомагнитного коэффициента зависит от величины поля подмагничивания и определяется путем дифференцирования кривой магнитострикции, в результате чего возникает погрешность в определении его величины. Кроме того, амплитудное значение МЭ коэффициента по напряжению при резонансе очень сильно зависит от параметра затухания, который также определяется недостаточно точно. Совокупность этих факторов и приводит к различию между теорией и экспериментом.

Заключение

Таким образом, слоистая композиционная структура, где в качестве ПЭ фазы использован кварц, имеет добротность Q = 93, что превышает добротность клеевой структуры Ni – ЦТС – Ni более чем в 1,5 раза [14, С. 103]. Значение МЭ коэффициента по напряжению в области электромеханического резонанса структуры на основе кварца также превосходит величину для структуры на основе ЦТС в 15 раз, что позволяет слоистым композиционным МЭ структурам Ni – Q – Ni найти широкое применение в стрейнтронике и спинтронике [15, C. 344].

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Бухараев А.А. Стрейнтроника – новое направление микро- и наноэлектроники и науки о материалах / А.А. Бухараев, А.К. Звездин, А.П.Пятаков, Ю.К. Фетисов // УФН. – 2018. – Т. 188.- №12. – С. 1288 - 1330.
2. Zhang Highly efficient power conversion in magnetoelectric gyrators with high quality factor / J. Zhang, W. Zhu, D.A. Filippov, W.He, D. Chen, K. Li, S. Geng, Q. Zhang, L. Jiang, L. Cao, R. Timilsina, and G. Srinivasan // Rev. Sci. Instrum. – 2019. – Vol. 90. – P. 015004.
3. Zhang Bidirectional tunable ferrite-piezoelectric trilayer magnetoelectric inductors / J. Zhang, D. Chen, D. A. Filippov, K. Li, Q. Zhang, L. Jiang, W. Zhu, L. Cao, G. Srinivasan // Appl. Phys. Lett. – 2018. – Vol. 113. – P. 113502.
4. Burdin D.A. High-sensitivity DC field magnetometer using nonlinear resonance magnetoelectric effect / D.A. Burdin, D.V. Chashin, N.A. Ekonomov, Y.K. Fetisov, A.A. Stashkevich // Journal of Magnetism and Magnetic Materials. - 2016. - Vol. 405. - P. 244-248.
5. Филиппов Д.А. Низкочастотный и резонансный магнитоэлектрические эффекты в объемных композиционных структурах феррит никеля – цирконат - титанат свинца / Д.А. Филиппов, В.М. Лалетин, G. Srinivasan // Журнал технической физики. - 2012 - Т. 82 - №1 - С. 47-51.
6. Srinivasan G. Novel magnetoelectric bilayer and multilayer structures of magnetostrictive and piezoelectric oxides / G. Srinivasan, E.T. Rasmussen, J. Gallegos, R. Srinivasan, Yu. I. Bokhan, V.M. Laletin // Physical Review B. – 2001. – Vol.64. – P. 214408 (1-6).
7. Fetisov Y.K. Inverse magnetoelectric effects in a ferromagnetic-piezoelectric layered structure / Y.K Fetisov, V.M. Petrov, G. Srinivasan // J. Mater. Res. - 2007. - Vol. 22. - P.2074-2080.
8. Fetisov Y.K. Converse magnetoelectric effects in a galfenol and lead zirconate titanate bilayer / Y.K. Fetisov, K.E. Kamentsev, D.V. Chashin, L.Y. Fetisov, Srinivasan // Journal of Applied Physics. - 2009. - Т.105. - №12. - С.123918.
9. Филиппов Д.А. Магнитоэлектрический эффект в слоистых дискообразных магнитострикционно-пьезоэлектрических структурах: теория и эксперимент / Д.А. Филиппов, Г.С. Радченко, В.М. Лалетин // ФТТ. - 2016 - Т. 58 - №3. - С. 495-501.
10. Vopson M. Fundamentals of Multiferroic Materials / M. Vopson // Critical Reviews in Solid State and Materials Science. 2015. – Vol.40. - P. 223-250.
11. Filippov D.A. Influence of an interlayer bonding on the magnetoelectric effect in the layered magnetostrictive-piezoelectric structure / D.A. Filippov, T.A. Galichyan, V.M. Laletin // Appl. Phys. A. - 2014. - V. 116. - P. 2167-2171.
12. Филиппов Д.А. Магнитоэлектрический эффект в двухслойной магнитострикционно-пьезоэлектрической структуре / Д.А. Филиппов, В.М. Лалетин, T.A Galichyan // Физика твердого тела. - 2013. - Т. 55. - №9. - C. 1728-1733.
13. Filippov D.A. Magnetoelectric effect in bilayer magnetostrictive - piezoelectric structure. Theory and experiment / D.A. Filippov, V.M. Laletin, T.A. Galichyan // Applied Physics A. - 2014. - Vоl. 115. - P. 1087- 1091.
14. Филиппов Д.А. Технология изготовления и магнитоэлектрические свойства структур цирконат – титанат свинца – никель / Д.А. Филиппов, В.М. Лалетин, Т.О. Фирсова, О.В. Антоненков // Вестник Новгородского университета им. Ярослава Мудрого. – 2015. - № 6(89). - С. 100-104.
15. Фетисов Ю.К. Спинтроника: физические основы и устройства / Ю.К. Фетисов, А.С. Сигов //Радиоэлектроника. Наносистемы. Информационные технологии. - 2018. – Т. 10. – № 3. – С. 343-356.

Список литературы на английском языке / References in English

1. Bukharaev A. A. Strejntronika – novoe napravlenie mikro- i nanoehlektroniki i nauki o materialah [Straintronics: a new trend in micro- and nanoelectronics and materials science] / A. A. Bukharaev, A .K .Zvezdin, A. P. Pyatakov, Y. K.Fetisov // Physics - Uspekhi. – 2018. – Vol. 61(12). – P. 1175 -1212. [in Russian]
2. Zhang Highly efficient power conversion in magnetoelectric gyrators with high quality factor / J. Zhang, W. Zhu, D.A. Filippov, W. He, D. Chen, K. Li, S. Geng, Q. Zhang, L. Jiang, L. Cao, R. Timilsina, and G. Srinivasan // Rev. Sci. Instrum. – 2019. – Vol. 90. – P. 015004.
3. Zhang Bidirectional tunable ferrite-piezoelectric trilayer magnetoelectric inductors / J. Zhang, D. Chen, D. A. Filippov, K. Li, Q. Zhang, L. Jiang, W. Zhu, L. Cao, G. Srinivasan // Appl. Phys. Lett. – 2018. – Vol. 113. – P. 113502.
4. Burdin D.A. High-sensitivity DC field magnetometer using nonlinear resonance magnetoelectric effect / Burdin D.A., Chashin D.V., Ekonomov N.A., Fetisov Y.K., Stashkevich A.A. // Journal of Magnetism and Magnetic Materials. 2016. – Vol. 405. – P. 244-248.
5. Filippov D.A. Nizkochastotnyj i rezonansnyj magnitoehlektricheskie ehffekty v ob"emnyh kompozicionnyh strukturah ferrit nikelya – cirkonat - titanat svinca [Low Frequency and Resonance Magnetoelectric Effects in Nickel Ferrite–PZT Bulk Composites] / D.A. Filippov, V.M. Laletin, and G. Srinivasan // Technical Physics. - 2012. - Vol. 57. - N. 1. - P. 44–47. [in Russian]
6. Srinivasan G. Novel magnetoelectric bilayer and multilayer structures of magnetostrictive and piezoelectric oxides / G. Srinivasan, E.T. Rasmussen, J. Gallegos, R. Srinivasan, Yu. I. Bokhan, V.M. Laletin // Physical Review B. – 2001. – Vol.64. – P. 214408 (1-6).
7. Fetisov Y.K. Inverse magnetoelectric effects in a ferromagnetic-piezoelectric layered structure / Y.K Fetisov, V.M. Petrov, G. Srinivasan // J. Mater. Res. - 2007. - Vol. 22. - P.2074-2080.
8. Fetisov Y.K. Converse magnetoelectric effects in a galfenol and lead zirconate titanate bilayer / Y.K. Fetisov, K.E. Kamentsev, D.V. Chashin, L.Y. Fetisov, Srinivasan // Journal of Applied Physics. - 2009. - Vol.105. – N.12. - P.123918.
9. Filippov D.A. Magnitoehlektricheskij ehffekt v sloistyh diskoobraznyh magnitostrikcionno-p'ezoehlektricheskih strukturah: teoriya i ehksperiment [Magnetoelectric effect in layered disk-shaped magnetostrictive-piezoelectric structures: Theory and experiment] / D.A. Filippov, G.S. Radchenko, V.M. Laletin // Physics of the Solid State. - 2016. - Vol.58. - N. 3. - P. 508-514. [in Russian]
10. Vopson M. Fundamentals of Multiferroic Materials / M. Vopson // Critical Reviews in Solid State and Materials Science. 2015. – Vol.40. - P. 223-250.
11. Filippov D.A. Influence of an interlayer bonding on the magnetoelectric effect in the layered magnetostrictive-piezoelectric structure / D.A. Filippov, T.A. Galichyan, V.M. Laletin // Appl. Phys. A. - 2014. - V. 116. - P. 2167-2171.
12. Filippov D.A. Magnitoehlektricheskij ehffekt v dvuhslojnoj magnitostrikcionno-p'ezoehlektricheskoj strukture [Magnetoelectric Effect in a Magnetostrictive–Piezoelectric Bilayer Structure] / D. A. Filippov, V.M. Laletin, T.A. Galichyan // Physics of the Solid State. - 2013. - Vol. 55. - N. 9. - P. 1840–1845.
13. Filippov D.A. Magnetoelectric effect in bilayer magnetostrictive-piezoelectric structure. Theory and experiment / D.A. Filippov, V.M. Laletin, T.A. Galichyan // Applied Physics A. - 2014. - Vоl. 115, - P. 1087- 1091.
14. Filippov D.A. Technologiya isgotovleniya i magnitoelektricheskiye svoistva struktur zirkonat - titanat svinza - nikel' [The technology of fabrication and magnetoelectric properties of the structures zirconate – lead titanate – nickel] / D.A. Filippov, V.M. Laletin, T.O. Firsova, O.V. Antonenkov // Vestnik Novgorodskogo Universiteta im. Yaroslava Mudrogo [Bulletin of Novgorod University. Yaroslav The Wise] - 2015. - № 6 (89). - P. 100-104. [in Russian]
15. Fetisov Y.K. Spintronika: fizicheskie osnovy i ustrojstva [Spintronics: physical foundations and devices] / K. Fetisov, A.S. Sigov // RadioElectronics. NanoSystems. Information Technologies. - 2018. – Vol. 10. – N3. – P. 343-356