АЛГОРИТМ ПРЕДСТАВЛЕНИЯ СВОЙСТВ ОБЪЕКТОВ ЭКСПЕРТНОЙ СИСТЕМЫ
АЛГОРИТМ ПРЕДСТАВЛЕНИЯ СВОЙСТВ ОБЪЕКТОВ ЭКСПЕРТНОЙ СИСТЕМЫ
Научная статья
Гаджиев Ф.Г.1, Гулузаде Ф.И.2, *
1, 2 Азербайджанский Университет Нефти и Промышленности, Баку, Азербайджан
* Корреспондирующий автор (fuad_quluzade[at]mail.ru)
АннотацияРассматривается проблема представления свойств сложных объектов в базах знаний экспертных систем, когда они характеризуются неопределенностью и отсутствуют способы оценки каких либо значений размытости их количественных характеристик, что существенно затрудняет исследование соответствующего признакого пространства. Анализ поставленной задачи свидетельствует о целесообразности изначальной ориентации програмного обеспечения ее решения на многозначную интерпретацию с позиции нечеткого и лингвистического моделирования рассматриваемой проблемной области.
Ключевые слова: интеллектуальные системы, знания, экспертные системы, сложные объекты, нечеткость, функция принадлежности.
ALGORITHM FOR PRESENTING PROPERTIES OF EXPERT SYSTEM OBJECTS
Research article
Gadzhiev F.G.1, Guluzade F.I.2, *
1, 2 Azerbaijan State Oil and Industry University, Baku, Azerbaijan
* Corresponding author (fuad_quluzade[at]mail.ru)
AbstractThe article considers the problem of presenting the properties of complex objects in the knowledge bases of expert systems when they are characterized by uncertainty, and there is no other way to estimate ambiguity values of their quantitative characteristics, which complicates the study of the corresponding attribute space. The analysis of the task set testifies to the expediency of the initial orientation of the software for its solution to the multi-valued interpretation from the position of fuzzy and linguistic modeling of the problem area under consideration.
Keywords: intelligent systems, knowledge, expert systems, complex objects, fuzziness, membership function.Введение
Разработка экспертных систем часто предполагает наличие лингвистических характеристик и обычных операций, что непосредственно связано с целесообразностью построения таких систем на основе теории нечетких множеств, ориентированных на алгебру нечетких чисел. Под последними понимают нечеткое множество, которое определено на множестве действительных чисел и является выпуклой и унимодальной. К настоящему времени концепция интеллектуальных систем основывается большей частью, на такие современные научные направления, которые характеризуясь неточностью, неопределенностью и отсутствием стандартных средств решения поставленных задач, ориентированны на разработку систем, основанных на знаниях. Являясь системами искусственного интеллекта они создавались на базе программного обеспечения не содержащей интеллектуальные элементы с одной стороны и эффективные процедуры численных методов, концептуально противоречащих интеллектуальным особенностям этих систем [1], [2].
Следует иметь ввиду очевидное присутствие интеллектуальности практически во всех задачах искусственного интеллекта, отсутствие возможности моделирования которых стандартными математическими формализмами в полной мере ориентировано на многозначную интерпретацию, увязываются к концепции нечетких множеств и моделей. Последняя обеспечивает реализацию нечетких рассуждений и принятие решений в различных проблемных областях, к примеру, системах планирования при нечеткой исходной информации, процессах управления техническими и другими системами, экспертных системах. При этом предпринимаются попытки расширения понятия нечеткости как такового, а традиционный анализ нечетких свойств объектов обобщается на формализацию классического понимания неопределенности и плохоструктрированности [3], [4].
Исследования свойств объектов экспертной системы способствуют экспертной и системной интерпретации характеристик изучаемого пространства ![]() . При этом особое значение приобретает анализ их операционных значений, так как интенсивная проработка знаний в интеллектуалных системах с учетом алгоритмов реализации обычных арифметических операций и обобщение считаются эффективным средством обеспечение ее актуальности.
. При этом особое значение приобретает анализ их операционных значений, так как интенсивная проработка знаний в интеллектуалных системах с учетом алгоритмов реализации обычных арифметических операций и обобщение считаются эффективным средством обеспечение ее актуальности.
Постановка задачи
Пусть на формальном статическом пространстве 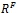 регулярной сетью задано множество сложных объектов
регулярной сетью задано множество сложных объектов
![]()
которым ставят в соответствие свойства заданные в виде матрицы
![]() ; j - ое свойство i - го объекта. Поскольку матрица отображает ее строки и столбцы
; j - ое свойство i - го объекта. Поскольку матрица отображает ее строки и столбцы
![]()
то она полностью соответствует пространству 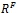 , а следовательно характеризует ее текущее состояние. Требуется произвести идентификацию свойств объектов лингвистическими характеристиками.
, а следовательно характеризует ее текущее состояние. Требуется произвести идентификацию свойств объектов лингвистическими характеристиками.
Методы решения
Решение поставленной задачи тесно связано с пониманием важности проблемы представления знаний соответствующих сложным объектам, поскольку будучи плохоструктурированными не содержат в себе систематических процедур, а решение представляется в виде поиска в пространстве состояний, характеризующихся нечеткими значениями ее информационных единиц. Последние могут быть интерпретируемы лингвистическими характеристиками на основе следующего алгоритма:
- Активизация стартового состояние базы знаний экспертной системы.
- Выбор исследуемых свойств объектов.
- Активизация процедуры формирования лингвистической шкалы.
- Подключение аппроксимационных процедур.
- Задание функций принадлежности и α-уровня. Генерация терм-множества и лингвистических характеристик объектов.
Важнейшей характеристикой данного алгоритма является поиск эффективного определения функции принадлежности, что реализовано нами следующим алгоритмом:
- Активизация буферной зоны базы знаний содержащей лингвистические характеристики, определенные на основе предыдущего алгоритма.
- При системном задании функции принадлежности перейти к 5.
- Если рассматриваемый лингвистический терм «очень малое», то
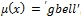 , иначе, если «малое», то
, иначе, если «малое», то 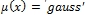 , иначе если «среднее», то
, иначе если «среднее», то 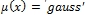 , иначе если «большое», то
, иначе если «большое», то 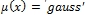 , иначе если «очень большое», то
, иначе если «очень большое», то 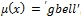 (по обозначении MATLAB).
(по обозначении MATLAB). - Идти к 6.
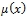 и лингвистический терм заданы системно.
и лингвистический терм заданы системно.- При продолжении алгоритма идти к 2.
В алгоритме могут быть использованы различные классы функций принадлежности, среди которых особое место занимают экспоненциальные:

Следует иметь в виду что рассмотренный алгоритм характеризуется тем, что допускает вмешательство эксперта или не системных процедур. Однако при решении определенного класса задач подобное вмешательство не поддерживается экспертами по следующим причинам:
- основное внимание сосредаточено на подцелях, а остальные вопросы должны быть реализованы системно;
- эксперт в текущей ситуации не распологает знаниями о появившейся проблеме;
- во многих случаях пользователи не считают целесообразным вмешиватся во все технические детали;
Исходя из этого представление элементов терм-множества может производится алтернативными способами, например на основе квадратичных функций:
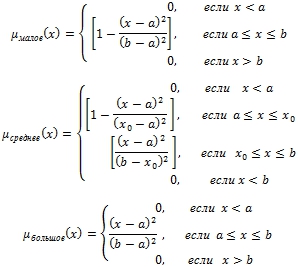
Данный алгоритм определен следующим образом:
- Загрузка системы.
- Определение характеристик пространства признаков.
- Вычисление граничных и промежуточных значений лингвистической шкалы.
- Вычисление степеней принадлежности, причем при непересекающемся интервале производится прямое определение величины принадлежности, а при пересекающемся интервале первоначально устанавливается ближайшая граница, после чего степень принадлежности вычисляется относительно значения этой границы. В равноудаленном случае преимущественнее считается правая граница.
- Организация вывода.
На основе приведенных алгоритмов разработано программное обеспечение, которое было апробировано на материалах космических исследований. Исходная, прямоугольная матрица T была сформирована четырьмя свойствами указанных материалов, а относительно одного свойства были получены следующие результаты.
Таблица 1 – Свойства объектов со степенями принадлежности

Заключение
В результате проведенных исследований установлены приемлемые алгоритмы идентификации свойств сложных объектов с нечетких позиций, которые могут быть реализованы не только в случае экспертного или системного задания значений лингвистической переменной, но и в ситуации их отсутствия, когда терм-множество формируется на основе системных процедур.
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Алиев А.А. Soft computing. Часть первая / Алиев А.А., Алиев Р.Р. Баку, АГНА, 1999, 181 с.
- Zadeh L.A. Fuzzy sets: Inform. and control / Zadeh L.A., 1965, N8, pp. 338-353.
- Stuart J. Russel Artficial Intelligence. A Modern Approach / Stuart J. Russel, Peter Norvig. Prentice Hall. Upper Saddle River. New Jersey 074458, 2005, 1408 p.
- Zohri A. Continuity of fuzzy sets approximate additive mappings / Zohri A., Eghbali N.. Jour Pure Appl. Math, V3, N1, 2013, A 35-40.
- Borisov A.N. Methods for interactive evaluation of solutions / Borisov A.N., Levchenko A.S.. Riga, Zinatne, 1982, 180 p.
- Mirmostafaee A.K. Fuzzy almost quadratic functions. Results in Math / Mirmostafaee A.K., Moslehian M.S., 52, 2008, p. 161-177.
- Кофман А. Введение в теорию нечетких множеств / Кофман А. М., Радиосвязь, 1982, 432 с.
- Jager R.R. Fuzzy sets, neural networks and Soft Computing, VAN Nostrand Reinhold / Jager R.R., Zadeh L.A., New York 1994, 440 p.
- Həsənov G. Fazzi riyaziyyat idarəetmə modellərində / Həsənov G. Bakı, Elm, 2000, 454 s.
- Presentation of uncertain information with help of canonically conjugate fuzzy subsets. 4th international conference problems of Cybernetics and Informatics (PCI), 2012.
Список литературы на английском языке / References in English
- Aliyev A.A. Soft computing. First Part / Aliyev A.A., Aliyev R.R.. Baku, ASOA, 1999, 181 p.
- Zadeh L.A. Fuzzy sets: Inform. and control / Zadeh L.A., 1965, N8, pp. 338-353.
- Stuart J. Russel Artficial Intelligence. A Modern Approach / Stuart J. Russel, Peter Norvig.. Prentice Hall. Upper Saddle River. New Jersey 074458, 2005, 1408 p.
- Zohri A. Continuity of fuzzy sets approximate additive mappings / Zohri A., Eghbali N. Jour Pure Appl. Math, V3, N1, 2013, P 35-40.
- Borisov A.N. Methods for interactive evaluation of solutions / Borisov A.N., Levchenko A.S. Riga, Zinatne, 1982, 180 p.
- Mirmostafaee A.K. Fuzzy almost quadratic functions / Mirmostafaee A.K., Moslehian M.S. Results in Math, 52, 2008, p. 161-177.
- Kofman A. Vvedenie v teoriyu nechetkih mnozhestv [Introduction to the theory of fuzzy sets] / Kofman A. M., Radiosvyaz, 1982, 432 p. [in Russian]
- Jager R.R. Fuzzy sets, neural networks and Soft Computing, VAN Nostrand Reinhold / Jager R.R., Zadeh L.A., New York 1994, 440 p.
- Hasanov G. Fuzzy math in management models. Baku, Elm, 2000, 454
- Presentation of uncertain information with help of canonically conjugate fuzzy subsets. 4th international conference problems of Cybernetics and Informatics (PCI), 2012.
