РЕШЕНИЕ НЕКЛАССИЧЕСКИХ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ ВОЛЬТЕРРА I РОДА С ВЫРОЖДЕННЫМ НЕЛИНЕЙНЫМ ЯДРОМ
1Доктор физико-математических наук,
Кыргызко-Турецкий университет «Манас»;
2Старший преподаватель,
Ошский государственный университет, Республика Кыргызстан
РЕШЕНИЕ НЕКЛАССИЧЕСКИХ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ ВОЛЬТЕРРА I РОДА С ВЫРОЖДЕННЫМ НЕЛИНЕЙНЫМ ЯДРОМ
Аннотация
Интегральные уравнения относятся к разделу математики. Важным из приложений является то, что к ним приводится большое число задач из самых разных разделов физики, техники и других наук. В связи с этим в последние годы теория интегральных уравнений бурно развивается благодаря трудам многих исследователей.
Однако уравнения с двумя переменными пределами интегрирования, которые называют неклассическими, мало изучены. Это, наверно, объясняется трудностями в построении резольвенты и в составлении соотношения для нее, т.к. еще не получено аналитическое представление в общем виде за исключением некоторых модельных случаев.
Ключевые слова: интегральное уравнение, формула Дирихле, малый параметр, двойные интегралы.
Asanov A.A.1, Choyubekov S.M.2
1PhD in Physics and Mathematics,
Kyrgyz-Turkey Manas University;
2Senior Lecturer,
Osh State University, Kyrgyz Republic
SOLUTION OF NONCLASSICAL INTEGRAL VOLTERRA EQUATIONS OF FIRST KIND WITH DEGENERATE NONLINEAR KERNEL
Abstract
Integral equations relate to the branch of mathematics, the important thing of which is that a large number of problems a wide range of sections of physics, engineering, and other sciences are reduced to them. Because of this, in recent years the theory of integral equations has been developing rapidly due to the work of many researchers.
However, equations with two variable limits of integration, which are called non-classical, have been little studied.
This is probably due to the difficulties in constructing of resolvent and in constructing a correlation for it since the analytical representation in general form has not yet been obtained except for some model cases.
Keywords: integral equation, Dirichlet formula, small parameter, double integrals.
Интегральные уравнения относятся к разделу математики, важным из приложений является то, что к ним приводится большое число задач из самых разных разделов физики, техники и других наук. В связи с этим в последние годы теория интегральных уравнений бурно развивается благодаря трудам многих исследователей [1], [10].
Однако уравнения с двумя переменными пределами интегрирования, которые называют неклассическими мало изучены. Это, наверно, объясняется трудностями в построении резольвенты и в составлении соотношения для нее, т.к. еще не получено аналитическое представление в общем виде за исключением некоторых модельных случаев.
В данной работе в предположении, что ![]() , следуя по методу, предложенному М. Иманалиевыми, А. Асановым [8], устанавливаются достаточные условия регуляризации решения неклассического интегрального уравнения Вольтерра I рода.
, следуя по методу, предложенному М. Иманалиевыми, А. Асановым [8], устанавливаются достаточные условия регуляризации решения неклассического интегрального уравнения Вольтерра I рода.
Рассмотрим
![]() (1)
(1)
где ![]() – заданные функции на отрезке
– заданные функции на отрезке ![]() и в области
и в области ![]() , – искомая функция на отрезке
, – искомая функция на отрезке ![]() .
.
Пусть
![]() (2)
(2)
где ![]() – решение уравнения (3), а
– решение уравнения (3), а ![]() – неизвестная функция
– неизвестная функция
Подставляя (4) из (3) получим
![]() (6)
(6)
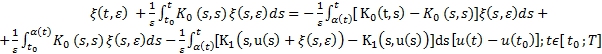 (7)
(7)
Используя резольвенту ![]() ядра
ядра ![]() и считая правую часть известным, решение (7) можно представить в следующем виде
и считая правую часть известным, решение (7) можно представить в следующем виде
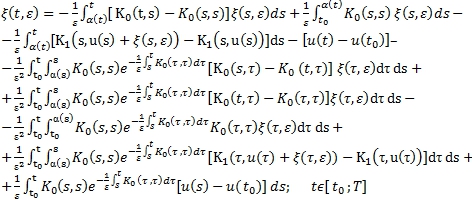 (8)
(8)
Вычислим двойные интегралы, при этом воспользуемся формулой Дирихле и будем иметь ввиду, что ![]() ,
,
Тогда из (6) получится
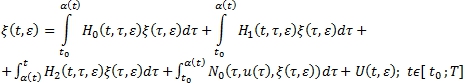 (9)
(9)
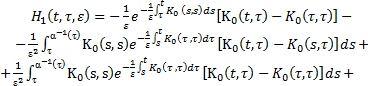 (11)
(11)
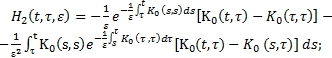 (12)
(12)
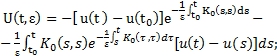 (14)
Потребуем выполнения следующих условий:
(14)
Потребуем выполнения следующих условий:
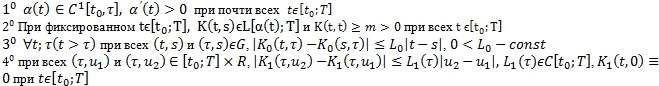
Обозначим ![]() – пространство Гольдера, т.е. функция
– пространство Гольдера, т.е. функция ![]() определенная в
определенная в ![]() удовлетворяет условию
удовлетворяет условию
![]() (15)
(15)
Здесь ![]() – некоторая постоянная, зависящая от
– некоторая постоянная, зависящая от ![]() , но не от t и τ. Ещё установлено, что
, но не от t и τ. Ещё установлено, что ![]() является Банаховым пространством с нормой
является Банаховым пространством с нормой
![]() (16)
(16)
Далее установим справедливость следующих утверждений:
Лемма 1
Если выполняются условия ![]() . Тогда для функции
. Тогда для функции ![]() определенной по формуле (8), имеет место
определенной по формуле (8), имеет место
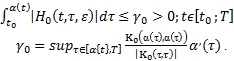 (17)
Доказательство:
(17)
Доказательство:
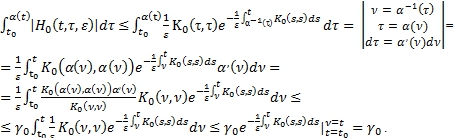
Доказано.
Лемма 2
Пусть и определены по формулам (9), (10) соответственно. Кроме того, выполняются условия ![]() Тогда справедливы оценки:
Тогда справедливы оценки:
![]()
![]() (18)
(18)
![]() (19)
(19)
Доказательство
Имея ввиду ![]() и воспользовавшись формулой интегрирования по частям, получаем соответствующие оценки.
и воспользовавшись формулой интегрирования по частям, получаем соответствующие оценки.
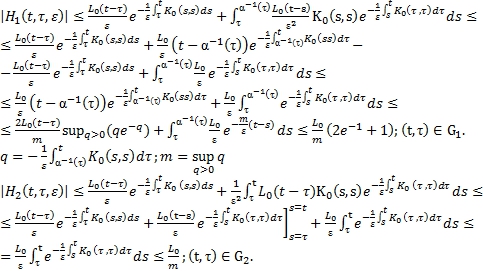 (20)
(20)
Лемма 3
Пусть выполняются условия ![]() функция
функция ![]() определена соответственно формулой (11). Тогда имеют место следующие неравенства
определена соответственно формулой (11). Тогда имеют место следующие неравенства
![]() (21)
(21)
![]() (22)
(22)
Доказательство
Если переходить к оценке в (11) соответственно с учетом условий леммы, заметив ![]() получаем требуемые оценки.
получаем требуемые оценки.
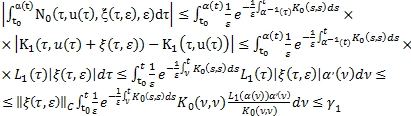
Лемма 4
Пусть ![]()
Тогда 1). Если ![]() при почти всех
при почти всех ![]() и
и ![]() справедлива оценка
справедлива оценка

Итак, сформулируем основные результаты:
Теорема 1
Пусть выполняются условия ![]()
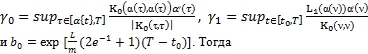
1) если уравнение (1) имеет решение ![]() , то решение
, то решение ![]() уравнения (3) при
уравнения (3) при ![]() сходится по норме C
сходится по норме C![]() к решению
к решению ![]() и справедлива оценка
и справедлива оценка
![]() (24)
(24)
где ![]()
2) если уравнение (1) имеет решение ![]() , то решение
, то решение ![]() уравнения (3) при
уравнения (3) при ![]() сходится по норме C
сходится по норме C![]() к решению u(t). При этом справедлива оценка
к решению u(t). При этом справедлива оценка
![]() (25)
(25)
где ![]()
Доказательство
В силу лемм 1-4 из уравнения (7) имеем
![]() (26)
(26)
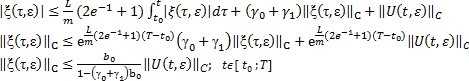 Теорема 1 доказана.
Теорема 1 доказана.
Список литературы / References
- Чоюбеков С.М. Регуляризация решения неклассического интегрального уравнения с условиями Липшица / Чоюбеков С.М. // Молодой ученый. - Казань. - № 8 (112) – 2016 - с. 34-37
- Чоюбеков С.М. Об одном классе неклассического интегрального уравнения Вольтерра I рода / Чоюбеков С.М., Бекешов Т.О., Асанов А. // Вестник № 3 Ошского государственного университета - Ош - 2014 - с. 83-88
- Чоюбеков С.М. О решение неклассического интегрального уравнения I рода в пространстве непрерывных функции / Асанов А., Бекешов Т.О., Чоюбеков С.М. // Вестник № 3, Ошского государственного университета – Ош – 2012 - с. 48-54
- Асанов А. Регуляризация и единственность решения неклассического интегрального уравнения с условиями Липшица / Асанов А., Бекешов Т.О., Чоюбеков С.М. // Вестник спец.вып. КНУ имени Ж. Баласагына – Бишкек – 2011 - с. 108-111
- Бекешов Т.О. Единственность решения интегрального уравнения Вольтерра первого рода с двумя независимыми переменными / Асанов А., Бекешов Т.О. // Материалы Междунар. Конф. «Актуальные проблемы математики и математические моделирования экологических систем», октябрь, 1996 – Алматы.
- Апарцин А.С. Неклассические уравнения Вольтерра I рода: Теория и численные методы / Апарцин А.С. // Новосибирск: Наука, Сибирское отделение – 1999 - 193 с.
- Апарцин А.С. Применения интегральных уравнений Вольтерра для моделирования стратегий технического перевооружения электроэнергетики / Апарцин А.С., Караулова И.В., Маркова Е.В. и др. // Электричество, 2005 - № 10 - С. 69-75
- Асанов А. О решениях систем нелинейных двумерных интегральных уравнений Вольтера первого рода / Иманалиев М.И., Асанов А. // ДАН 1991 - Т. 317. № 1. - С. 32-35
- Иманалиев М.И. Регуляризация, единственность и существование решения для интегральных уравнений Вольтерра I- рода / Иманалиев М.И., Асанов А. // Исс. по инт-дифф. Урав-м – Фрунзе: Илим 1988, - Вып.21 - С.3-38
- Лаврентьев М.М. Некорректные задачи математической физики и анализа / Лаврентьев М.М., Романов В.Г., Шишатский С.Р. // М: Наука, 1980.
Список литературы на английском языке / References in English
- Choyubekov S.M. Regulyarizatsiya resheniya neklassicheskogo integral'nogo uravneniya s usloviyami Lipshitsa [Regularization of Solution of Nonclassical Integral Equation under Lipschitz Conditions] / Choyubekov S.M. // Molodoj uchenyiy [Young Scientist]. – Kazan - No. 8 (112) – 2016 - pp. 34-37 [in Russian]
- Choyubekov S.M. Ob odnom klasse neklassicheskogo integral'nogo uravneniya Vol'terra I roda [On Class of Nonclassical Integral Volterra Equation of First Kind] / Choyubekov S.M., Bekeshov T.O., Asanov A. // Bulletin No. 3 of Osh State University. Osh, 2014, pp. 83-88 [in Russian]
- Choyubekov S.M. O resheniye neklassicheskogo integral'nogo uravneniya I roda v prostranstve nepreryvnykh funktsii. [On solution of Nonclassical Integral Equation of First Kind in Space of Continuous Functions] / Asanov A., Bekeshov T.O., Choyubekov S.М. // Bulletin No. 3, Osh State University, Osh, 2012, pp. 48-54 [in Russian]
- Asanov A. Regulyarizatsiya i yedinstvennost' resheniya neklassicheskogo integral'nogo uravneniya s usloviyami Lipshitsa [Regularization and Uniqueness of Solution of Nonclassical Integral Equation under Lipschitz Conditions] / Asanov A., Bekeshov T.O., Choyubekov S.М. // Bulletin, special issue of KNU named after J. Balasagyn. Bishkek, 2011, pp. 108-111 [in Russian]
- Bekeshov T.O. Yedinstvennost' resheniya integral'nogo uravneniya Vol'terra pervogo roda s dvumya nezavisimymi peremennymi [Uniqueness of Solution of Volterra Integral Equation of First Kind with Two Independent Variables] / Asanov A., Bekeshov T.O. // Materials of Intern. Conf. "Topical problems of mathematics and mathematical modeling of ecological systems" – Almaty, 1996 [in Russian]
- Apartsin A.S. Neklassicheskiye uravneniya Vol'terra I roda: Teoriya i chislennyye metody [Nonclassical Volterra Equations of First Kind: Theory and Numerical Methods] / Apartsin A.S. // Novosibirsk: Science, Siberian Branch, 1999.-193 p [in Russian]
- Apartsin A.S. Primeneniya integral'nykh uravneniy Vol'terra dlya modelirovaniya strategiy tekhnicheskogo perevooruzheniya elektroenergetiki [Applications of Integral Volterra Equations for Modeling Strategies for Technical Re-equipment of Electric Power Industry] / Apartsin A.S., Karaulova I.V., Markova E.V. and others // Electricity, 2005, - No. 10 – P. 69-75 [in Russian]
- Asanov A. O resheniyakh sistem nelineynykh dvumernykh integral'nykh uravneniy Vol'tera pervogo roda [On solutions of systems of nonlinear two-dimensional Voltaire integral equations of the first kind] / Imanaliev M.I., Asanov A. // DAN 1991. 317. No. 1. P. 32-35 [in Russian]
- Imanaliev M.I. Regulyarizatsiya, yedinstvennost' i sushchestvovaniye resheniya dlya integral'nykh uravneniy Vol'terra I- roda [Regularization, Uniqueness and Existence of Solution for Volterra Integral Equations of First Kind] / Imanaliev M.I., Asanov A. // Iss. by int.-diff. Urav-m – Frunze: Ilim 1988. – Is.21 – P.3-38 [in Russian]
- Lavrentyev M.M. Nekorrektnyye zadachi matematicheskoy fiziki i analiza [Inadequate Problems of Mathematical Physics and Analysis] / Lavrent'ev M.M., Romanov V.G., Shishatskii S.R. // M: Science, 1980 [in Russian]
