ОСОБЕННОСТИ ШАРНИРНЫХ ОПОРНЫХ УЗЛОВ БОЛЬШЕПРОЛЕТНЫХ КОНСТРУКЦИЙ

Вержбовский Г.Б.¹, Сухомлинов А.С.²

¹ORCID: 0000-0002-8412-2675, Доктор технических наук,

²Магистрант,

^1,2Академия строительства и архитектуры Донского государственного технического университета, г. Ростов-на-Дону

ОСОБЕННОСТИ ШАРНИРНЫХ ОПОРНЫХ УЗЛОВ БОЛЬШЕПРОЛЕТНЫХ КОНСТРУКЦИЙ

Аннотация

Рассмотрены отечественный и зарубежный варианты опорных узлов большепролетных конструкций в виде балансирных шарниров. Выполнены их аналитические и численные расчеты. Показано, что решение контактных задач в рассматриваемом случае приводит к несколько заниженным результатам по сравнению с данными численного эксперимента над твердотельной моделью. Делается вывод о том, что теория, рассматривающая давление штампа на упругую полуплоскость или пространство, не соответствует реальной конструкции опоры. Отмечены преимущества зарубежного варианта балансира, конструкция которого наиболее близка к идеальному шарниру расчетной схемы.

Ключевые слова: балансир, цапфа, контактная задача, твердотельная модель.

Verzhbovskiy G.B.¹, Sukhomlinov A.S.²

¹ORCID: 0000-0002-8412-2675, PhD in Engineering,

²Master’s degree student,

^1,2Academy of Construction and Architecture of Rostov State Technical University of Civil Engineering, Rostov-on-Don

FEATURES OF SWIVEL SUPPORT NODES OF LONG SPAN STRUCTURES

Abstract

The domestic and foreign options of support assemblies of large span structures in the form of swivel hinges are considered. Their analytical and numerical calculations are performed. It is shown that the solution of the contact problems in the case under consideration leads to a little lower result compared with data of the numerical experiment on the solid model. It is concluded that a theory, considering the pressure of a stamp on an elastic half-plane or space does not correspond to the actual construction of the support. The advantages of the foreign version of the rocker, the construction of which is the closest to the ideal hinge of the design scheme, are noted.

Keywords: balance arm, trunnion, contact problem, solid model.

При расчете соединений элементов строительных конструкций, как правило, вводится ряд допущений, упрощающих оценку напряженно-деформированного состояния узла и сводящихся к представлению последнего в виде идеального шарнира или жесткой заделки [1]. Для обычных зданий и сооружений подобный подход вполне оправдан, поскольку не оказывает серьезного влияния на конечный результат. Однако в связи с тем, что в последнее время у нас в стране все большее распространение получают большепролетные конструкции, упрощения узловых соединений могут привести к серьезным проблемам. Одним из возможных решений указанной проблемы может стать конструирование соединений, близких к идеальным узлам расчетных схем.

Опорные части конструкций являются наиболее ответственными, поскольку на них приходится вся нагрузка от вышележащих элементов здания, а также технологические и природно-климатические воздействия. Рассмотрим в настоящей статье в качестве примера шарнирную опору большепролетных арок или рам, выполненных из стали. В учебной литературе по металлическим конструкциям [2] приводятся три возможных варианта узлов – пятниковый, плиточный и балансирный. Наиболее близким к реальному шарниру следует считать именно балансирный. За рубежом два первых варианта из перечисленных выше узлов практически не применяются, а что касается последнего, то его конструкция несколько отличается от российской.

Отечественный вариант шарнира (см. рис. 1), состоит из верхнего и нижнего балансиров, в гнезда которых укладывают плотно пригнанную цилиндрическую цапфу. Опорную часть большепролетной конструкции прикрепляют к верхнему балансиру через плиту и притягивают болтами к балансиру. С учетом допускаемого давления на фундамент нижний балансир обычно имеет большую площадь опирания, чем верхний. Для восприятия отрицательных опорных реакций от действия ветра легкие и высокие конструкции крепятся к опорам анкерными болтами.

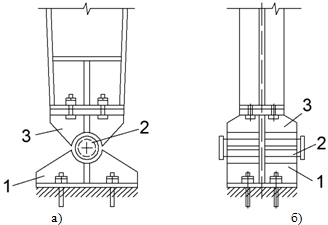
Рис. 1 – Конструктивная схема балансирного шарнира вид спереди а) и сбоку б): 1 – плита; 2 – цапфа; 3 – балансир

 

Принцип работы узла заключается в том, что вертикальная составляющая сосредоточенной силы от верхнего балансира 3 передается на цапфу 2, которая в свою очередь передает нагрузку на нижний балансир 3.

В случае равенства диаметров цапфы и выемки нижнего балансира нагрузка от цапфы распределяется по выемке на всю ее длину, в результате чего возникают нормальные напряжения от границ выемки до вертикальной оси, проходящей через центр тяжести цапфы, что иллюстрируется пунктирной линией (см. рис. 2). На практике оказывается, что для обеспечения возможности поворота конструкции на опоре указанные выше диаметры не совпадают, поэтому зона касания становится меньше, а максимальное напряжение возрастает (сплошная линия на рисунке 2).

Аналитическое определение максимальной величины, а также ширины зоны распределения эпюры давления можно отыскать по приближенной методике, изложенной в [3], [4]. Воспользуемся полученными в указанном источнике решениями и запишем выражения для полуширины полоски контакта b и величины наибольшего давления между соприкасающимися телами p₀ соответственно:

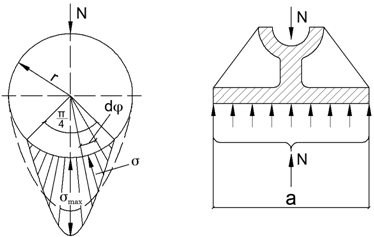
Рис. 2 – Расчетная схема балансирного шарнира

   (1)

При выводе (1) принято, что оба тела выполнены из одного и того же материала, с модулем упругости Е и коэффициентом Пуассона ν=0,3, что соответствует стали, из которой обычно и выполняют детали балансирного шарнира. q – это погонная нагрузка на единицу длины цилиндра.

Преобразуем выражения (1). Для этого подставим вместо обозначения модуля упругости E его конкретное значение и введем величину r=│ R₁ / R₂ │≥1. В реальных балансирных шарнирах радиусы цапфы и выемки балансира отличаются на весьма небольшую, но все-таки отличную от нуля величину, поэтому можно утверждать, что 1,001 ≤ r ≤ 1,01, тогда (1) приводится к окончательному виду:

  (2)

где  числовые значения γ при разных величинах r приведены в таблице 1.  

Таблица 1 – Числовые значения γ при разных величинах r

r	1,001	1,002	1,003	1,004	1,005	1,006	1,007	1,008	1,009	1,01
γ	1001	501	334	251	201	168	144	126	112	101

 

Рассмотрим в качестве примера балансирный шарнир, диаметр цапфы которого составляет d = 10см, при ее длине l = 10см, радиус выемки балансира на 0,1мм больше радиуса цапфы – 5,05см, а погонная нагрузка q = 1кН/см. При таких исходных данных имеем: r = 1,01, γ = 1,01, b = 2,4см, р₀ = 13,35кН/см². Если учесть, что b – это полуширина площадки контакта, то оказывается, что длина дуги, по которой распределено давление от цапфы, составляет 4,8см, что соответствует центральному углу, равному 55⁰. Полученное значение неплохо согласуется с показанным на рисунке 2 центральным углом 45⁰, однако в связи с очевидной приближенностью результата требует проверки.

Рассмотрим теперь шарнирные узлы другой конструкции, широко применяемые за рубежом (см. рис. 3). Их отличительной особенностью является то, что гнездо для размещения цапфы в балансирах представляет собой не дугообразную выемку, а кольцо. Конструкция соединения при этом оказывается несколько более материалоемкой, однако она, по сути, и является тем самым неподвижным шарниром, который принимается проектировщиками в расчетных схемах большепролетных сооружений.

Аналитический расчет подобных контактных задач достаточно подробно изложен в литературе по машиностроению, например, [5-8]. Речь идет о задаче о внутреннем контакте при неограниченном охватывающем теле. Внутренний контакт рассматривается как вдавливание круговой цапфы в тело с круглой полостью, которое после приложения нагрузки касается цапфы по сравнительно большому участку [5].

Рис. 3 – Шарнирная опора моста

 

Выражение, описывающее распределение давления в данном случае, возможно представить в виде (3):

      (3)

Коэффициенты a₁, a₂ и предельный угол эпюры давления  можно определить по графикам, приведенным в [5]. В условиях рассмотренного выше примера получим

Последнее значение оказывается близким к найденному по (2). Тем не менее, поскольку теоретические выкладки являются приближенными, был выполнен численный эксперимент над твердотельными моделями узлов. Для этой цели использовались возможности программного комплекса SolidWorks [9, 10].

На рисунке 4 показаны нижний балансир и половина цапфы модели отечественного узла.

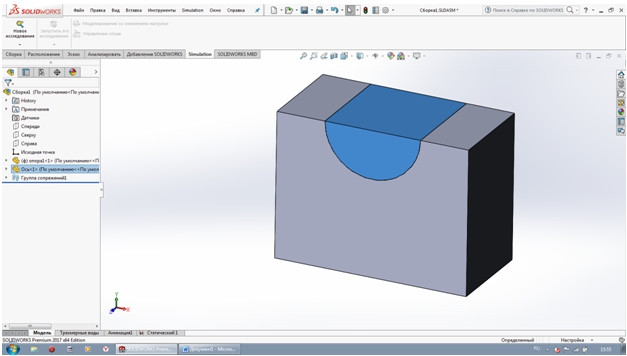
Рис. 4 – Модель отечественного балансирного шарнира

 

Как видно из указанного рисунка центральный угол раскрытия выемки балансира составляет 180⁰. В реальных строительных конструкциях для обеспечения возможности поворота отдельных элементов узла друг относительно друга угол раскрытия должен быть менее 180⁰, поэтому рассматривались три варианта балансирного шарнира с различными углами раскрытия выемки. Для удобства корректировки нижнего балансира от него «отрезалась» верхняя часть, что обеспечивало уменьшение угла раскрытия. Общий вид балансира с обрезанной частью и обозначениями основных размеров показан на рисунке 5. Очевидно, что величина центрального угла раскрытия выемки при таких условиях может быть определена по формуле

   (4)

В рассмотренных случаях при a = 15 и 30мм имеем α = 163⁰ и 147⁰ соответственно.  

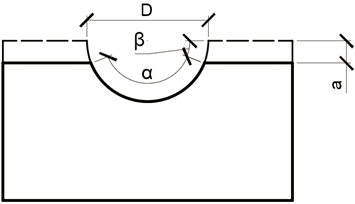
Рис. 5 – К определению величины угла раскрытия выемки

 

В результате статического расчета трех вариантов узла получены схемы распределения напряжений в нижнем балансире. Для угла раскрытия 180⁰ эпюра давления (см. рис. 6) несколько отличается от полученной выше в результате аналитического расчета аналогичного узла. Тем не менее, из указанного рисунка видно, что давление гасится внутри балансира и не выходит на его границы.

Величина максимального давления для балансира с углом раскрытия 180⁰ оказывается равным 20,61кН/см², что несколько больше аналитических значений.

Совершенно иная ситуация возникает при меньших величинах угла раскрытия выемки (см. рис. 7). Здесь имеет место концентрация напряжений в местах начала выемки, что может привести к недопустимым деформациям балансира в реальных строительных конструкциях.

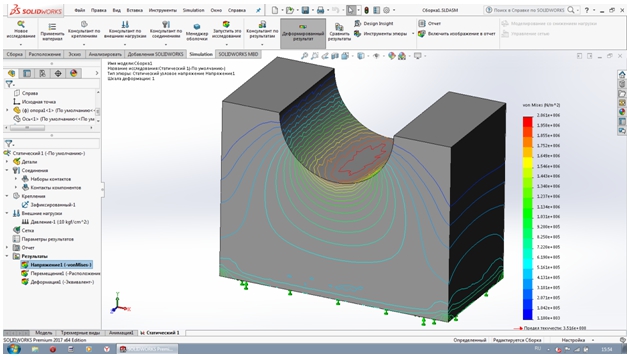
Рис. 6 – Эпюра давления для балансира с раскрытием гнезда 180^о

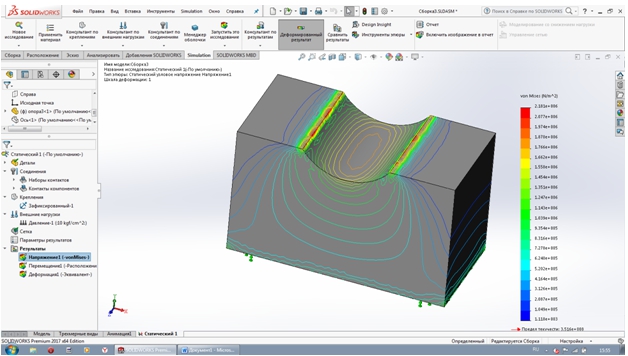
Рис. 7 – Эпюра давления для балансира с раскрытием гнезда 147^о

 

Таким образом, «российский» вариант конструкции балансирного шарнира обладает не только чисто конструктивными недостатками, но и оказывается неудачным с позиций статики. Появление концентраторов напряжений может привести к возникновению нештатных ситуаций.

Что касается формы эпюры давления, то она отличается от полученной аналитическим путем. Частично отличие можно объяснить тем, что в аналитическом решении рассматривается давление штампа на упругую полуплоскость, бесконечно продолжающуюся в направлении ниже выемки, а в реальных строительных конструкциях размер балансира является ограниченным. Факт несовпадения форм эпюр требует более глубокого дополнительного изучения и в рамках настоящего исследования не рассматривается.

При рассмотрении зарубежного варианта узла получен результат (см. рис. 8).

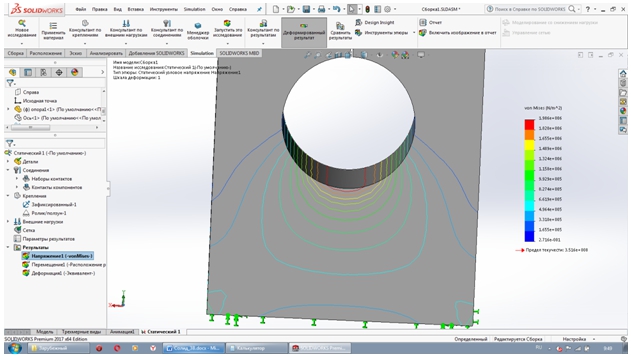
Рис. 8 – Распределение напряжений в охватывающем теле

 

Величина максимального напряжения оказалась равной 19,86кН/см².

Полученные в настоящем разделе аналитические и численные результаты для наглядности сведены в таблицу 2.

 

Таблица 2 – Результаты аналитического и численного расчета

Вариант решения	Аналитические результаты		Численные результаты
	Контактная задача, решение по [4]	Контактная задача, решение по [5]	Российский вариант узла	Зарубежный вариант узла
Максимальное давление р0, кН/см2	13,35	14,46	20,61	19,86

 

Как видно из этой таблицы приближенные аналитические решения дают несколько заниженный результат. Также необходимо учитывать тот факт, что конструкция охватывающих цапфу балансиров имеет свои особенности и не может считаться телом бесконечных размеров.

Список литературы / References

1. Штаерман И. Я. Контактная задача теории упругости / И. Я. Штаерман. – М.: Гостехтеориздат, 1949. – 272 с.
2. Кудишин Ю. И. Металлические конструкции / Ю. И. Кудишин, Е. И, Беленя. – 13-е изд. – М.: Академия, 2011. – 688 с.
3. Сухарев И. П. Прочность шарнирных узлов машин / И. П. Сухарев. – М.: Машиностроение, 1977. – 168 с.
4. Пановко Я. Г. Прочность, устойчивость, колебания. В 3 т. Т.2. / Я. Г. Пановко, И. А. Биргер. – М.: Машиностроение, 1968. – 383-393 с.
5. Александров В. М. Контактные задачи в машиностроении / В. М. Александров, Б. Л. Ромалис. – М.: Машиностроение, 1986. – 29-31 с.
6. Александров В. М. Контактные задачи для тел с тонкими покрытиями и прослойками / В. М. Александров, С. М. Мхитарян. – М.: Наука, 1983. – 488 с.
7. Попов Г. Я. Концентрация упругих напряжений возле штампов, разрезов тонких включений и подкреплений / Г. Я. Попов. – М.: Наука, 1982. –344 с.
8. Теплый М. И. Контактные задачи для областей с круговыми границами / М. И. Теплый. – Львов: Вища школа, 1983. – 176 с.
9. Bethune J.D. Engineering Design and Graphics with SolidWorks 2016 – Peachpit Press, 2016. — 784 p.
10. Planchard D. Official Certified SolidWorks Professional (CSWP) Certification Guide with Video Instruction: SolidWorks 2012-2014 - SDC Publications, 2014. – 192 p.

Список литературы на английском языке / References in English

1. Shtaerman I. Ya. Kontaktnaya zadacha teorii uprugosti [The Contact Problem of the Theory of Elasticity] / I. Ya. Shtaerman. – M.: Gostechteorizdat, 1949. – 272 p. [in Russian]
2. Kudishin YU. I. Metallicheskiye konstruktsii [Metal constructions] / YU. I. Kudishin, Ye. I. Belenya. – 13nd edition. – M.: Akademiya, 2011. – 688 p. [in Russian]
3. Sukharev I. P. Prochnost' sharnirnykh uzlov mashin [Strength of the hinge units of machines] / I. P. Sukharev. - M .: Mashinostroyeniye, 1977. – 168 p. [in Russian]
4. Panovko Y.A. G. Prochnost', ustoychivost', kolebaniya [Strength, stability, vibrations]. V 3 t. T.2. / YA. G. Panovko, I. A. Birger. – M.: Mashinostroyeniye, 1968. – 383-393 p. [in Russian]
5. Aleksandrov V. M. Kontaktnyye zadachi v mashinostroyenii [Contact tasks in engineering] / V. M. Aleksandrov, B. L. Romalis. - М.: Mashinostroyeniye, 1986. - 29-31 p. [in Russian]
6. Aleksandrov V. M. Kontaktnyye zadachi dlya tel s tonkimi pokrytiyami i prosloykami [Contact problems for bodies with thin coatings and interlayers] / V. M. Aleksandrov, S. M. Mkhitaryan. – M.: Nauka, 1983. – 488 p. [in Russian]
7. Popov G. Ya. Kontsentratsiya uprugikh napryazheniy vozle shtampov, raz-rezov tonkikh vklyucheniy i podkrepleniy [Concentration of elastic stresses near stamps, incisions of thin inclusions and reinforcements] / G. Ya. Popov. – M.: Nauka, 1982. – 344 p. [in Russian]
8. Teply M. I. Kontaktnyye zadachi dlya oblastey s krugovymi granitsami [Contact problems for domains with circular boundaries] / M. I. Teply. - Lviv: Vishcha shchola, 1983. – 176 p. [in Russian]
9. Bethune J.D. Engineering Design and Graphics with SolidWorks 2016 – Peachpit Press, 2016. — 784 p.
10. Planchard D. Official Certified SolidWorks Professional (CSWP) Certi-fication Guide with Video Instruction: SolidWorks 2012-2014 - SDC Publications, 2014. – 192 p.