ОБ АНАЛОГЕ ПОСТОЯННОЙ ЭЙЛЕРА-МАСКЕРОНИ И ЗАКОНОМЕРНОСТЯХ ЕГО ИЗМЕНЕНИЯ

Гербер А.Д.¹, Гербер Е.А.²

¹Кандидат физико-математических наук,

Тюменское высшее военно-инженерное командное училище имени маршала инженерных войск А.И.Прошлякова;

²Кандидат физико-математических наук,

ОАО Тьюбоскан

ОБ АНАЛОГЕ ПОСТОЯННОЙ ЭЙЛЕРА-МАСКЕРОНИ И ЗАКОНОМЕРНОСТЯХ ЕГО ИЗМЕНЕНИЯ

Аннотация

Работа посвящена описанию закономерностей аппроксимации частичной суммы обобщенного гармонического числового ряда. Ряды этого типа достаточно часто используются в теории чисел, в описании физических закономерностей и в вычислительной математике. В работе предложен вариант аналитической оценки частичной суммы обобщенного гармонического ряда форме Эйлера. То есть, частичная сумма равна значению интеграла от общего члена ряда для последнего учтенного слагаемого, плюс постоянная, плюс бесконечно-малая функция.  

Ключевые слова: Обобщенный гармонический ряд, постоянная Эйлера-Маскерони, гармонические числа, обобщенные гармонические числа, аналог постоянной Эйлера.

Gerber A.D¹, Gerber E.A.²

¹PhD in Physics and Mathematics,

Tyumen Higher Military Engineering Command School named after Marshal A.I. Proshlyakov;

²PhD in Physics and Mathematics,

OJSC Tuboskan

ON ANALOGUE OF EILER-MASKERONI CONSTANT AND REGULARITIES OF ITS CHANGE

Abstract

The paper is devoted to the description of approximation regularities of the partial sum of the generalized harmonic number series. Series of this type are often used in number theory, in the description of physical laws and computational mathematics. An option of the analytical estimation of the partial sum of the generalized harmonic series in the Eulerian form is proposed. That is, the partial sum is equal to the value of the general term integral of the series for the last counted term, plus a constant, plus an infinitesimal function.

Keywords: Generalized harmonic series, Euler-Mascheroni constant, harmonic numbers, generalized harmonic numbers, an analog of the Euler constant.

Наличие условной сходимости числового знакопеременного ряда, построенного на основе обобщенного гармонического ряда, определяет свойство, связанное с зависимостью его суммы от порядка суммирования. При вычислении предела частичной суммы такого ряда, состоящего из положительных и отрицательных слагаемых, возникает необходимость в использовании аналитической оценки отрезков расходящегося ряда [1, С. 33], [2, С. 17], [3, С. 319]. Актуальность поставленной задачи определяется так же тем, что ряды именно этого типа широко используются в различных областях математики и физики [4, С. 4], [5, С. 303].

В работе будет построена аналитическая оценка для частичных сумм обобщенного гармонического ряда:

  (1)

Ряд (1) при s>1 принято называть дзета-функцией Римана. Настольной книгой для изучения свойств этой функции можно считать монографию Титчмарша Е. [6, С. 9], изданную еще в 1959 году. Известно, что при s=1, частичная сумма для (1) называется гармоническим числом. Его аналитическую оценку обычно, следуя Эйлеру, записывают в следующей форме [3, С. 319], [5, С. 303], [7, С. 4]:

   (2)

где H_n – гармоническое число,  – постоянная Эйлера-Маскерони, a(n) – бесконечно малая функция. Отметим, что бесконечно малая функция, например, согласно [7, С. 4], имеет вид:

    (3)

Переписав формулу (2) по-другому, из сравнения площадей криволинейной трапеции и ступенчатой фигуры, оценим эту разность как сумму треугольников с основанием в единицу и высотой, равной разности значений функции в целочисленных точках, то есть, справедлива запись:

   (4)

Первое слагаемое в (4) получается близким по значению к постоянной Эйлера-Маскерони, а второе повторяет, основное по порядку малости, слагаемое остатка из [7, С. 4].  При рассмотрении обобщенного гармонического ряда (1) с показателем степени s<1 используется понятие обобщенного гармонического числа H_ns, которое, следуя Грэхему Р. [5, С. 308], будем называть гармоническим числом s-го порядка. Предположим, далее, что разность между гармоническим числом s-го порядка и выражением для интеграла от общего члена ряда будет также стремиться к постоянной, похожей на постоянную Эйлера-Маскерони, то есть справедлива запись:

   (5)

где  – аналог постоянной Эйлера-Маскерони, зависящий от значения показателя степени знаменателя ,  - бесконечно малая величина.

Анализ структуры остатка в той же форме, что и выше (4), дает оценку этой разности в следующем виде:

   (6)

То есть, для любых показателей степени знаменателя не равных единице, возможно существование постоянной, по структуре схожей с постоянной Эйлера-Маскерони, при этом главная часть бесконечно малой величины начинается со слагаемого, равному последнему учтенному слагаемому с коэффициентом примерно равным 0,5.

Анализ работ на тему обобщенных гармонических рядов, и свойств дзета-функции [5, С. 308], [6, С. 19], [8, С. 986], [9, С. 40], [10] показал, что оценка величины обобщенного гармонического числа в виде формулы (5) ранее не использовалось. Поскольку, такое представление гармонического числа s-го порядка оказалось неизвестным, то, для получения его абсолютных значений была проведена серия численных экспериментов, что для данного типа задач является скорее обычным делом. Например, работа Ю. Матиясевича [8, С. 990] посвящена компьютерным экспериментам по вычислению нулей дзета-функции с заданной точностью на основе использования конечных отрезков ряда Дирихле. В работах Luo Q. [9, С. 40] и Van Makderen R. [10] рассматриваются методы оценки частичных сумм обобщенного гармонического ряда с заданной точностью на основе рекуррентных и интегральных соотношений.

В нашем случае, для определения абсолютной величины аналога постоянной Эйлера  и коэффициентов бесконечно малой функции использовался метод наименьших квадратов. Для этого, для разного набора учтенных слагаемых n_i вычислялась величина:

   (7)

Вычисленные для возрастающего последовательности учтенных слагаемых  значения  использовались для определения коэффициентов представления остатка в следующей форме:

   (8)

где m – число слагаемых в представлении бесконечно малой. В результате, был получен массив значений аналога постоянной Эйлера, и первого коэффициента в (8) в зависимости от показателя степени знаменателя в интервале значений .

На следующем шаге, была предпринята попытка описания полученного массива значений аналога постоянной Эйлера на основе единого аналитического выражения. Для определения асимптотического характера поведения аналога постоянной Эйлера воспользуемся тем, что для случая, когда существует дзета-функция, то есть  s>1, слагаемое  в (5) будет стремиться к нулю, и справедливо тождество:

  (9)

Поэтому в качестве варианта аппроксимации массива данных по аналогу постоянной Эйлера был использована асимптотика следующего вида:

   (10)

Где, для значений показателя степени знаменателя в интервале  использование полинома 4-го порядка гарантировало точность определения величины аналога постоянной Эйлера в среднем до сотых долей процента. Конкретный вид полинома, обеспечивающего данную точность, представлен ниже в (11):

  (11)

Кроме того, оказалось, что коэффициент при первом слагаемом бесконечно малой добавки в виде (8), по крайней мере до показателей степени знаменателя менее 6, оказался равным примерно 0.5, то есть величине, полученной на основе грубой оценки из сравнения площадей фигур под кривой и ступенчатой фигуры, соответствующей частичной сумме ряда. Адекватность выражения (11), используемого для вычисления значения аналога постоянной Эйлера можно проверить на основе сравнения значений, вычисленных по ней и по формуле (9), которая связывает значения дзета-функции с этой постоянной. В предположении правильности формулы для аналога постоянной Эйлера (9) эта величина сравнивалась величиной, найденной по формуле (11), полученной на основе МНК обработки результатов численного эксперимента. Данные для четных значений дзета-функции были взяты из работ [4, С. 2]. Все рассчитанные величины значения аналога постоянной Эйлера по (9) и (11) представлены в таблице 1.

 

Таблица 1 – Оценка точности аппроксимации аналога постоянной Эйлера на основе формулы (11)

 

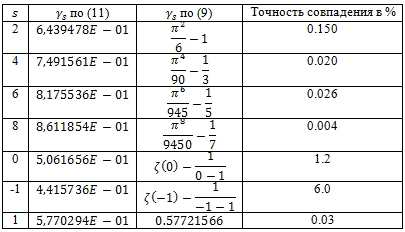
Существование значения дзета-функции для нулевых и отрицательных показателей степени базируется на том, что дзета-функция является решением функционального уравнения [4, С. 3], откуда следует, что ей, например, можно приписать значения и для тех показателей степени знаменателя, при которых соответствующий числовой является расходящимся, например,  .

Анализ результатов аппроксимации (см. табл. 1) для значений аналога постоянной Эйлера показывает, что имеется хорошее совпадение с ожидаемыми значениями по точности, не хуже точности, полученной в результате обработки данных численного эксперимента.

К основным результатам работы можно отнести доказательство справедливости существования аналога постоянной Эйлера, по крайней мере на уровне результатов численного эксперимента, и получении ее конкретной зависимости от показателя степени знаменателя, например, в виде (11), а использование представления частичной суммы на основе формулы (5) позволяет аналитически оценить частичные суммы обобщенного гармонического ряда для любых показателей степени знаменателя.

Список литературы / References

1. Уиттекер Э.Т., Курс современного анализа. Часть первая. Основные операции анализа. Издание второе / Э.Т. Уиттекер., Дж. Н. Ватсон – М.: Государственное издательство физико-математической литературы. 1963 – 343 с.
2. Гурса Э. Курс математического анализа. Том первый, часть вторая. Разложение в ряды, геометрические приложения / Э. Гурса. – Москва-Ленинград: Государственное технико-теоретическое издательство. 1933 – 235 с.
3. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. В 3 т., т. 2 / Г.М. Фихтенгольц. – М.: Физматлит. 2001. – 800 с.
4. Шишанин A.O. Дзета-функция Римана, ее знакопеременная версия и их q-аналоги / А.О. Шишанин // Инженерный журнал: наука и инновации. – 2013. – № 8. – С. 1-10.
5. Грэхем Р., Кнут Д., Паташник О. Конкретная математика. Основания информатики: Пер. с англ. / Р. Грэхем, Д. Кнут. – М.: Мир. 1998. – 706 с.
6. Титчмарш Е. К. Теория дзета-функции Римана / Е.К. Титчмарш. – Москва: ИЛ, 1953. – 408 с.
7. Anda Andrew A., Harmonic Sum Calculation: Sneaking Finite Precision Principles into CS1// Proceedings. Midwest Instruction and Computing Symposium. University of Minnesota, Morris. April 16 and 17, 2004. URL: http://www.micsymposium.org/mics_2004/proceedings.html
8. Matiyasevich Yu. V., Riemann's zeta function and finite Dirichlet series, Algebra i Analiz, 27:6 (2015), 174–198; St. Petersburg Math. J., 27:6 (2016), 985–1002
9. Luo Q., Wang Z., Numerical calculation of the Riemann zeta function at odd-integer arguments: a direct formula method. Mathematical Sciences March 2015, Volume 9, Issue 1, 39-45
10. Van Makderen Renaat, Riemann's Zeta Function. Numerical Evaluation via its Alternating Relative η(s). arXiv:1109.6790v2 [math.NT]. last revised 7 Oct 2011 (this version, v2)

Список литературы на английском языке / References in English

1. Whittaker E.T., Kurs sovremennogo analiza. Chast' pervaja. Osnovnye operacii analiza. Izdanie vtoroe [Course of modern analysis. Part one. Basic analysis operations. Second edition] / E.T. Whittaker, Vatson Dzh. N. – M.: Gosudarstvennoe izdatel'stvo fiziko-matematicheskoj literatury. 1963 – 343 p. [In Russian]
2. Gursa E., Kurs matematicheskogo analiza. Tom pervyj, chast' vtoraja. Razlozhenie v rjady, geometricheskie prilozhenija [Course of mathematical analysis. Volume one, part two. Expansion in series, geometric applications] / E. Gursa – Moskva-Leningrad: Gosudarstvennoe tehniko-teoreticheskoe izdatel'stvo. 1933 – 235 p. [In Russian]
3. Fikhtengolts G.M, Kurs differencial'nogo i integral'nogo ischislenija. V 3 t., t. 2 [Course of differential and integral calculus (in 3 volumes), v. 2] / G.M. Fikhtengolts. – M.: Fizmatlit. 2001. – 800 p. [In Russian]
4. Shishanin A.O., Dzeta-funkcija Rimana, ee znakoperemennaja versija i ih q-analogi [The Riemann zeta-function, its alternating version and their q-counterparts] / A.O. Shishanin // Inzhenernyj zhurnal: nauka i innovacii. – 2013. – № 8. – P. 1-10. [In Russian]
5. Graham R., Patashnik O. Konkretnaja matematika. Osnovanija informatiki: Per. s angl. [Specific mathematics. Foundations of Informatics: translation from English] / R. Grjehem, D. Knut. – M.: Mir. 1998. – 706 p. [In Russian]
6. Titchmarsh E. K. Teorija dzeta-funkcii Rimana [The theory of the Riemann zeta function] / E.K. Titchmarsh. – Moskva: IL, 1953. – 408 p. [In Russian]
7. Anda Andrew A. Harmonic Sum Calculation: Sneaking Finite Precision Principles into CS1// Proceedings. Midwest Instruction and Computing Symposium. University of Minnesota, Morris. April 16 and 17, 2004. URL: http://www.micsymposium.org/mics_2004/proceedings.html
8. Matiyasevich Yu. V. Riemann's zeta function and finite Dirichlet series, Algebra i Analiz, 27:6 (2015), 174–198; St. Petersburg Math. J., 27:6 (2016), 985–1002
9. Luo Q., Wang Z. Numerical calculation of the Riemann zeta function at odd-integer arguments: a direct formula method. Mathematical Sciences March 2015, Volume 9, Issue 1, 39-45
10. Van Makderen Renaat. Riemann's Zeta Function. Numerical Evaluation via its Alternating Relative η(s). arXiv:1109.6790v2 [math.NT]. last revised 7 Oct 2011 (this version, v2)