НЕКОТОРЫЕ ДОПОЛНЕНИЯ К ВОПРОСАМ О МНОГОМЕРНЫХ ИНТЕГРАЛЬНЫХ ОПЕРАТОРАХ С ОСЦИЛЛИРУЮЩИМИ КОЭФФИЦИЕНТАМИ

Волосатова Т.А.¹, Данекянц А.Г.²

¹ORCID: 0000-0001-6416-0212, Кандидат физ.-мат. наук,

Донской государственный технический университет (Ростов-на-Дону)

²ORCID: 0000-0002-0409-0694, Кандидат физ.-мат. наук,

Донской государственный технический университет (Ростов-на-Дону)

НЕКОТОРЫЕ ДОПОЛНЕНИЯ К ВОПРОСАМ О МНОГОМЕРНЫХ ИНТЕГРАЛЬНЫХ ОПЕРАТОРАХ С ОСЦИЛЛИРУЮЩИМИ КОЭФФИЦИЕНТАМИ

Аннотация

В статье представлены многомерные интегральные операторы с однородными ядрами и радиальными осциллирующими коэффициентами вида |x|^iδ, действующие в пространстве L₂(B_n). Для операторов такого вида определен символ, в терминологии которого получены необходимые и достаточные условия нётеровости и вычислительная формула для индекса. Так же сформулирован критерий нётеровости и формула индекса для близкого класса операторов, действующих в L₂(B_n). В данной статье, приведены некоторые важные дополнения и уточнения к основным результатам , опубликованным ранее, и в качестве дополнения рассмотрен частный случай интегрального оператора.

Ключевые слова: интегральные операторы с однородными ядрами, интегральные операторы с осциллирующимикоэффициентами, критерий нётеровости, многомерные интегральные уравнения.

Volosatova T.A.¹, Danekiants A.G.²

¹ORCID: 0000-0001-6416-0212, PhD in Physics and Mathematics,

Don State Technical University (Rostov-on-Don)

²ORCID: 0000-0002-0409-0694, PhD in Physics and Mathematics,

Don State Technical University (Rostov-on-Don)

SOME ADDITIONS TO THE PROBLEM OF MULTIDIMENSIONAL INTEGRAL OPERATORS WITH OSCILLATING COEFFICIENTS

Abstract

The paper presents multidimensional integral operators with homogeneous cores and radial oscillating coefficients of |x|^iδ, acting in space L₂(B_n). A symbol is defined for operators of this type in the terminology while necessary and sufficient conditions for noethericity and the computational formula for the index are obtained. A criterion for noethericity property and the index formula for a similar class of operators acting in L₂(B_n) have been established. In this paper, we give some important additions and refinements to the main results published earlier. We have also considered a special case of an integral operator as a supplement.

Keywords: integral operators with homogeneous cores, integral operators with oscillating coefficients, criterion for noethericity, multidimensional integral equations.

В современном мире уровень развития страны во многом определяется уровнем развития и эффективностью инновационной деятельности. Инновационная деятельность компаний различных секторов экономики основывается на научно-технических разработках и их реализации. На начальном этапе работы проекта необходимо построение модели процесса, ее исследование, и нахождение оптимальных путей решения поставленной задачи. При решении прикладных задач зачастую возникают сложные математические модели. Для проведения таких научных исследований, зачастую, требуются глубокие и специфические знания. Поэтому с развитием и усложнением технических задач должен разрастаться и совершенствоваться математический аппарат. Так интегральные уравнения и теория интегральных операторов, имеют широкое применение во многих областях науки: в физике, в строительстве, в теплоэнергетике, в биологии и медицине. Теория интегральных операторов с однородными ядрами в современной математики достаточно изучена. Но зачастую возникает необходимость строить и исследовать новые алгебры и для них строить символические исчисления. Данная статья посвящена многомерным интегральным оператором с однородными ядрами и специфическими коэффициентами вида |x|^iδ, действующим в пространстве L₂(B_n).

Напомним некоторые общие обозначения, принятые в работах [1, С. 149],[2, C. 124], [3, C. 360] и которые, мы будем использовать в дальнейшем: − n-мерное евклидово пространство точек  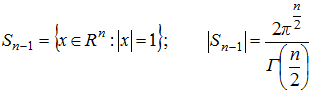-площадь сферы  − компактификация пространства R одной бесконечно удаленной точкой;  − преобразование Фурье функции, .

Внесем некоторые дополнения в схему рассуждений, приведенных, в [1, С. 149],[2, C. 124], [3, C. 361]. Сформулируем постановку задачи. В пространстве L₂(B_n) проанализируем оператор

     (1)

где , а функция  удовлетворяет надлежащим условиям:

1) однородность степени (-n), то есть ;

2) инвариантность относительно группы вращений , то есть

;

3) суммируемость, то есть .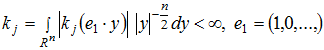

В L₂(B_n) представлен интегральный оператор с ядром, удовлетворяющим условию (1):

,               (2)

Оператору A поставим в соответствии оператор 

,               (3)

где - оператор вида (2) с ядром . В работах [2, C. 124],[3, C. 360], было доказано, что оператор A нетёров ⇔ оператор  нетёров, причем .

Далее, осуществим переход к интегральному уравнению. Обратимся вновь к оператору A. В пространстве L₂(B_n) подвергнем рассмотрению уравнение, порожденное оператором A:

.     (4)

Существование функций , таких что , обосновывается тем фактом, что функции  удовлетворяют условию (2). Используя это, и переходя в уравнении (4) к сферическим координатам , получаем:

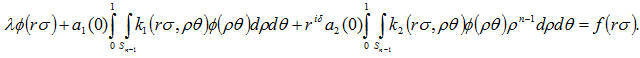
Опираясь на однородность функции , имеем:

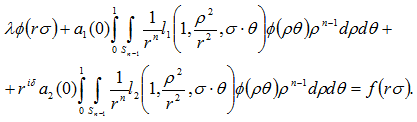
Умножая правую и левую часть равенства на , получим следующее выражение:

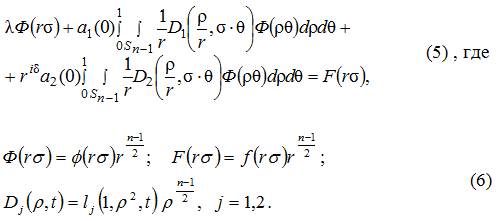
Отметим, что функция  удовлетворяет условию суммируемости

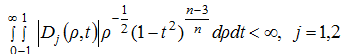.                (7)

Действительно, применяя формулу (6), далее, применяя к интегралу по отрезку формулу Каталана, имеем:

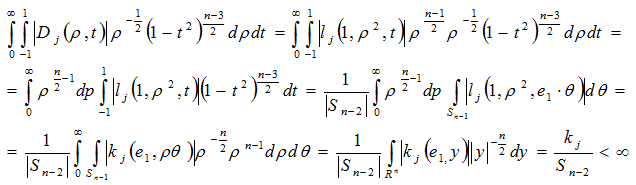
С помощью увеличения обеих частей выражения на сферические гармоники , интегрирования по сфере единичного радиуса, и с помощью формулы Функа-Гекке, получим следующую бесконечную диагональную систему одномерных интегральных уравнений:

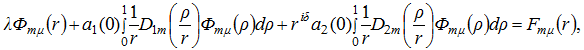    (8)

где  − размерность пространства сферических гармоник порядка m.

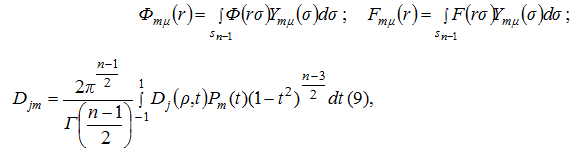
при этом  - многочлены Лежандра.

Покажем связь многомерного оператора с одномерным. В пространстве  оператор , формирует левую часть уравнения (8)

.

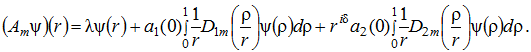Чтобы получить критерий нётеровости оператора , в работах [2, C.124]; [3, C. 361], был приведен переход к интегральным операторам с разностными ядрами. С этой целью был определен изоморфизм  формулой

.

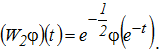В  оператор , определялся формулой

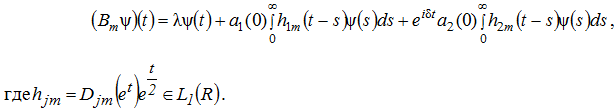
Символом оператора назвали функцию .

Подвергнем функцию  преобразованию, а именно:

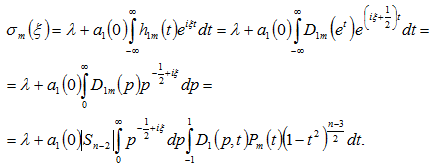
Применяя к интегралу по отрезку формулу Каталана, получили:

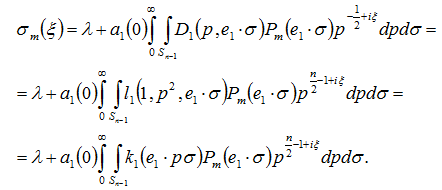
Окончательно, имеем: .        (9)

В [3, C. 360] доказано, что оператор  нётеров , при этом .

Рассмотрим частный случай оператора A, а именно, введем оператор   где K определяется формулой (2).

Следствие. Оператор C нётеров в пространстве L₂(B_n) в том и только в том случае, когда  . В этом случае .

Доказательство. Заметим, что в этом случае . Применяя теорему, получаем, что нётеровость оператора C равносильна условию . Далее, так как .

Таким образом, дополнительные исследования, представленные в данной статье, позволили вывести критерий нётеровости и получить развернутые формулы для индекса в случае частного вида интегрального оператора. Такая развитая теория позволяет применять полученные результаты при решении прикладных задач, которые могут возникать в различных областях экономики, физики, биологии, химии. Следует отметить, что операторы с однородными ядрами и радикальными (по меньшей мере, в окрестности точки x=0) коэффициентами используются одним из авторов при решении некоторых практических задач теплоэнергетики, которые приводят к задачам математической физики [4, C.146], [5, C.134],[6, C. 68].

 

Список литературы / References

1. Данекянц А.Г. К вопросам построения интегральных операторов с осциллирующими коэффициентами в пространстве L2(BN) / А.Г. Данекянц // Инженерный вестник Дона. – 2013. – Т. 27. – № 4. – С. 149.
2. Данекянц А.Г. Интегральные операторы с однородными ядрами и осциллирующими коэффициентами / А.Г. Данекянц // Интернет-журнал Науковедение. – 2013. – № 5 (18). – С. 124.
3. Данекянц А.Г. Связь многомерного интегрального оператора с осциллирующими коэффициентами с одномерными операторами в L2(BN) / А.Г. Данекянц // Научное обозрение. – 2014. – № 10-2. – С. 360-362.
4. Волосатова Т.А. Некоторые вопросы энергоэффективности тепловых сетей в разрезе текущего состояния комплекса ЖКХ России / Т.А. Волосатова // Инженерный вестник Дона. – 2013. – Т. 27. – № 4. – С. 146.
5. Волосатова Т.А. Основные вопросы энергоэффективности тепловых водяных котельных и варианты их решения / Т.А. Волосатова // Инженерный вестник Дона. – 2013. – Т. 26. – № 3 (26). – С. 134.
6. Волосатова Т.А. Современные способы повышения энергетической эффективности жилых зданий / Т.А. Волосатова // Инженерный вестник Дона. – 2015. – Т. 36. – № 2-2. – С. 68.

Список литературы на английском языке / References in English

1. Danekjanc A.G. K voprosam postroenija integral'nyh operatorov s oscillirujushhimi kojefficientami v prostranstve L2(BN) [To problems of construction of integral operators with oscillating factors in space L2 (BN)] / A.G. Danekjanc // Inzhenernyj vestnik Dona. [Engineering journal of Don] – 2013. – V. 27. – № 4. – P. 149. [in Russian]
2. Danekjanc A.G. Integral'nye operatory s odnorodnymi jadrami i oscillirujushhimi kojefficientami [Integral operators with homogeneous kernels and oscillating factors] / A.G. Danekjanc // Internet-zhurnal Naukovedenie. [Scientific open access journal «Naukovedenie»] – 2013. – № 5 (18). – P. 124. [in Russian]
3. Danekjanc A.G. Svjaz' mnogomernogo integral'nogo operatora s oscillirujushhimi kojefficientami s odnomernymi operatorami v L2(BN) [Connection of a many-dimensional integral operator with oscillating factors with one-dimensional operators in L2 (BN)] / A.G. Danekjanc // Nauchnoe obozrenie. [Science-review]. – 2014. – № 10-2. – P. 360-362. [in Russian]
4. Volosatova T.A. Nekotorye voprosy jenergojeffektivnosti teplovyh setej v razreze tekushhego sostojanija kompleksa ZhKH Rossii [Some problems of power efficiency of thermal webs in a slit of a current condition of a complex of housing and communal services of Russia] / T.A. Volosatova // Inzhenernyj vestnik Dona. [Engineering journal of Don]. – 2013. – V. 27. – № 4. – P. 146. [in Russian]
5. Volosatova T.A. Osnovnye voprosy jenergojeffektivnosti teplovyh vodjanyh kotel'nyh i varianty ih reshenija [The basic problems of power efficiency of thermal water boiler-houses and variants of their solution] / T.A. Volosatova // Inzhenernyj vestnik Dona. [Engineering journal of Don]. – 2013. – V. 26. – № 3 (26). – P. 134. [in Russian]
6. Volosatova T.A. Sovremennye sposoby povyshenija jenergeticheskoj jeffektivnosti zhilyh zdanij [Modern modes of a raise of power efficiency of residential buildings] / T.A. Volosatova // Inzhenernyj vestnik Dona. [Engineering journal of Don]. – 2015. – V. 36. – № 2-2. – P. 68. [in Russian]