ИСПОЛЬЗОВАНИЕ ПРОГРАММЫ GEOGEBRA ДЛЯ ВИЗУАЛИЗАЦИИ СВОЙСТВ КРИВЫХ ВТОРОГО ПОРЯДКА

Ушаков А.В.

ORCID: 0000-0002-7665-2086, Кандидат физико-математических наук, Доцент, Московский Городской Педагогический Университет

ИСПОЛЬЗОВАНИЕ ПРОГРАММЫ GEOGEBRA ДЛЯ ВИЗУАЛИЗАЦИИ СВОЙСТВ КРИВЫХ ВТОРОГО ПОРЯДКА

Аннотация

Данная статья посвящена некоторым аспектам преподавания курса аналитической геометрии в педагогическом университете. Здесь исследованы возможности компьютерной программы geogebra для визуализации свойств кривых второго порядка на примере эллипса. В результате создано электронное пособие, которое можно использовать как презентацию на лекции, или как материал для практического занятия в компьютерном классе. Изложение построено в форме заданий для студентов, предполагающих обобщение и систематизацию изученных фактов.

Ключевые слова: кривые второго порядка, программа geogebra, обучение студентов.

Ushakov A.V.

ORCID: 00000000-0002-7665-2086, PhD in Physics and Mathematics, Associate Professor, Moscow City Pedagogical University

USE OF GEOGEBRA PROGRAM FOR VISUALIZING PROPERTIES OF SECOND ORDER CURVES

Abstract

This article deals with some aspects of analytic geometry teaching at pedagogical universities. It discusses the potential of geogebra computer program for visualizing the properties of second-order curves on the example of an ellipse. As a result, an electronic manual has been created that can be used for presentations at a lecture, or as material for a practical lesson at a computer class. The presentation is constructed in the form of assignments for students, suggesting the generalization and systematization of the studied facts.

Keywords: second order curves, geogebra program, training of students.

Одним из приоритетных направлений развития образования сегодня является его информатизация. Так, в процессе обучения математике использование компьютерных технологий призвано способствовать формированию основных понятий, организации работы с теоретическим и практическим материалом, приобретению необходимых умений и навыков, служить средством контроля и самоконтроля.

На примере эллипса, гиперболы и параболы студенты учатся выводить уравнения кривых линий по их определениям, после чего исследовать свойства кривых по их уравнениям. При этом часто возникает необходимость визуализировать результаты сложных алгебраических выкладок с помощью интерактивных электронных чертежей. Для изображения геометрических конструкций существуют различные компьютерные средства. В данной статье используется программа geogebra, которая представляет собой динамическое программное обеспечение всего курса высшей математики. Эта программа распространяется бесплатно, имеет интуитивно понятный интерфейс и является по-настоящему мобильной, поскольку работает как на стационарном компьютере или ноутбуке, так и на планшете или смартфоне. После запуска geogebra появляется следующее окно: (рис. 1):

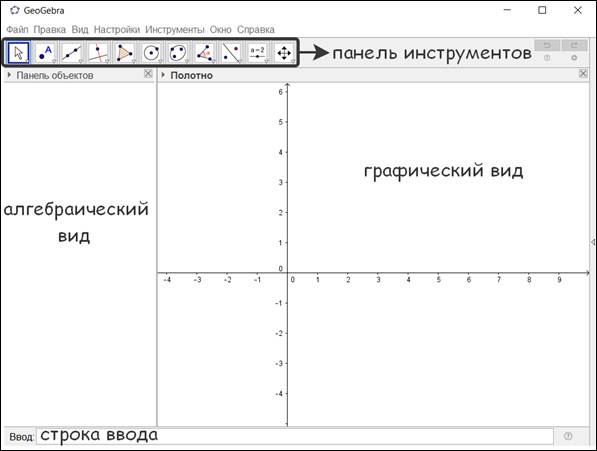
Рис. 1 – стартовое окно программы geogebra.

Интерактивная геометрия программы geogebra позволяет строить фигуры в поле графического вида с помощью электронных аналогов различных чертежных инструментов на соответствующей панели. Аналитическая запись этих построений отображается в поле алгебраического вида. С другой стороны, координаты и уравнения можно задавать непосредственно в строке ввода, применяя специальные команды для выполнения сложных математических вычислений. Таким образом, на каждом чертеже тесно взаимодействуют алгебра и геометрия.

Перейдем теперь к описанию заданий по изучению свойств эллипса в программе geogebra.

Задание 1. Постройте эллипс, руководствуясь его определением.

Эллипсом называется множество γ всех точек плоскости, для каждой из которых сумма расстояний до двух фиксированных точек F₁ и F₂ (называемых фокусами эллипса) является постоянной величиной, большей расстояния между фокусами.

Обозначим расстояние между фокусами через 2с, а сумму расстояний от точек эллипса до фокусов через 2а. Будем считать, что фокусы лежат на оси абсцисс, симметрично относительно начала координат. Начертим сначала окружность с центром F₁ радиуса R, а затем вторую окружность с центром F₂ радиуса 2а–R. Если a–c≤R≤a+c, то эти окружности пересекаются в точках, принадлежащих эллипсу.

Список построений для задания 1.

1. Создайте ползунок для изменения расстояния межу фокусами. Щелкните инструментом ползунок на графическом поле и в появившемся окне укажите имя ползунка с, минимальное значения 0, максимальное значение 15.
2. Постройте фокусы F₁(–с, 0) и F₂(с, 0), напечатав в строке ввода последовательно F_1=(-с, 0) и F_2=(c, 0).
3. Создайте надпись F_1,2(±с, 0) – фокусы. Щелчок инструментом текст на графическом поле вызывает окно, где можно набрать комментарий в разделе правка. Список LaTeX-формула содержит шаблоны для корректной записи различных математических выражений.
4. Создайте еще два ползунка, которые позволят изменять значения параметра a от с до 15 и радиуса R от а–с до а+с.
5. Постройте окружности с центрами в точках F₁ и F₂, радиусов R и 2а–R. Щелкните инструментом окружность по центру и радиусу соответствующий фокус, после чего появится окно для ввода радиуса. Имена, присвоенные окружностям по умолчанию, измените на α и β из контекстного меню. Для ввода греческих букв нажмите кнопку α.
6. Постройте точки А и В пересечения окружностей α и β, щелкнув инструментом пересечение по каждой из них. Ясно, что сумма расстояний от любой из этих точек до фокусов будет равна 2а. Из контекстного меню включите след для точек А и В, а также скройте их имена.
7. Двигая ползунок R инструментом перемещение, постройте множество точек эллипса как след точек А и В. Команда Вид→Обновить (Ctrl+F) стирает построенный след.
8. Создайте флажок задание 1 скрывающий или показывающий построенные фигуры. Щелчок инструментом флажок на графическом поле вызывает окно, в котором надо указать название флажка и выбрать окружности α и β из списка объектов.

Задание 2. Постройте эллипс по его каноническому уравнению.

Выведем уравнение эллипса. Для произвольной точки М(x, y) находим  и

Если M∈γ, то r₁+r₂=2a, откуда r₁=2a–r₂ или в координатной форме . Возведем обе части этого равенства в квадрат

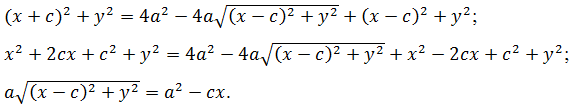
Ещё раз возведем в квадрат

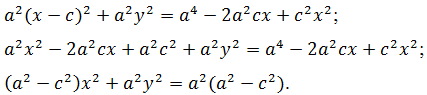
Обозначив , получим уравнение , которое после сокращения на  принимает вид  и называется каноническим уравнением эллипса.

Обратно, если координаты точки М удовлетворяют этому уравнению, то  и

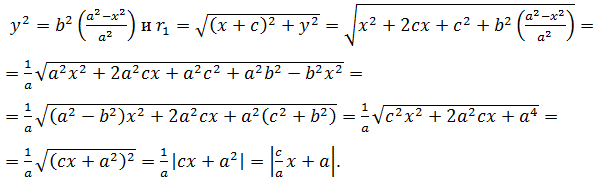
Поскольку a>c и |x|≤a, то . Аналогично, . Таким образом, r₁+r₂=2a, следовательно, M∈γ.

Список построений для задания 2.

1. Вычислите 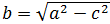, напечатав b=sqrt(a^2-c^2).
2. Создайте динамический текст 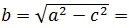 и выберете значение b из списка объектов.
3. Постройте эллипс 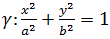, напечатав g:x^2/a^2+y^2/b^2=1.
4. Создайте надпись .
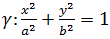5. Постройте вершины эллипса A₁(–a, 0), A₂(a, 0), B₁(0, –b), B₂(0, b).
6. Создайте надпись .
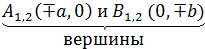7. Создайте флажок задание 2, который скрывает или показывает построенный эллипс, чтобы сравнить его с результатом задания 1.
8. Двигая ползунки a и c, проследите за изменением формы эллипса.

Задание 3. Постройте фокальные радиусы эллипса.

Фокальными радиусами точки M∈γ, называются отрезки MF₁ и MF₂ или их длины.

Список построений для задания 3.

1. Укажите точку M∈γ, щелкнув инструментом точка на эллипсе.
2. Постройте фокальные радиусы MF₁ и MF₂ точки M. Щелкните инструментом отрезок сначала точки M и F₁, а затем точки M и F₂. Из контекстного меню переименуйте построенные отрезки как r₁ и r₂. Программа автоматически рассчитает длины этих отрезков под аналогичными именами.
3. Вычислите r=r₁+r₂, напечатав r=r_1+r
4. Создайте динамический текст |MF₁|=r₁=, |MF₂|=r₂=, r₁+r₂= и выберете значения r₁, r₂, r из списка объектов.
5. Включите динамику точки M из контекстного меню. В левом нижнем углу графического поля появится значок, запускающий или останавливающий анимацию. Убедитесь, что при движении точки M по эллипсу изменяются числа r₁ и r₂, а их сумма имеет постоянное значение 2а.
6. Создайте флажок задание 3, скрывающий или показывающий построенные на этом этапе объекты.

Задание 4. Постройте директрисы эллипса.

Число  называется эксцентриситетом эллипса. Ясно, что 0<ε<1.

Прямые   называются директрисами эллипса, соответствующими фокусам F₁ и F₂. Для произвольной точки М(x, y) находим  

Если M∈γ, то, как мы видели,  следовательно, .

Обратно, если , то r₁=ερ₁ или в координатной форме . Учитывая, что  возведем обе части этого равенства в квадрат: ;

Таким образом, M∈γ.

Список построений для задания 4.

1. Вычислите эксцентриситет 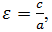 напечатав ε=c/a.
2. Постройте директрисы 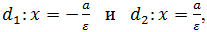 напечатав d_1:x=-a/ε и d_2:x=a/ε.
3. Через точку М проведите прямую, перпендикулярную директрисам. Щелкните инструментом перпендикулярная прямая сначала точку, а затем любую директрису.
4. Найдите точки C и D пересечения этого перпендикуляра с директрисами d₁ и d₂. Скройте перпендикуляр из контекстного меню.
5. Постройте отрезки MC и MD, переименуйте их как ρ₁ и ρ₂, после чего скройте имена точек C и D.
6. Вычислите значение 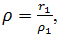, напечатав ρ=r_1/ρ_1
7. Создайте динамический текст 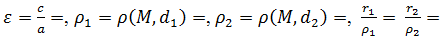 и выберете значения ε, ρ₁, ρ₂, ρ из списка объектов.
8. Перемещая ползунки a и c, установите связь между формой эллипса и эксцентриситетом.
9. Включив динамику точки М, убедитесь, что числа ρ₁ и ρ₂ изменяются, а частное 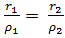 имеет постоянное значение ε.
10. Создайте флажок задание 4, скрывающий или показывающий построенные на этом этапе объекты.

Результатом этих заданий является следующий чертеж (рис. 2):

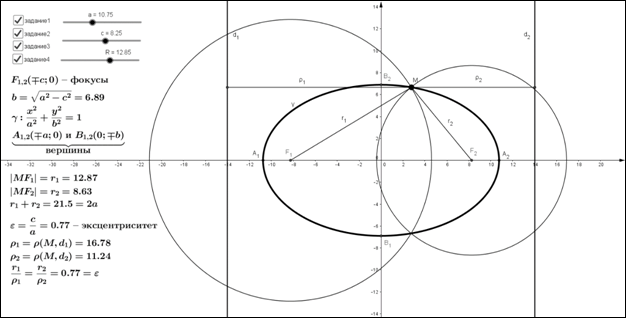
Рис. 2 – изучение свойств эллипса в программе geogebra.

Наличие на построенном чертеже интерактивных элементов и динамического текста, позволит студентам детально изучить свойства эллипса или самостоятельно установить некоторые закономерности. Кроме того, использование компьютерной графики положительно скажется на развитии воображения и интуиции студентов, их творческих способностей.

Список литературы / References

1. Кирюшкина О.В. Лабораторные работы как средство повышения эффективности формирования базовых понятий математического анализа у студентов педагогического профиля / О.В. Кирюшкина, М.В. Шуркова // Вестник Московского городского педагогического университета. Серия Информатика и информатизация образования – 2015. – №3(33). – С. 67-71
2. Ушаков А.В. О роли примеров на лекциях по топологии в педагогическом ВУЗе / А.В. Ушаков // Педагогические науки. – 2012. – № 3 (54). – С. 74-84.
3. Ушаков А.В. О роли примеров на лекциях по дифференциальной геометрии в педагогическом ВУЗе / А.В. Ушаков // Педагогические науки. – 2014. – № 3 (66). – С. 31-34.
4. Ушаков А.В. Использование информационных технологий при изучении геометрии в педагогическом ВУЗе / А.В. Ушаков // Педагогические науки. – 2015. – № 2 (71). – С. 55-57.
5. Педагогическая направленность математических дисциплин в подготовке будущих учителей математики: Монография / А.В. Ушаков, Ю.А. Семеняченко, В.Г. Покровский и др. – М.: Издательство «Спутник+», 2016. – 144 с.

Список литературы на английском языке / References in English

1. Kirjushkina O.V. Laboratornye raboty kak sredstvo povyshenija jeffektivnosti formirovanija bazovyh ponjatij matematicheskogo analiza u studentov pedagogicheskogo profilja [Laboratory work as a means of improving the efficiency of the formation of the basic concepts of mathematical analysis of the students ' pedagogical profile] / O.V. Kirjushkina, M.V. Shurkova // Vestnik Moskovskogo gorodskogo pedagogicheskogo universiteta. Serija Informatika i informatizacija obrazovanija [Bulletin of Moscow city Pedagogical University. Series of Informatics and Informatization of education] – 2015. – №3(33). – S. 67-71. [in Russian]
2. Ushakov A.V. O roli primerov na lekcijah po topologii v pedagogicheskom VUZe [On the role of examples in lectures on topology in Pedagogical University] / A.V. Ushakov // Pedagogicheskie nauki [Pedagogical sciences] – 2012. – № 3 (54). – P. 74-84. [in Russian]
3. Ushakov A.V. O roli primerov na lekcijah po differencial'noj geometrii v pedagogicheskom VUZe [On the role of examples in lectures on differential geometry in the Pedagogical University] / A.V. Ushakov // Pedagogicheskie nauki [Pedagogical sciences] – 2014. – № 3 (66). – P. 31-34. [in Russian]
4. Ushakov A.V. Ispol'zovanie informacionnyh tehnologij pri izuchenii geometrii v pedagogicheskom VUZe [The use of information technology in studying geometry at the Pedagogical University] / A.V. Ushakov // Pedagogicheskie nauki [Pedagogical sciences] – 2015. – № 2 (71). – P. 55-57. [in Russian]
5. Pedagogicheskaja napravlennost' matematicheskih disciplin v podgotovke budushhih uchitelej matematiki: Monografija [Pedagogical orientation of the mathematical sciences in preparation of future teachers of mathematics: Monograph] / A.V. Ushakov, Ju.A. Semenjachenko, V.G. Pokrovskij and others – M.: Izdatel'stvo «Sputnik+», 2016. – 144 p. [in Russian]