ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА ПРИ РАСЧЕТЕ РЕАКЦИИ СИНТЕЗА БЕНЗИЛИДЕНБЕНЗИЛАМИНА
Искандарова Д.Г.1, Карамова А.И.2
1Магистр; 2кандидат физико-математических наук, доцент,
ФГБОУ ВПО СФ «Башкирский государственный университет»
ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА ПРИ РАСЧЕТЕ РЕАКЦИИ СИНТЕЗА БЕНЗИЛИДЕНБЕНЗИЛАМИНА
Аннотация
В работе приводится постановка задачи планирования эксперимента, при расчете реальных процессов данная задача должна решаться на начальном этапе, предшествующем эксперименту. В данной работе предложен алгоритм поиска оптимального соотношения концентраций исходных веществ с целью получения максимального выхода продуктов реакции.
Ключевые слова: задача оптимизации, химическая кинетика, планирование эксперимента, начальные концентрации веществ, метод перебора.
Iskandarova D.G. 1, Karamova A.I. 2
1Master student; 2 candidate of physical and mathematical sciences, docent, Bashkir State University
PLANNING EXPERIMENT IN CALCULATING SYNTHESIS REACTION BENZYLIDENEBENZYLAMINE
Abstract
In this paper considers the problem of experiment planning, this problem must be addressed at an early stage, prior to experiment. An algorithm for finding the optimal ratio of the concentrations of the starting materials in order to obtain the maximum yield of the reaction products
Keywords: chemical kinetics, experiment planning, initial concentration of substances, search method.
Планирование эксперимента в химии, раздел материальной статистики, изучающий методы организации совокупности опытов с различными условиями для получения наиболее достоверной информации о свойствах исследуемого объекта при наличии неконтролируемых случайных возмущений. Величины, определяющие условия данного опыта, обычно называют факторами (например, температура, концентрация), их совокупность – факторным пространством. Набор значений факторов характеризует некоторую точку факторного пространства, а совокупность всех опытов составляет так называемый факторный эксперимент. Расположение точек в факторном пространстве определяет план эксперимента, который задает число и условия проведения опытов с регистрацией их результатов.
Механизм химической реакции можно представить в виде:
![]() (1)
(1)
где ![]() – вещества участвующие в реакции, n – количество веществ, m – количество реакций.
– вещества участвующие в реакции, n – количество веществ, m – количество реакций.
Часто на этапе теоретической оптимизации температуру рассматривают в качестве управления с заданным критерием эффективности в виде максимального или минимального выхода конкретных веществ. В общем виде задача оптимизации имеет вид:
![]() (2)
(2)
где ![]() – концентрации реагирующих веществ,
– концентрации реагирующих веществ, ![]() – вектор начальных концентраций веществ,
– вектор начальных концентраций веществ, ![]() – заданное множество допустимых значений начальных концентраций;
– заданное множество допустимых значений начальных концентраций; ![]() – промежуток времени функционирования системы [3].
– промежуток времени функционирования системы [3].
В реальном эксперименте в начальный момент времени между исходными веществами может присутствовать некоторая зависимость
![]() (3)
(3)
что позволяет сократить число степеней свободы в начальных данных.
На множестве U определен функционал качества управления
![]() (4)
(4)
Требуется найти такой вектор ![]() , что
, что
![]() (5)
(5)
Задача (2)-(5) называется задачей Майера [1].
Рассмотрим построение задачи оптимизации на синтезе бензилиденбензиламина реакцией бензиламина с четыреххлористым углеродом под действием FeCl3∙6H2O. механизм реакции задан в виде (6) с начальными условиями (7).
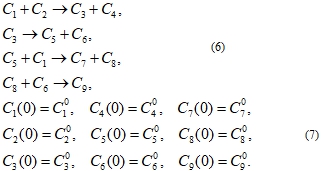
где C1=C7H9N – бензиламин, C2=CCl4– четыреххлористый углерод, C3=C7H8NCl – хлорбензиламин, C4=CHCl3 – хлороформ, C5=C7H7N – 1-фенилметанимин, C6=HCl – хлористый водород, C7=C14H13N – бензилиденбензиламин, C8=NH3 – аммиак, C9 =NH4Cl – хлористый аммоний.
Поскольку исходными являются вещества ![]() то начальные концентрации этих веществ связаны соотношением
то начальные концентрации этих веществ связаны соотношением
![]() .
.
Значения концентраций веществ ![]() можно менять с целью проведения реакции в сторону увеличения выхода продукта реакции, например
можно менять с целью проведения реакции в сторону увеличения выхода продукта реакции, например ![]() . Тогда критерий оптимальности имеет вид
. Тогда критерий оптимальности имеет вид
![]() . (8)
. (8)
По закону действующих масс скорости реакций определяются уравнениями:
![]() (9)
(9)
тогда кинетическая модель имеет вид
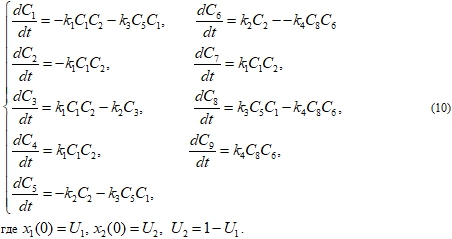
Данная задача может быть решена различными способами, рассмотрим ее решение на основе метода случайного поиска [2] или методе перебора (начальных концентраций исходных веществ). Для этого была разработана программа для решения обратной кинетической задачи методом случайного поиска максимизации функционала, работающая по следующему алгоритму:
- Задается механизм реакций.
- Задаются диапазон изменения начальных параметров и шаг для построения узлов.
- Формируется система дифференциальных уравнений и осуществляется ее решение методом Рунге-Кутта с различными начальными данными.
- Среди построенных решений идет поиск максимального значения концентрации целевого вещества в конечный момент времени. Как только максимум найден, оптимальное решение выгружается в файл.
В частности для данной реакции было получено, что оптимальным является следующее соотношение исходных веществ ![]() и при этом максимальный выход продукта составляет 99,6%.
и при этом максимальный выход продукта составляет 99,6%.
Литература
- Пантелеев А.В., Бортаковский А.С. Теория управления в примерах и задачах: учебное пособие. – М.: Высшая школа, 2003. – 583 с.
- Самойленко В.И., Пузырев В.А., Грубрин И.В. Техническая кибернетика: учебное пособие. – М.: Издательство МАИ, 1994. – 280 с.
- Степашина Е.В., Мустафина С.А. Графовый подход при моделировании каталитических процессов с переменным реакционным объемом // Системы управления и информационные технологии. 2012. Т.47. №1. С.14-19.
