ОБРАБОТКА ИМПУЛЬСНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ МЕТОДОМ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ

Пахотин В.А.¹, Рудниченко В.В.², Гюлумян Д.К.³

¹доцент физико-математических наук; ²магистрант; ³магистрант, Балтийский федеральный университет им. И. Канта

ОБРАБОТКА ИМПУЛЬСНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ МЕТОДОМ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ

Аннотация

Представлена методика обработки произвольной импульсной последовательности методом максимального правдоподобия. Получены выражения, определяющие алгоритмы оптимальной обработки импульсной последовательности  и выражения для дисперсии амплитуды и времени приема. Рассмотрен вопрос о разрешении двух импульсных последовательностей с различными амплитудами и временами приема. Дана оценка эффективности решения задачи разрешения двух импульсных последовательностей. Показано, что использование корреляционной функции позволяет устранить мешающее влияние боковых максимумов при обработке импульсной последовательности.

Ключевые слова: метод максимального правдоподобия, оптимальная обработка последовательности импульсов, разрешение импульсных последовательностей.

Pahotin V.A.¹, Rudnichenko V.V.², Gjulumjan D.K.³

¹associate professor; ²master student; ³master student, Immanuel Kant Baltic federal university

PROCESSING OF PULSE SEQUENCE BY THE METHOD OF  MAXIMUM LIKELIHOOD ESTIMATION

Abstract

A methodology of processing an arbitrary pulse sequence by the method of maximum likelihood estimation is presented. The expressions defining the optimum processing algorithms pulse sequence and expression for the variance of the amplitude and time of receipt are derived. The question of the resolution of two pulse sequences with different amplitudes and time of receipt is considered. The efficacy of the solution of the resolution of two pulse sequences is assessed. It is shown that the use of the correlation function eliminates interference from side peaks in the processing of the pulse sequence.

Keywords: maximum likelihood estimation, the optimum processing of pulse sequence, the resolution of pulse sequences.

Введение

Импульсные последовательности радиоимпульсов широко используются в различных комплексах аппаратуры. Основой их применения является возможность существенного увеличения энергии сигнала при сохранении ширины корреляционной функции. Это приводит к высокой помехоустойчивости и высокой разрешающей способности. Широко известны сигналы на основе кодов Баркера, сигналы с линейно меняющейся частотой (ЛЧМ-сигналы), сигналы на основе m-последовательностей. Они характеризуются малыми боковыми лепестками корреляционной функции, что определяет достаточно большой динамический диапазон обнаружения слабых сигналов.

Обычные последовательности радиоимпульсов используются в радиотехнических комплексах аппаратуры редко. Они имеют большие  боковые лепестки корреляционной функции, что не позволяет обнаружение слабых импульсных последовательностей на фоне импульсной последовательности с большой амплитудой.

В настоящей работе рассмотрена методика обработки импульсных последовательностей радиоимпульсов на основе положений теории оптимального приема. При приеме двух импульсных последовательностей используется коэффициент корреляции между ними. Это позволяет учесть уровень боковых лепестков корреляционных функций импульсных последовательностей и практически исключить их отрицательное влияние.

Теоретические положения

Рассмотрим методику обработки последовательности радиоимпульсов методом максимального правдоподобия [1, 2]. Пусть принятое сообщение имеет вид:

                                    (1)

где  – комплексная амплитуда, одинаковая для всей импульсной последовательности;

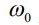 – круговая частота;

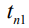 – время приема первого радиоимпульса n-последовательности. Для n-радиоимпульса выполняется условие:

                              (2)

где Т – длительность радиоимпульса;

N – количество радиоимпульсов.

На основании (1) запишем логарифм функции правдоподобия [1, 2].

                           (3)

где 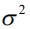  –  дисперсия шума;

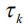 – интервал корреляции шума;

- вектор оценочных параметров сигнала.

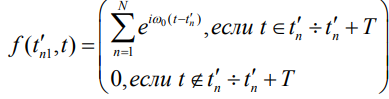 – функция, определяющая импульсную последовательность (моделирующая функция).

Для определения оптимального алгоритма обработки в соответствии с [1, 2] продифференцируем (3) по амплитуде 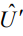 и приравняем дифференциал нулю. В результате получим

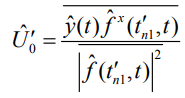                                           (4)

Чертой сверху обозначено интегрирование по времени t.

Таким образом, получено выражение, определяющее оптимальную обработку импульсной последовательности. Данное решение несмещенное.

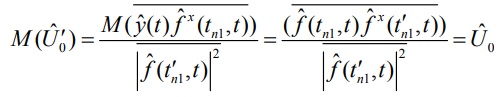.                      (5)

Математическое ожидание амплитуды  определяется корреляционной нормированной функцией модулирующей последовательности. В точке максимума корреляционной функции при 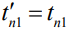 математическое ожидание .

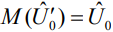Аналогично, дифференцируя логарифм функции правдоподобия (4) по времени приема первого радиоимпульса  и приравнивая дифференциал нулю, можно получить выражение, определяющее оптимальную обработку последовательности радиоимпульсов для оценки времени приема.

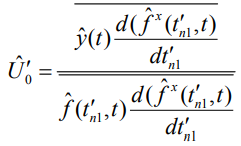                                         (6)

Рассмотрим вопрос о дисперсии амплитуды 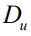 и времени приема   последовательности радиоимпульсов в точке максимума корреляционной функции. Для ее нахождения логарифм функции правдоподобия (3) дифференцируем два раза по амплитуде 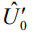 в соответствии  с  выражением для элемента информационной матрицы Фишера [1, 2, 3].

                                        (7)

где М – оператор математического ожидания.

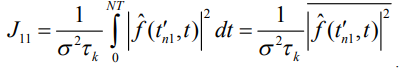                            (8)

Обратная величина определяет дисперсию амплитуды .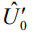

.                                               (9)

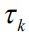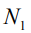Она зависит от интервала корреляции  дисперсии шума , псевдо энергии модулирующей функции . Если модулирующая последовательность состоит из «единиц» и «нулей», тогда ее энергия равна , где  – количество единиц в модулирующей последовательности. Если модулирующая последовательность состоит из положительных «единиц» и отрицательных «единиц», тогда энергия  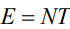( – количество радиоимпульсов). 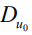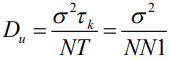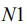В этом случае дисперсия  определяется выражением , где - количество некоррелированных отсчетов шума на интервале .

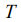Аналогично, дифференцируя логарифм функции правдоподобия по времени приема 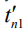 два раза, можно получить дисперсию времени приема первого радиоимпульса импульсной последовательности.

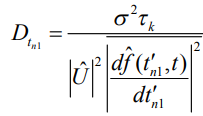                                              (10)

Определим отношение сигнал/шум в максимуме корреляционной функции для случая, когда модулирующая последовательность содержит 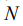 положительных и отрицательных единиц.

                                                  (11)

Таким образом, использование модулированных последовательностей радиоимпульсов дает возможность существенно повысить отношение сигнал/шум за счет увеличения длительности последовательности радиоимпульсов (базы сигнала). В этом случае отношение сигнал/шум увеличивается в 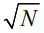 раз.

Рассмотрим вопрос о разрешении двух импульсных последовательностей, отличающихся временем приема. Импульсные последовательности имеют разные амплитуды  и разные времена приема t₁, t₂. Модуляционные последовательности одинаковы, рабочая частота также одинакова. Обозначим импульсные модуляционные последовательности 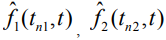 и запишем принятое сообщение в виде:

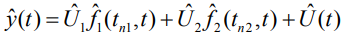                         (12)

На основании принятого сообщения запишем логарифм функции правдоподобия. Штрихами отмечены оценочные параметры.

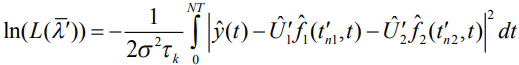            (13)

Дифференцируя (13) по амплитудам  и приравнивая дифференциалы к нулю, получим систему уравнений:

               (14)

Черта сверху означает интегрирование. Определим нормированный коэффициент корреляции:

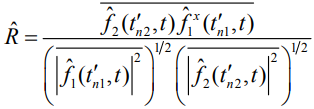                                    (15)

В этом случае решением системы уравнений (14) будет:

      (16)

При  получаем решения классического корреляционного анализа типа (4). В этом случае две последовательности радиоимпульсов ортогональны. Если 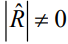, тогда последовательности неортогональны. Происходят интерференционные изменения суперпозиции двух корреляционных функций. Выражения (16) в этом случае имеют несмещенные оценки амплитуд лишь в точке  Для нахождения этих точек подставим выражения (16) в функционал правдоподобия.

                    (17)

и преобразуем его к виду

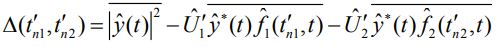                (18)

Функционал (18) представляет собой поверхность в пространстве оценочных параметров 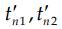. Перебирая эти параметры в пределах области определения, можно получить полную поверхность функционала, минимум которой определяет решение: .

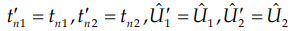Таким образом, методика нахождения решения сводится к вычислению выражений (16) при принятых значениях 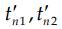, подстановке их в выражение (18), получению методом перебора параметров  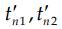поверхности функционала, оценке в минимуме поверхности значений комплексных амплитуд и времени приема двух последовательностей радиоимпульсов. По сравнению с классическим корреляционным анализом данная методика получения решения более общая. Она дает возможность получения решения при коэффициенте корреляции, отличном от нуля. Боковые лепестки при этом  полностью исключаются и не оказывают мешающего действия. Пусть коэффициент корреляции R отличен от нуля, а принятое сообщение содержит первую и вторую импульсные последовательности. В этом случае

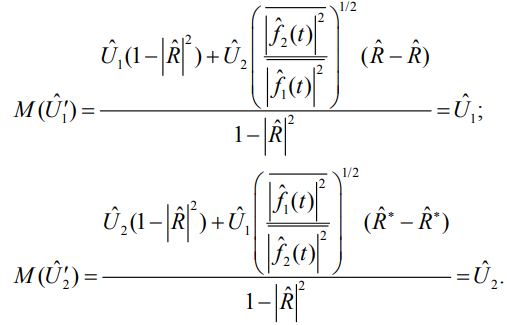                  (19)

Таким образом, решения (16) с учетом (18) не зависят от коэффициента корреляции. Это значит, что при любом сдвиге по времени τ между двумя импульсными последовательностями математическое ожидание от решений (16) дает несмещенную оценку параметров.

Рассмотрим оценку дисперсии амплитуд двух импульсных последовательностей. Для этого согласно [1, 2, 3] двойным дифференцированием логарифма функции правдоподобия (13) по амплитудам  получим элементы информационной матрицы Фишера.

                         (20)

Диагональные элементы обратной матрицы определяют дисперсии амплитуд.

                             (21)

Энергия модуляционных функций равна Е=NТ при условии, что она представлена положительными и отрицательными единицами. В этом случае выражение (19) будет

                             (22)

Где - количество некоррелированных отсчетов шума на интервале 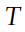. Нормируя эту дисперсию на дисперсию 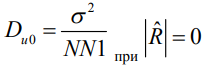, можно получить простую зависимость относительной дисперсии от коэффициента корреляции.

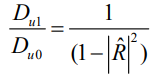                                                 (23)

На рис.1 показана зависимость среднеквадратичного отклонения амплитуд 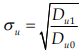 от коэффициента отражения 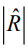. Кривая сильно увеличивается в области значений коэффициента корреляции .

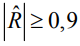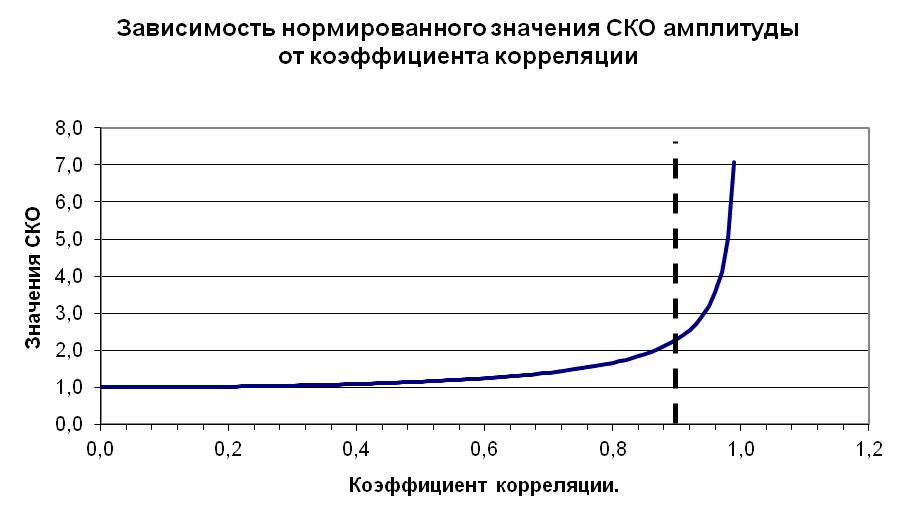
Рис. 1 – Зависимость нормированного значения СКО амплитуды от коэффициента корреляции

 

Минимальная дисперсия будет в точках, где коэффициент корреляции 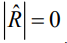  В точке, где  относительная дисперсия увеличивается на 7 дБ. Если за счет длительности модулирующей последовательности дисперсия амплитуды будет уменьшена на 7дБ, то этим обеспечивается возможность работы с корреляционной последовательностью при наличии боковых лепестков, достигающих значения .

Заключение

В настоящей работе рассмотрена методика обработки последовательности радиоимпульсов на основе положений теории оптимального приема.  Получено выражение, определяющее оптимальную обработку последовательности радиоимпульсов. Оно представляет собой корреляционную функцию, максимум которой определяет решение. Выведено выражение для оценки дисперсии амплитуды  и времени приема последовательности радиоимпульсов. Решена задача разрешения двух импульсных последовательностей с оценкой дисперсий  параметров Рао-Крамера. Показано, что разрешение двух импульсных последовательностей возможно при коэффициенте корреляции между ними, достигающем значения 0,9.