ФРЕЙМЫ ОБЩЕГО ПОЛОЖЕНИЯ ПРИ ОЦЕНКЕ ВРЕМЕНИ ВОССТАНОВЛЕНИЯ СИГНАЛОВ БЕЗ ФАЗ
Кулешова А.А.
Аспирант, Федеральное государственное автономное образовательное учреждение высшего образования «Самарский национальный исследовательский университет имени академика С.П. Королева» в г. Самара
ФРЕЙМЫ ОБЩЕГО ПОЛОЖЕНИЯ ПРИ ОЦЕНКЕ ВРЕМЕНИ ВОССТАНОВЛЕНИЯ СИГНАЛОВ БЕЗ ФАЗ
Аннотация
Поиск быстрых алгоритмов для восстановления сигнала без фазы актуален в настоящее время. Алгоритмы восстановления важны в обработке разнообразных сигналов, в особенности в технологии распознавания речи, в томографии. Главное свойство фреймов, которое делает их настолько полезными в прикладных задачах – их избыточность. Хорошо выбранный фрейм может обеспечить численную устойчивость для восстановления сигнала и получение важных характеристик сигнала. Семейство фреймов восстанавливает сигнал по абсолютному значению фреймовых коэффициентов в полиномиальное время.
Ключевые слова: фрейм, восстановление сигнала без фаз, равномерные фреймы.
Kuleshova A.A.
Postgraduate student, Samara University in Samara
GENERAL FRAMES AT THE ASSESSMENT OF THE TIME OF FOR SIGNAL RECONSTRUCTION WITHOUT PHASE
Abstract
Search of fast algorithms for doing signal reconstruction without phase is actual now. Algo-rithms of signal reconstruction are important in handling of various signals, in particular from speech recognition technology , in a tomography. The main property of frames which makes them so useful in applied problems is their redundancy. In general, a carefully chosen frame can provide numerical stability for reconstruction and an ability to capture important signal characteristics. The family of frames signal reconstruction on absolute value of frame coefficients in polynomial time.
Keywords: frame, reconstruction without phase, uniform frames.
Дискретизация и квантование аналогового сигнала дают возможность рассматривать сигнал как элемент конечномерного пространства V [1, C. 280].
По ортонормированному базису ![]() «сигнал»
«сигнал» ![]() единственным образом может быть записан как сумма:
единственным образом может быть записан как сумма:
![]()
Представляя сигнал в различных базисах, можно получить о нем разнообразную информацию. Так, переход от представления по ортам к представлению в базисе Фурье, позволяет получить частотные характеристики сигнала, дающие широкие возможности для его цифровой обработки.
Последние годы большое количество работ посвящено решению следующей задачи: найти такие системы «измерительных» векторов ![]() , которые позволяют восстановить произвольный сигнал
, которые позволяют восстановить произвольный сигнал ![]() по набору вещественных чисел
по набору вещественных чисел ![]() .
.
Была доказана теоретическая возможность точного восстановления сигнала, если в качестве системы представления используются полные избыточные системы [2, P. 354].
Определение 1: Семейство векторов ![]() называется фреймом гильбертового пространства HN, если существуют константы А, В: 0 < A ≤ B < ∞, такие, что для всех x ∈ H выполняются следующие неравенства:
называется фреймом гильбертового пространства HN, если существуют константы А, В: 0 < A ≤ B < ∞, такие, что для всех x ∈ H выполняются следующие неравенства:
![]()
A и B называются границами фрейма. Если A=B, то фрейм называется А-жестким, а если A=B=1, то фреймом Парсеваля-Cтеклова.
Числа ![]() называются фреймовыми коэффициентами.
называются фреймовыми коэффициентами.
Определение 2: Пусть ![]() - фрейм, линейное отображение:
- фрейм, линейное отображение:
![]()
называется оператором анализа.
Определение 3: Линейное отображение:
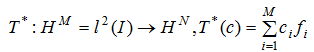
называется оператором синтеза.
Композиция отображений ![]() и
и ![]() определяет фреймовый оператор – положительный, самосопряженный обратимый оператор:
определяет фреймовый оператор – положительный, самосопряженный обратимый оператор:
![]()
Оператор S обеспечивает точную формулу для восстановления:
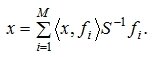
Рассмотрим P - такое нелинейное отображение, переводящее вектор в набор модулей фреймовых коэффициентов:
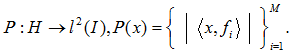
Если необходимо связать P с некоторым фреймом ![]() , то запишем:
, то запишем: ![]() .
.
Пусть ![]() - фактор-пространство, полученное отождествлением двух векторов, если они отличаются постоянным фазовым коэффициентом. Таким образом, x~y означает, что существует такая константа c: |c|=1 , что y=cx.
- фактор-пространство, полученное отождествлением двух векторов, если они отличаются постоянным фазовым коэффициентом. Таким образом, x~y означает, что существует такая константа c: |c|=1 , что y=cx.
Для вещественных Гильбертовых пространств ![]() , тогда
, тогда ![]() .
.
Для комплексных гильбертовых пространств ![]() , тогда
, тогда ![]() , где
, где ![]() - окружность единичного радиуса на комплексной плоскости.
- окружность единичного радиуса на комплексной плоскости.
Нелинейное отображение P на ![]() действует так:
действует так:
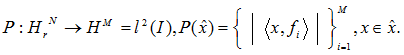
Если ![]() , множество I состоит из М-элементов,
, множество I состоит из М-элементов, ![]() . Тогда
. Тогда ![]() .
.
Рассмотрим множество ![]() – это множество N-мерных линейных подпространств в
– это множество N-мерных линейных подпространств в ![]() , которое имеет структуру
, которое имеет структуру ![]() -мерного множества.
-мерного множества.
Множество ![]() называется многообразием Грассмана.
называется многообразием Грассмана.
Для фрейма ![]() оператор анализа удовлетворяет:
оператор анализа удовлетворяет:
![]()
где ![]() – канонический базис в
– канонический базис в ![]() .
.
Рассматриваемое нелинейное отображение в вещественном случае:
![]()
Если ![]() , то для M-элементов фрейма
, то для M-элементов фрейма ![]() оператор анализа:
оператор анализа:
![]()
Скалярное произведение по определению: ![]()
Нелинейное отображение:
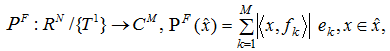
где два вектора ![]() , если существует такая константа
, если существует такая константа ![]() , такая что
, такая что ![]() .
.
Фреймы общего положения восстанавливают сигналы без фаз [1] и это восстановление достигается за полиномиальное время.
Определение 4: Фрейм ![]() называется фреймом общего положения, если
называется фреймом общего положения, если ![]() , где U – открытое по Зарисскому множество и
, где U – открытое по Зарисскому множество и ![]() .
.
Теорема 1: (Вещественный случай) [3] Если ![]() , то для фрейма общего положения
, то для фрейма общего положения ![]() , нелинейное отображение P инъективно.
, нелинейное отображение P инъективно.
Доказательство: Предположим, что ![]() и
и ![]() имеют одинаковый образ при нелинейном отображении P. Пусть
имеют одинаковый образ при нелинейном отображении P. Пусть ![]() – фреймовые коэффициенты для
– фреймовые коэффициенты для ![]() и
и ![]() – фреймовые коэффициенты для
– фреймовые коэффициенты для ![]() . Тогда
. Тогда ![]() для каждого
для каждого ![]() .
.
В частности, существует подмножество индексов ![]() таких, что
таких, что ![]() . Тогда два вектора
. Тогда два вектора ![]() и
и ![]() имеют одинаковый образ при отображении P тогда и только тогда, когда существует подмножество
имеют одинаковый образ при отображении P тогда и только тогда, когда существует подмножество ![]() , такое что оба набора фреймовых коэффициентов
, такое что оба набора фреймовых коэффициентов ![]() и
и ![]() находятся в некотором множестве
находятся в некотором множестве ![]() .
.
Для завершения доказательства мы покажем, что при ![]() такое условие невозможно для подпространств общего положения
такое условие невозможно для подпространств общего положения ![]() .
.
Это означает, что множество таких подпространств ![]() представляет собой плотное открытое по Зарискому множество на многообразии Грассмана Gr(N, M). В частности, вероятность того, что случайно выбранное
представляет собой плотное открытое по Зарискому множество на многообразии Грассмана Gr(N, M). В частности, вероятность того, что случайно выбранное ![]() будет удовлетворять этому условию, равна 0.
будет удовлетворять этому условию, равна 0.
Для завершения доказательства теоремы нам понадобится следующая лемма.
Лемма 1: Если ![]() , то справедливо следующее утверждение для N-мерного подпространства общего положения
, то справедливо следующее утверждение для N-мерного подпространства общего положения ![]() : пусть
: пусть ![]() , тогда
, тогда ![]() тогда и только тогда, когда
тогда и только тогда, когда ![]() .
.
Доказательство: Предположим, что ![]() .
.
Так как ![]() - инволюция, то
- инволюция, то ![]() фиксировано и отлично от нуля. Таким образом,
фиксировано и отлично от нуля. Таким образом, ![]() .
.
Аналогично
![]()
Следовательно, ![]() .
.
Тогда ![]() и
и ![]() - фиксированные линейные подпространства размерности
- фиксированные линейные подпространства размерности ![]() и
и ![]() соответственно. Если
соответственно. Если ![]() , то одно из этих подпространств является подпространством коразмерности больше или равной
, то одно из этих подпространств является подпространством коразмерности больше или равной ![]() . Однако линейное подпространство общего положения
. Однако линейное подпространство общего положения ![]() размерности
размерности ![]() имеет нулевое пересечение с фиксированным линейным подпространством коразмерности больше или равной
имеет нулевое пересечение с фиксированным линейным подпространством коразмерности больше или равной ![]()
![]() .
.
Поэтому, если ![]() - подпространство общего положения и для
- подпространство общего положения и для ![]() , тогда
, тогда ![]() .
.
Доказательство теоремы следует из того, что если ![]() находится в пересечении общих условий, налагаемых предложением для каждого подмножества
находится в пересечении общих условий, налагаемых предложением для каждого подмножества ![]() , то
, то ![]() удовлетворяет заключению теоремы.
удовлетворяет заключению теоремы.
Определение 5: Набор векторов ![]() в
в ![]() назовем альтернативно полным, если для любого
назовем альтернативно полным, если для любого ![]() , либо
, либо ![]() , либо
, либо ![]() полно в
полно в ![]() .
.
Теорема 2: Пусть ![]() - набор векторов в
- набор векторов в ![]() . Отображение
. Отображение ![]() определено равенствами:
определено равенствами: ![]() . Тогда отображение
. Тогда отображение ![]() инъективно тогда и только тогда, когда F- альтернативно полно.
инъективно тогда и только тогда, когда F- альтернативно полно.
Доказательство:
(⇒) Предположим, что F - не альтернативно полно. Следовательно, найдется ![]() такое, что ни
такое, что ни ![]() , ни
, ни ![]() не полно в
не полно в ![]() .
.
Выбираем ненулевые векторы ![]() так, что
так, что ![]() для всех
для всех ![]() и
и ![]() для всех
для всех ![]() . Для каждого
. Для каждого ![]() имеем:
имеем:
![]()
Отсюда следует, что ![]() для каждого
для каждого ![]() , и
, и ![]() . Более того, так как
. Более того, так как ![]() и
и ![]() ненулевые, по предположению, то и
ненулевые, по предположению, то и ![]() . Таким образом, инъективности отображения
. Таким образом, инъективности отображения ![]() нет.
нет.
(⇐) Предположим, что ![]() не инъективно. Это означает, что существуют векторы
не инъективно. Это означает, что существуют векторы ![]() такие, что
такие, что ![]() и
и ![]() . Обозначим
. Обозначим ![]() .
.
Имеем:![]() для каждого
для каждого ![]() . Иначе, если
. Иначе, если ![]() тогда
тогда ![]() и тогда
и тогда ![]() . По предположению,
. По предположению, ![]() , поэтому
, поэтому ![]() . Таким образом, и
. Таким образом, и ![]() не полны в
не полны в ![]() .
.
Определение 6: Множество ![]() называется набором с полным спарком, если каждое его подмножество из N векторов полно в
называется набором с полным спарком, если каждое его подмножество из N векторов полно в ![]() .
.
Теорема 3: В вещественном случае, если ![]() в
в ![]() и
и ![]() , то отображение
, то отображение ![]() не является инъективным. Если
не является инъективным. Если ![]() , то отображение
, то отображение ![]() инъективно тогда и только тогда, когда
инъективно тогда и только тогда, когда ![]() - полный спарк.
- полный спарк.
Следствие 1: Если F это М–элементный фрейм в ![]() с
с ![]() и у
и у ![]() каждые N-элементов фрейма линейно независимы, то оператор
каждые N-элементов фрейма линейно независимы, то оператор ![]() - инъективен.
- инъективен.
Примером такого фрейма является фрейм Мерседес-Бенц в ![]() , состоящий из 3-х векторов единичной длины, расположенных под углом 120º.
, состоящий из 3-х векторов единичной длины, расположенных под углом 120º.
Теорема 4: (Комплексный случай) Если M≥4N-2, то для фрейма общего положения F, отображение ![]() инъективно.
инъективно.
Теорема 5 [3],[5, P.372]: Пусть H – фиксированное N-мерное векторное пространство (вещественное или комплексное), пусть ![]() – ортонормированный базис для H.
– ортонормированный базис для H.
(а) Если ![]() ,
, ![]() и
и ![]() – фрейм общего положения, нелинейное отображение P – инъективно. Тогда вектор
– фрейм общего положения, нелинейное отображение P – инъективно. Тогда вектор ![]() может быть восстановлен (с точностью до знака) из множества
может быть восстановлен (с точностью до знака) из множества 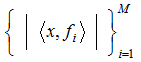 модулей фреймовых коэффициентов за полиномиальное число шагов
модулей фреймовых коэффициентов за полиномиальное число шагов ![]() .
.
(б) Если ![]() – фрейм общего положения, нелинейное отображение P – инъективно. Тогда вектор
– фрейм общего положения, нелинейное отображение P – инъективно. Тогда вектор ![]() может быть восстановлен (с точностью умножения на корень из единицы) из множества
может быть восстановлен (с точностью умножения на корень из единицы) из множества 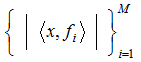 модулей фреймовых коэффициентов за полиномиальное число шагов
модулей фреймовых коэффициентов за полиномиальное число шагов ![]() .
.
Список литературы / References
- Новиков С.Я. Полные системы в задачах восстановления сигнала / Новиков С.Я., Федина М.Е. // Труды Международной научно-технической конференции, Том 1 «Перспективные информационные технологии» – 2015. – С. 280–283.
- Balan. Fast algorithems for signal reconstruction without phase / R. Balan , B. G. Bodmann, P. G. Casazza, D. Edidin // Proceedings of SPIE-Wavelets XII, San Diego 6701 (2007) 670111920-670111932
- Balan. Painless reconstruction from magnitudes of frame coefficients, preprint / R. Balan, B. G. Bodman, P. G. Casazza and D. Edidin.
- Balan. On signal reconstruction without phase / R. Balan, P. Casazza, D. Edidin // Appl.Comput.Harmon.Anal. 20 –2006 – P. 345–356.
- Kuleshova A. [Electronic resource] Generic frame in problems for signal reconstruction without phase // ITNT 2016 Information Technology and Nanotechnology – 2016.– P. 364-372. – URL: http://ceur-ws.org/Vol-1638/
Список литературы на английском языке / References in English
- Novikov S.J. Polnye sistemy v zadachah vosstanovlenija signala [Complete systems in problems of signal reconstruction] / Novikov S.J., Fedina M.E. // Trudy Mezhdunarodnoj nauchno-tehnicheskoj konferencii, Tom 1 «Perspektivnye informacionnye tehnologii» [Proceedings of the International Scientific and Technical Conference, Volume 1 "Perspective Information Technologies"] – 2015. – P. 280–283. [in Russian]
- R. Balan. Fast algorithems for signal reconstruction without phase / R. Balan , B. G. Bodmann, P. G. Casazza, D. Edidin // Proceedings of SPIE-Wavelets XII, San Diego 6701 (2007) 670111920-670111932
- R. Balan. Painless reconstruction from magnitudes of frame coefficients, preprint / R. Balan, B. G. Bodman, P. G. Casazza and D. Edidin.
- R. Balan. On signal reconstruction without phase / R. Balan, P. Casazza, D. Edidin // Appl.Comput.Harmon.Anal. 20 – 2006 – P. 345–356.
- A. Kuleshova [Electronic resource] Generic frame in problems for signal reconstruction witho
