О ЗАКОНОМЕРНОСТЯХ ДВИЖЕНИЯ ПЛАНЕТ

Кораблев Г.А.

Доктор химических наук, профессор, Ижевская государственная сельскохозяйственная академия, Ижевск, Россия

О ЗАКОНОМЕРНОСТЯХ ДВИЖЕНИЯ ПЛАНЕТ

Аннотация

Модифицируя уравнение Кеплера по орбитальным движениям планет даны уравнения зависимости вращательного и орбитального движений планет, рассчитаны углы их вращения. Установлены волновые принципы прямого и обратного вращения планет. Установленные зависимости проявляются на различных масштабных уровнях структурных взаимодействий, в том числе в биосистемах. Равенство углов вращения Солнца и Земли через резонанс корпускулярно-волнового механизма определяет возможность земного фотосинтеза. Точность расчетов соответствует точности экспериментальных данных.

Ключевые слова: Орбитальное и вращательное движения планет, прямое и обратное вращение планет, углы вращения, фотосинтез.

Korablev G.A.

PhD in Chemistry, Izhevsk State Agricultural Academy, Izhevsk, Russia

ABOUT THE LAWS OF MOVEMENT OF PLANETS

Abstract

By modifying the equation of Kepler from the orbital motions of the planets, equations of dependence of rotational and orbital motions of planets are given, their rotation angles are calculated. Wave principles of direct and reverse rotation of planets are established. The established dependencies are demonstrated at different scale levels of structural interactions, in biosystems as well. Equality of the Sun and Earth's rotation angles through the resonance of the wave-mechanism determines the possibility of terrestrial photosynthesis. The accuracy of calculations corresponds to the accuracy of experimental data.

Keywords: orbital and rotational motion of planets, direct and reverse rotation of planets, rotation angles, photosynthesis.

Introduction

The world around us is in constant motion. Functionally interconnected main types of mechanical motion (translational, rotational and oscillatory) determine the dynamic stability of systems. Vast theoretical and experimental experience in physical and mathematical properties of simple and complex compounds and principles of their self-organization at different scale levels of such conformation has been gained till now.

But the problem of establishing the most general regularities of these processes is topical. “However the science is still far from making it happen in the general form” [1]. Thus, applying the entire set of analytical and qualitative methods, the celestial mechanics provides the solution for many problems on the motion of solids, for example [2,3]. But some other issues of celestial mechanics require further discussion, for instance, the functional dependence of rotational and orbital motion of planets, as well as the initial principles of forming the direct and reverse motion of planets. Therefore in this paper we attempt to investigate such problematic issues with the help of conception of corpuscular-wave dualism proposed earlier [4].

1. Initial criteria

(Based on paper [4])

1. In the systems in which the interaction proceeds along the potential gradient (positive work), the resultant potential energy is found based on the principle of adding reciprocals of corresponding energies of subsystems. Similarly, the reduced mass for the relative motion of the isolated systems of two particles is calculated.
2. In the systems in which the interactions proceed against the potential gradient (negative performance) the algebraic addition of their masses, as well as the corresponding energies of subsystems is performed (similar to Hamiltonian).
3. Two principles of adding energy characteristics of structural interactions can be transformed onto the corpuscular-wave dualism processes.

Corpuscular processes flow in all interactions along the potential gradient, and wave dualism corresponds to the interactions against the potential gradient.

4. Act of quantum action expressed via Plank’s constant is narrowed to the energy equilibrium-exchange redistribution between the corpuscular and wave processes.
5. Phase difference of electric and magnetic oscillations in electromagnetic wave is . Applying 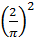 as the proportionality coefficient, we have the equation for Plank’s constant with the accuracy close to the accuracy of the initial data:

 ,

where а₀ = 0.0023293 – experimental quantum correction to spin g_s – factor, ɛ – electric constant, µ – magnetic constant. Here: P_e = wr, where w – energy of a free electron, r – its classic radius.

6. It is assumed that during the rotational-translation motion of an electron, the energies are redistributed in the system “particle-wave” that is demonstrated via the angular vector of such motion (winding angle) – ϴ.

This angular vector of electron motion is quantized by an integer number through the tangent square of this angle: tg²φ_г = 2; tg²60º = 3; tg²45º = 1, where φ_г = 54.73⁰ – a so-called “geodesic angle”, which is widely spread in engineering, for example, in spaceship production.

The quantum functions of square tangent k = 1, 2, 3 numerically determine the ratios of two triangle legs, whose values characterize energy dependencies via axial and circumferential stresses in the system with corpuscular and wave processes.

7. In quantum mechanics the ratio between the particle magnetic moment and its mechanical moment is the magnetomechanic ratio – g. At the same time, g_s = 2, if the electron magnetic moment is conditioned only by the spin component and g = 1, if it is produced by the electron orbital motion. Their ratio g_s / g = 2 that, the same way as tg²φ_г = 2, characterizes the corresponding corpuscular-wave dependencies in this approach.

 

2. Equation of dependence of rotational and orbital motion of planets

The foregoing principles of corpuscular-wave mechanism give the possibility to consider from the unified positions many structural and dynamic processes, different in nature and scale. For example, the characteristic of spin-orbital interaction – fine structure constant , where r – electron classic radius, λ – its Compton wavelength.

Formally, but similarly: interaction force of two long conductors with the current proportionally to the ratio  , where l – length of conductors, r – distance between them.

And the number 2π widely used in physical regularities, equals the circumference ratio to its radius: 2π = l / R.

In these examples, as in many other, this approach allows evaluating structural interactions based on the ratios of corpuscular and wave spatial-energy parameters in each action. Obviously, such principles are also demonstrated in Kepler’s third law, which can be given as follows [3]:

       (1)

where: G – gravitational constant, m – planet mass, here a – distance to barycenter (system mass center), T – planet revolution period. Entering the relative mass  (where m_з – Earth mass), we can have:

, therefore  = const

Or:   = const      (2)

Since the masses of planets are rather small in comparison with their distance to the sun, then at the first approximation they can be considered as mathematical points and the equation of mathematical pendulum period can be applied to them:

,

where g – free fall acceleration. The average radius of the planet orbital motion – R can be taken as the pendulum length – l. Then, similarly to the foregoing dependencies, we can introduce the planet radius r into the numerator of formula (2) and then we have:

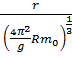= γ        (3)

This expression in the units  satisfies the principle of corpuscular-wave mechanism for space macrostructures. But in Kepler’s third law only the orbital motion was considered, but in this case – two motions, each of which has its own wave part. Therefore, the interference of coherent waves occurs.

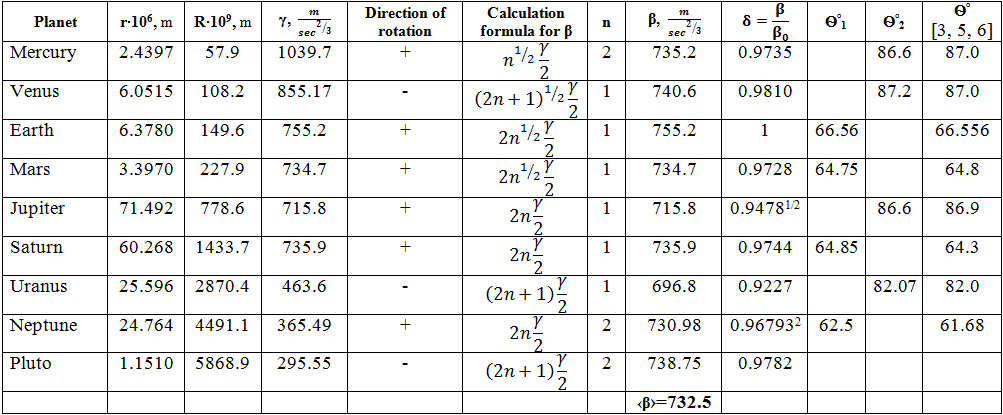
Similar to the foregoing examples, the coherence can be considered as the ratio of the difference of the travel path to the length of the coherent wave . The interference principle is most easily performed for liquid-gaseous planets (planets in Jupiter system) as shown in Table 1:

Table 1 - Characteristics of rotational and orbital motion of planets

              (4)

 – boosting of oscillations during the direct rotation of planets.

                  (5)

– damping of oscillations during the reverse rotation of planets.

Here n – integer number.

The intensity of wave propagation depends on the medium density and its distribution in the planet volume.

The value characterizing the planet density increase towards its center is called “dimensionless moment of inertia” (I^*). The ratio of average values of I^* for solid and liquid-gaseous planets based on different data [3,5,6] is within 1.4 – 1.45 as demonstrated in Table 2.

Table 2 – Ratio of dimensionless moments of inertia of solid and liquid-gaseous planets [3, 5]

Planet	Mercury	Venus	Earth	Mars	‹I*S›
I*S	0.324	0.333	0.33076	0.377	0.341
Planet	Jupiter	Saturn	Uranus	Neptune	‹I*LG›
I*LG	0.20	0.22	0.23	0.29	0.235

The average value I^*_S /I^*_LG=1.451

Such property for solid planets is taken into account in Table 1 and equations (4, 5) by introducing the values  and ( . Such approach also refers to Mercury as it is the nearest to the sun, to its liquid-gaseous structure.

In general, the application of corpuscular-wave mechanism to space macrosystems explains the specifics of formation of direct or reverse rotation of the planets.

3. Rotation angles of planets

In physical sense, the parameter β characterizes the motion difference of interfering waves, and γ – wavelength. The average value of β = 732.5 m/sec^2/3 with the deviation of most of the planets under 2 % (apart from Uranus).

The equation tg² ϴ = k was used to evaluate quantum transitions in atoms in [4]. The squares and cubes of initial parameters are applied in Kepler’s equation and other regularities of space macrosystems. In this approach, as the calculations demonstrated, the semi-empirical equation is performed:

                    (6)

where ϴ – rotation angle of planets.

For Earth β = 755.2 and based on equation (6) ϴ₀ = 66.455^º. For more accurate calculation, taking into account some analogy of macro- and microprocesses, we use, as before, the experimental quantum correction in the form of a₀ = 1.0023293 following the equation:

                   (7)

The calculation by equations for Earth (6,7) gives the value 66.560º with the deviation from the experimental value by 0.007%. The sun has the same value of the rotation angle.  This is determined by the process of the earth's photosynthesis.

As applicable to the rest of the planets, the value , (where β₀ – β value for Earth) is introduced in equation (7) based on the following equations:

   or                   (8)  (8а)

    or                   (9) (9а)

The formulas (8 and 8а) are performed for the planets, whose rotation angle is less than Earth’s one. For the other planets the formulas (9 and 9а) are performed. Those are the planets, which are in the beginning of the planet subsystem by the value of the dimensionless moment of inertia (Mercury and Jupiter), as well as the planets with the reverse rotation (Venus and Uranus). The calculation results are given in Table 1.

The coefficient  has been applied before for the comparative evaluation of quantum transitions with different complexity types [4]. In this research the average ratio of the angles by the experimental data  [3,5,6] given in Table 3 also has the value 1.336 ≈  .

Table 3 – Ratio of rotation angles of planets by [3, 5, 6]

Planet	Mercury	Venus	Earth	Mars	‹Ѳ2›
Ѳ2	87.00	87.00	86.90	82.00	85.73
Planet	Jupiter	Saturn	Uranus	Neptune	‹Ѳ1›
Ѳ1	66.556	64.80	64.30	61.00	64.16

The average value Ѳ₂/Ѳ₁ = 1.336 ≈  

For the value  the influence of the medium density distribution is taken into account via the transition factor from one distribution level to another. Since for Jupiter in Table 2 the value I^* is less in comparison with Earth’s I^* in 1.45 times, therefore, in the calculations  = 0.9478^1/2. On the contrary with Jupiter, for Neptune I^* increases in 1.45 times, therefore, in the calculations  = 0.96793².

All the calculation results are in good accord with the experimental data.

Список литературы / References

1. Эрден-Груз Т. Основы строения материи / Т. Эрден-Груз // М.: Мир, 1976. – 438 с.
2. Дубошин Г.Н. Небесная механика / Г.Н. Дубошин // М.: Наука, 1978. – 456 с.
3. Пантелеев В.Л. Физика Земли и планет. Курс лекций / В.Л. Пантелеев // МГУ. Москва, 2001.
4. G.А. Korablev. Spatial-energy parameter and its application in research. LAP LAMBERT Academic Publishing. Germany. Рр. 1-65.
5. Физическая энциклопедия. М.: «Советская энциклопедия». Т.1, 1988. – 704 с.; Т.2, 1990. – 704 с.; Т.3, М.: «Большая Российская энциклопедия». 1992. – 672 с.
6. Аллен К.У. Астрофизические величины / К.У. Аллен // М.: Изд. «МИР», 1977. – 446 с.

Список литературы на английском языке / References in English

1. Jerden-Gruz T. Osnovy stroenija materii [Basics of matter composition] / Т. Jerden-Gruz // М.: Mir, 1976. – 438 p. [in Russian]
2. Duboshin G.N. Nebesnaja mehanika [Celestial mechanics] / G.N. Duboshin // М.: Nauka, 1978. – 456 p. [in Russian]
3. Panteleev V.L. Fizika Zemli i planet. Kurs lekcij [Physics of Earth and planets. Lectures] / V.L. Panteleev // MGU. Moskva [MSU. Moscow], 2001. [in Russian] http://www.astronet.ru/db/msg/1169697/node17.html
4. G.А. Korablev. Spatial-energy parameter and its application in research. LAP LAMBERT Academic Publishing. Germany. Рр. 1-65.
5. Fizicheskaja jenciklopedija [Encyclopedia in physics]. M.: «Sovetskaja jenciklopedija» [“Sovetskaya enciklopedia”]. V.1, 1988. – 704 p.; V.2, 1990. – 704 p.; V.3, M.: «Bol'shaja Rossijskaja jenciklopedija» [“Bolshaja Rossijskaja enciklopedia”]. 1992. – 672 p. [in Russian]
6. Allen K.U. Astrofizicheskie velichiny [Astrophysical magnitudes] / K.U. Allen // M.: Izd. «MIR» [М.: Мir], 1977. – 446 p. [in Russian]