РЕАЛИЗАЦИЯ ОПТИМАЛЬНОГО АЛГОРИТМА УСТРАНЕНИЯ НЕОДНОЗНАЧНОСТИ ФАЗОВЫХ ИЗМЕРЕНИЙ

Губаренко М. А.

Аспирант,

Омский государственный технический университет

РЕАЛИЗАЦИЯ ОПТИМАЛЬНОГО АЛГОРИТМА УСТРАНЕНИЯ НЕОДНОЗНАЧНОСТИ ФАЗОВЫХ ИЗМЕРЕНИЙ

Аннотация

Рассмотрен метод определения направления на источник излучения. Азимут и угол места определены на основании оптимального алгоритма. Восстановлена неоднозначность фазовых измерений. В статье определена область применения  рассмотренного метода восстановления вектора неоднозначности.

Ключевые слова: фаза, оптимальный алгоритм, неоднозначность фазы, область применения.

Gubarenko M. A.

Postgraduate student,

Omsk state technical university

IMPLEMENTATION OF OPTIMAL ALGORITHM RESTORING AMBIGUITY OF PHASE

Abstract

Determination the direction in the line of  emission source is considered in the article. Azimuth and tilt angle are defined by the use of optimal algorithm. Ambiguity of phase measuring is restored. Article determines field of application considered method  of  restoring the vector.

Keywords: phase, optimal algorithm, ambiguity of phase, field of application.

Источниками радиосигналов могут быть объекты радиолокационного наблюдения, отражающие радиоволны, либо различного рода радиопередатчики. Информация о направлении прихода к пеленгатору излученной волны содержится в положении её фазового фронта. Нормаль к фазовому фронту в однородной среде распространения радиоволн совпадает с направлением на источник излучения.

Диаграмма направленности приемной антенны зависит от назначения фазового пеленгатора. В следящих пеленгаторах, предназначенных для работы по выбранным источникам сигналов, применяются направленные антенны. Применение таких антенн, с одной стороны, увеличивает соотношение сигнал/собственный шум приемных устройств, с другой ограничивает измеряемую разность фаз интервалом 360 градусов.

Использование радиопеленгаторов в составе систем радиоэлектронной борьбы сопряжено с некоторыми техническими трудностями. В частности с априорной неопределенностью несущей частоты. В рамках данной работы будем считать, что несущая частота была определена ранее и может быть использована в расчетах.

Использование разности фаз приемных антенн фазового пеленгатора позволяет определить направление на источник излучения. Существуют различные алгоритмы для определения азимута и угла места. Основное отличие методов заключается в способе поиска векторов неоднозначности.

Алгоритм максимального правдоподобия (оптимальный алгоритм) имеет наибольшую вероятность правильного устранения неоднозначности и требует больших вычислительных ресурсов.

Квазиоптимальный алгоритм устраняет неоднозначность фазовых измерений с меньшей вероятностью. Собственные области векторов неоднозначности аппроксимируются параллелепипедами, что упрощает процедуру поиска векторов, однако снижает вероятность правильного устранения неоднозначности.

В работе построена модель двухкоординатного фазового пеленгатора с плоской антенной решеткой. Для нахождения вектора неоднозначности фазовых измерений реализована модификация алгоритма максимального правдоподобия при условии, что поиск вектора неоднозначности ведется перебором всех возможных вариантов.

Будем считать, что погрешности фазовых измерений подчиняются нормальному закону распределения вероятностей, имеют нулевые средние значения. На основании этого [1, с. 168] вычислена корреляционная матрица фазовых ошибок . Рассмотрено решение системы уравнений правдоподобия:

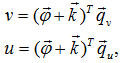
 где весовые векторы    вычислены через матрицу , обладающую свойством . Эта матрица введена В. И. Беловым в работе [2, с. 98]. Весовые векторы [1, с. 166] найдены из следующих равенств:

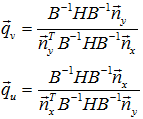
Вектор неоднозначности  выбирается таким, чтобы функция правдоподобия , описанная в [1, с. 165], достигала главного максимума. Там же показано, что для сокращения объема вычислений достаточно найти минимум показателя степени  в функции правдоподобия, что и сделано в настоящей работе.

Далее выполнен поиск вектора неоднозначности  для которого функция  достигает минимального значения. Выбраны 5 антенных баз [3, с. 8], характеризующихся векторами относительных баз    [4, с. 186]. Тогда очевидно, что вектор  может находиться в диапазоне от  . Выполнен поиск целочисленного вектора  с шагом , построена зависимость  от рассмотренных векторов  :

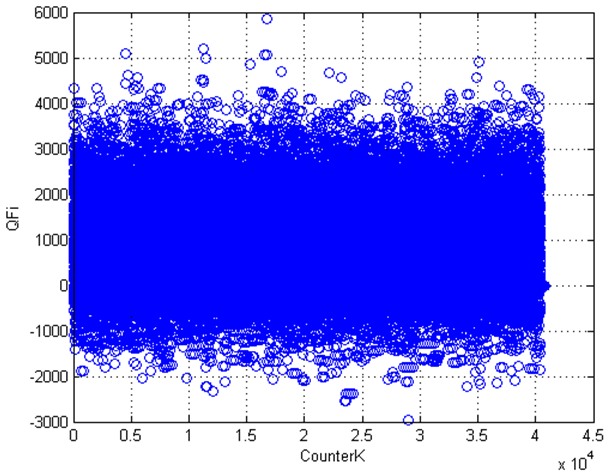
Рис. 1 График функции 

На рисунке 1  - порядковый номер вектора неоднозначности, для которого вычислено значение функции .

Согласно графику   достигает минимума для некоторого вектора . Этот вектор выбран в качестве искомого вектора неоднозначности. Используя этот вектор, восстановлена полная фаза  принятой волны [1, с. 165] и найдены направляющие косинусы   . Далее найдены азимут α и угол места β:

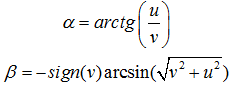
Алгоритм протестирован для азимута  и угла места . Выявлено, что при частотах принимаемой волны просматриваются не  все вектора неоднозначности. Это приводит к нахождению вместо глобального максимума одного из локальных минимумов показателя степени  функции правдоподобия.

Найти пропущенные вектора, можно уменьшив шаг сетки . Однако это приводит к существенному увеличению времени на поиск вектора. Это обстоятельство ограничивает область применимости метода выбора векторов неоднозначности путем вычисления  на каждом возможном векторе. Метод поиска по всей области векторов применим для частот принимаемой волны .

Литература

1. Денисов,В. П., Дубинин Д. В. Фазовые радиопеленгаторы. Томск: издательство ТГУ, 2002, 251 с.
2. БеловВ. И. Теория фазовых измерительных систем Томск: издательство ТГУ, 2007, 148 с.
3. Сколник М. Справочник по радиолокации. М.: Советское радио, 1976, 456 с.
4. Старр А. Радиотехника и радиолокация М.: Советское радио, 1960, 668 с.

References

1. Denisov, V. P., Dubinin D. V. Fazovye radiopelengatory. Tomsk: izdatel'stvo TGU, 2002, 251 s.
2. Belov V. I. Teorija fazovyh izmeritel'nyh sistem Tomsk: izdatel'stvo TGU, 2007, 148 s.
3. Skolnik M. Spravochnik po radiolokacii. M.: Sovetskoe radio, 1976, 456 s.
4. Starr A. Radiotehnika i radiolokacija M.: Sovetskoe radio, 1960, 668 s.