КОНСТРУИРОВАНИЕ СИСТЕМЫ ЗАДАЧ ПО АЛГЕБРЕ И НАЧАЛАМ МАТЕМАТИЧЕСКОГО АНАЛИЗА В СООТВЕТСТВИИ С ЭТАПАМИ УСВОЕНИЯ УЧАЩИМИСЯ ЗНАНИЙ

Аммосова Н.А.¹, Краснова Г.Г.²

¹Доктор педагогических наук,

²Аспирант,

Астраханский государственный университет

КОНСТРУИРОВАНИЕ СИСТЕМЫ ЗАДАЧ ПО АЛГЕБРЕ И НАЧАЛАМ МАТЕМАТИЧЕСКОГО АНАЛИЗА В СООТВЕТСТВИИ С ЭТАПАМИ УСВОЕНИЯ УЧАЩИМИСЯ ЗНАНИЙ

Аннотация

В статье рассмотрено конструирование системы алгебраических задач в соответствии с  тремя уровнями усвоения школьниками математических знаний, приведена характеристика задач каждого уровня и примеры задач, соответствующие второму уровню усвоения знаний, по теме «Логарифмическая функция».

Ключевые слова: конструирование, система задач, усвоение, логарифмическая функция.

Ammosova N.A.¹, Krasnova G.G.²

¹Doctor of Pedagogical Sciences,

²Aspirant,

Astrakhan State University

DESIGNING OF SYSTEM OF TASKS OF ALGEBRA AND OF THE BEGINNINGS OF THE MATHEMATICAL ANALYSIS ACCORDING TO STAGES OF ASSIMILATION BY PUPILS OF KNOWLEDGE

Abstract

The paper considers the design of a system of algebraic tasks in accordance with the three levels of schoolchildren mastering mathematical knowledge,  shows the characteristics of tasks of each level and examples of tasks corresponding to the second level of learning, on the theme "The logarithmic function".

Keywords: designing, system of tasks, digestion, logarithmic function.

В последние десятилетия в методических исследованиях особое внимание уделяется конструированию различных совокупностей взаимосвязанных задач. В методической литературе используются различные термины для обозначения таких совокупностей: система, блок, серия, семья, цепочки, цикл и т.д. Мы будем использовать термин «система задач». Под системой задач будем понимать совокупность объектов, взаимодействие которых «вызывает» появление новых, интегративных качеств, не свойственным отдельно взятым образующим систему компонентов (Г.И.Саранцев, Ю.М. Колягин, О.Б.Епишева и др.)

Один из вопросов, который волнует учителя математики при подготовке к уроку – составление системы задач, которые он должен подобрать и включить в урок на каждом из этапов усвоения знаний учащимися.

Различные теории обучения по-разному рассматривают сущность и основные этапы усвоения. Наиболее распространенный подход раскрыт в работах С.Л. Рубенштейна, в соответствии с которыми усвоение предстает как процесс, включающий в себя четыре этапа.

1. Восприятие учебного материала на основе восприятия объектов, предметов, явлений, процессов с помощью наглядного образа или апперцепции; выделение этого объекта из фона и определение его свойств. Результатом данного этапа усвоения является формирование у обучающихся представлений об объекте, явлении и т.д.
2. Осмысление учебного материала путем раскрытия предметного содержания знания в его глубоких и многосторонних взаимосвязях - внутренних и внешних (с другими объектами и предметами). Результатом становится формирование понятий, установление причинно-следственных связей, законов и закономерностей, общих принципов устройства и функционирования определенных механизмов и т.д.
3. Запоминание учебного материала в результате многократного восприятия или повторения, воспроизведения существенных свойств и отношений. Организация данного этапа усвоения предполагает включение обучающихся в деятельность, в процессе которой происходит формирование стереотипных умений и навыков.
4. Применение изученного материала для решения практических задач, в процессе которого происходит овладение творческими способами деятельности. Организация данного этапа усвоения предполагает включение обучающихся в постепенно усложняющуюся деятельность по решению системы задач: перенос их в новую для обучающихся ситуацию, использование для решения новых задач.

Необходимо обратить внимание на достаточную условность выделения данных этапов, так как каждый этап усвоения частично включает в себя другой. Так осмысление начинается уже на этапе восприятия; запоминание (прочность усвоения) зависит от того, как организовано восприятие и осмысление, применение; наконец, все данные этапы могут носить более целостный и нерасторжимый характер в процессе решения проблемных задач, в которых применение, осмысление и запоминание слиты воедино.

Построенная на данной схеме усвоения теория учения В.В. Краевского и И.Я. Лернера обусловливает следующую логику работы учителя [2]:

1) создание условий для изучения обучающимися некоторого учебного материала, для его восприятия и осознания;

2) руководство процессом формирования у них способов применения знаний, т. е. формированием умений и навыков по образцу;

3) обеспечение творческого применения обучающимися ранее изученных знаний и умений.

В соответствии с вышесказанным, нами выделены три уровня усвоения школьниками математических знаний и способов действий:

- базовый (начальный), предназначенный для формирования обобщения базовых учебных элементов школьного курса математики основной школы, введения частички «нового» на основе использования единства понятий, знакомства с новым понятием на основе предыдущего обобщения и изучение его свойств;

- основной (фундаментальный), предназначенный для осуществления ближайшего видового обобщения, осмысления изученного материала: выполнения стандартных операций, применения знакомых методов для решения новых задач, знакомства с новыми методами;

- повышенный (творческий), предназначенный для применения обобщенных базовых учебных элементов школьной математики в жизни и нестандартных ситуациях, включает в себя широкое использование внутрипредметных связей [1].

Как известно, в учебниках по математике к каждой теме предлагается набор задач. Однако далеко не всегда этот набор и порядок расположения отвечают выделенным выше этапам работы учителя и соответствующим уровням усвоения школьниками математических знаний. Поэтому возникает необходимость в создании системы задач, которые соответствовали бы трем уровням усвоения знаний и последовательности действий учителя.

Задачи, соответствующие первому уровню усвоения математических знаний, должны основываться на использовании качества узнавания, воспроизведения и интерпретации учащимися изученного учебного материала. Например, найдите область определения функции ; найдите множество значений функции ; решите уравнение  и т.д.

Задачи второго уровня проверяют умение учащегося решать типовые задачи. Типовой задачей считается такая задача, условия которой допускают непосредственное применение усвоенных алгоритмов, правил или формул для ее разрешения. Например, укажите наименьшее значение функции ; определите, при каких значениях х график функции  лежит ниже графика функции y=5.

Задачи третьего уровня – это задачи, требующие от учащегося преобразования исходных условий и, часто, поиска дополнительных данных для подведения задачи под типовой алгоритм, а также нетиповые задачи, требующие от учащегося эвристической деятельности. Например, найдите сумму целых значений функции ; найдите разность между наибольшим и наименьшим значениями функции  на отрезке ; решите уравнение: .

Формируя систему задач к изучению любой темы, учитель должен включить задачи всех трех уровней.

Задачи первого уровня встречаются в учебниках. Но даже если их, по мнению учителя, недостаточно, то составить такие задачи самому не представляет труда.

Остановимся на задачах второго уровня, так как, по нашему мнению, второй уровень усвоения знаний школьниками очень важен. Без достижения этого уровня усвоения знаний о решении творческих задач не может быть и речи. Проанализировав задачи из современных учебников по алгебре и методических пособий, мы убедились, что в основном предлагается подборка задач либо первого уровня, либо третьего. Поэтому большую трудность для учителя представляет составление системы задач второго уровня.

Приведем примеры задач системы по теме «Логарифмическая функция», предназначенные для использования на втором уровне усвоения математических знаний школьниками.

Задача 1. Найдите область определения функции: .

В этой задаче учащиеся сталкиваются со знакомым заданием – нахождением области определения функции. Однако для его выполнения необходимо использовать не только знание свойств логарифмической функции, но и умение применять ранее полученные знания для решения задач. Здесь необходимо учитывать не только область определения логарифма, но и условие существование дроби. Таким образом старшеклассники получают подтверждение того факта, что и при участии нового объекта (логарифмической функции) для выполнения данного задания требуется решить смешанную систему, что они уже умеют делать.

Задача 2. Определите четность (нечетность) функций:

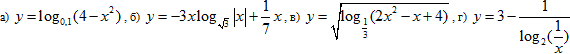
Стандартная по своей формулировке и алгоритму выполнения задача – определить четность функции. Учащиеся знают алгоритм:

1) найти область определения функции;

2) если область определения не симметрична относительно нуля, то делаем вывод, что функция не является четной и не является нечетной (функция общего вида); если область определения симметрична относительно нуля, то необходимо проверить равенства. Если  для любого  х  из области определения функции, то функция четная; если , то функция нечетная; функции, не принадлежащие ни одной из категорий выше, называются не чётными и не нечётными (или функциями общего вида).

Учащимся не составляет труда выполнить эту задачу по алгоритму, но при этом необходимо знать область определения элементарных функций и, как минимум, уметь решать неравенства и выполнять простейшие преобразования выражений. В задании а) необходимо решить неравенство  и использовать свойство квадрата числа, в задании б) – свойства модуля и преобразования буквенных выражений, в задании в) – достаточно решить неравенство , в задании г) –решить смешанную систему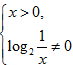 

Задача 3. Найдите множество значений функции:

а)

И в этой задаче задание знакомо старшеклассникам. Однако оно осложнено тем, что сама логарифмическая функция неограничена на области своего определения. Поэтому для выполнения задачи необходимо использовать не только свойства новой функции, но и рассматривать их во взаимосвязи с уже изученными функциями и их свойствами. Так, в задании а) необходимо убедиться, что свойства модуля не влияют на изменение множества значений логарифмической функции, но приходится учитывать свойства функции . В задании б) учащиеся убеждаются, что свойства функции  влияют на изменение свойств рассматриваемой логарифмической функции, а также на множество ее значений накладывает отпечаток и знак «минус», стоящий перед логарифмом. В задании в) необходимо использовать уже не только свойства квадратичной функции, но и учитывать еще одно свойство логарифмической функции – область определения. А в задании г) старшеклассникам предстоит связать между собой свойства уже трех функций: показательной, логарифмической и квадратичной. Таким образом, учащимся демонстрируется, с одной стороны, типичность самих заданий, а с другой стороны, – тесная взаимосвязь между математическими объектами, которые изучаются, казалось бы, вне связи друг с другом.

Обратим внимание на то, что в системе задач для второго уровня мы подобрали задания, которые отличаются от заданий начального (базового) уровня, но содержат в себе знакомые типы задач, позволяющие осуществить ближайшее видовое обобщение, выполнение стандартных операций, применение знакомых методов для решения новых задач; кроме того, они формируют общелогические и специфические умения, которые используются далее при решении задач следующего уровня. Использование такой подборки позволяет школьникам эффективно усваивать новые математические знания и обобщать знания за предыдущие периоды.

Литература

1. Аммосова Н.В., Краснова Г.Г. Конструирование курса «Алгебра и начала анализа» в старших классах общеобразовательной школы с учетом принципов систематизации и преемственности / Вестник Поморского университета. Серия «Гуманитарные и социальные науки». – 2011. – № 8.– С. 196-201.
2. Лернер И. Я. Качества знаний учащихся. Какими они должны быть? – М.: Знания, 1978. – 112 с.

References

1. Ammosova N.V., Krasnova G.G. Konstruirovanie kursa «Algebra i nachala analiza» v starshih klassah obshheobrazovatel'noj shkoly s uchetom principov sistematizacii i preemstvennosti / Vestnik Pomorskogo universiteta. Serija «Gumanitarnye i social'nye nauki». – 2011. – № 8.– S. 196-201
2. Lerner I. Ja. Kachestva znanij uchashhihsja. Kakimi oni dolzhny byt'? – M.: Znanija, 1978. – 112 s.