ТЕСТОВЫЕ МЕТОДЫ ДИАГНОСТИРОВАНИЯ ПРИБОРОВ УЧЕТА РАСХОДА ТЕПЛОНОСИТЕЛЯ

Виноградов А.Н.¹, Чипулис В.П.²

¹Кандидат технических наук; ²доктор технических наук, профессор, Институт автоматики и процессов управления ДВО РАН

ТЕСТОВЫЕ МЕТОДЫ ДИАГНОСТИРОВАНИЯ ПРИБОРОВ УЧЕТА РАСХОДА ТЕПЛОНОСИТЕЛЯ

Аннотация

Работа посвящена подходу к диагностированию технического состояния приборов для измерения расхода применяемых на одном из наиболее представительных классов объектов теплоэнергетики – закрытых системах теплопотребления, то есть таких систем, из которых не осуществляется (в исправном техническом состоянии) водозабор для нужд горячего водоснабжения. В качестве дефектов рассматриваются наиболее часто встречающиеся на практике –  утечки (или подпитки, то есть утечки со знаком минус) и инструментальные погрешности измерений, превышающие допустимые значения. Предложен метод решения задачи, результатом которого являются не только конкретные значения диагностируемых величин утечки и погрешностей, но и области так называемых рабочих решений.

Ключевые слова: теплоэнергетика, диагностика приборов, учет тепловой энергии, расходомер.

Vinogradov A.N.¹, Chipulis V.P.²

¹Candidate of Engineering Sciences; ²Doctor of Engineering Sciences, professor, Institute of Automation and Control Processes FEB RAS

TEST METHODS OF DIAGNOSIS OF DEVICES OF THE ACCOUNT OF FLOW OF HEAT CARRIER

Abstract

The work is devoted to approach to technical state diagnostics of devices for measurement of flow rate applied on one of the most representative classes of objects of power - closed systems of heat, that is such systems, of which not done (in good technical condition) withdrawals for hot water supply. As defects are considered most commonly encountered - leak (or recharge, i.e. leakage with a minus sign and instrument errors of measurements exceeding the acceptable value. The method of solving the task, the result of which are not only specific values diagnosed quantities leak and mistakes, but also the field of the so-called working solution.

Keywords: thermal power engineering, diagnostics devices, metering of heat energy, flowmeter.

При диагностировании объектов могут использоваться как функциональные, так и тестовые методы диагностирования [1]. В теплоэнергетике, безусловно, предпочтительнее использовать функциональные методы, реализация которых проходит в процессе функционирования объекта, т.е. в эксплуатационном режиме, прерывать который, особенно в течение отопительного сезона, весьма нежелательно. Однако во многих случаях добиться удовлетворительных результатов, т.е. достаточно точно локализовать дефект, не удается с использованием методов функционального диагностирования. При этом практически неизбежной становится организация специальных тестовых режимов работы объекта, т.е. переход к тестовым методам.

При диагностировании измерительных приборов установленных на теплоэнергетических объектах (ОТЭ) для учета и контроля параметров теплоносителя могут использоваться как функциональные, так и тестовые методы диагностирования. В теплоэнергетике, безусловно, предпочтительнее использовать функциональные методы. Но реализация данных методов проходит в процессе функционирования объекта, т.е. в эксплуатационном режиме, прерывать который, особенно в течение отопительного сезона, весьма нежелательно. Однако во многих случаях добиться удовлетворительных результатов, т.е. достаточно точно локализовать дефект, не удается с использованием методов функциональной диагностики. При этом практически неизбежной становится организация специальных тестовых режимов работы объекта, т.е. осуществляется переход к тестовым методам диагностирования.

Поэтапная технология диагностирования измерительных приборов.

Измерительные приборы, применяемые на объектах теплоэнергетики, позволяют охарактеризовать работу объекта в каждый момент времени определенной совокупностью измеренных значений параметров теплоносителя в трубопроводах тепловой сети. Понятно, что эти параметры взаимозависимы и не могут изменяться во времени произвольно. Все основные, базовые зависимости между параметрами отражены в проектной документации. Однако использовать эти зависимости при решении задач анализа режимов функционирования и управления зачастую нельзя в силу  их неадекватности реальным объектам по различным причинам (отклонение от проекта при строительстве, устаревание объекта без надлежащих мероприятий по поддержке его технического состояния). При этом, по сути, единственным источником информации об объекте (его моделью) являются результаты измерений параметров, анализируя которые можно выявить реальные зависимости между параметрами и вовлекать их в дальнейшем в процесс решения конкретных задач. Другой существенной причиной несоответствия закономерностей изменения параметров закономерностям правильной работы объекта могут быть физические дефекты. Примерами физических дефектов являются утечки в трубопроводах, дефекты вентилей (например, вентиль не позволяет осуществлять перекрытие канала транспортируемой среды), метрологический отказ (погрешность измерительного прибора превышает указанную в его паспорте величину), катастрофические дефекты измерительного оборудования, ассоциируемые с кодами ошибок, индицируемых встроенными средствами контроля.

На первом этапе диагностирования по сути выявляются те или иные нештатные или критические ситуации, приводящие к нарушениям (отклонениям от нормы) в поведении тепловых систем. Причины возникновения некоторых из них могут быть очевидны, так же как и пути их устранения. Однако в общем случае возникновение нештатной или критической ситуации может вызываться несколькими причинами, действующими одновременно. Очевидно, что при этом задача усложняется (по аналогии с задачей диагностирования кратных неисправностей). В данной статье ограничимся рассмотрением систем теплопотребления (тепловых узлов потребителей тепловой энергии, ИТП).

Диагностирование измерительных приборов в закрытых системах теплопотребления

Рассмотрим закрытую систему теплопотребления, под которой понимается система, из которой не осуществляется (в исправном ее техническом состоянии) водоразбор для нужд горячего водоснабжения. На Рис. 1а) схематично представлена закрытая система теплопотребления.

Заметим, что нам не известны истинные значения расходов в подающем и обратном трубопроводах М_под и М_обр, а известны лишь их измеренные значения расходомерами 1 и 2 (М¹_под и М²_обр). Очевидно, что в системе должен соблюдаться баланс потоков теплоносителя. Условие соблюдения баланса согласно требованиям нормативной базы (как при коммерческих, так и технологических измерениях) выглядит следующим образом:

1. │ M¹_под – M²_обр│ ‌≤ 0,01r(M¹_под + M²_обр),

где r – допустимая относительная погрешность измерения расхода, в частности требования НБ [2] не более ±2%.

Нарушение баланса (превышение разности расходов допустимой величины) может объясняться различными причинами. Наиболее вероятные из них две. (Возможны и другие, но они встречаются на практике чрезвычайно редко). Первая – утечка (подпитка) в системе теплопотребления. Вторая – погрешность  измерений расхода. Очевидно, что обе эти причины – утечка и погрешность измерений, могут присутствовать одновременно. В этом случае важно знать долю каждого из этих факторов в величине рассогласования расходов.

Далее будем полагать, что причиной рассогласования расходов является либо утечка, либо метрологический отказ измерителей расхода, либо оба эти дефекта одновременно.

Метрологический отказ – превышение относительной погрешности прибора максимально допустимого значения. В дальнейшем будем пользоваться термином погрешность, имея в виду при этом относительную инструментальную погрешность расходомера.

Вначале примем, предположение о том, что величина утечки не меняется и расход теплоносителя поддерживается постоянным в периоды измерений, результаты которых используются при диагностировании измерительных приборов.

Погрешность измерений обусловливается многими факторами. Наиболее существенным из них, во многом определяющим точность результата измерений, является инструментальная погрешность – погрешность средств измерений. Сформулируем задачу диагностирования технического состояния измерительного прибора на примере, когда выявлено превышение величины дисбаланса потоков закрытой системы. В паспорте на средства измерений, а также в нормативных документах указывается относительная погрешность измерительного прибора. Под относительной погрешностью понимается величина:

2. Δ = ( х_и – х_д) / х_д ,

где х_и - показание прибора, х_д  - действительное значение измеряемой величины. Относительная погрешность выражается либо в долях (∆), либо в процентах (δ =100∆%). В дальнейшем будем пользоваться термином погрешность, имея в виду при этом относительную инструментальную погрешность расходомера.

Из (2) имеем:

3. x_и=x_д(1+Δ) или x_и=x_д(1+0,01δ).

Вернемся к рассмотрению схемы Рис. 1а). Положим, что величина рассогласования результатов измерений расхода в прямом и обратном трубопроводах превышает допустимое значение. Для определения причин этого рассогласования проводиться следующий тест. Меняются расходомеры 1 и 2 местами (Рис. 1б)), обеспечивая при этом неизменность всех прочих условий измерений, главное из которых - сохранение значений расходов в прямом и обратном трубопроводах. Если после такой замены картина не изменится, т.е. M1под - M2обр = M2под – M1обр, то, очевидно, что причина не в погрешностях расходомеров, а в утечке (подпитке). Если же в результате измерений согласно схеме Рис 1б)

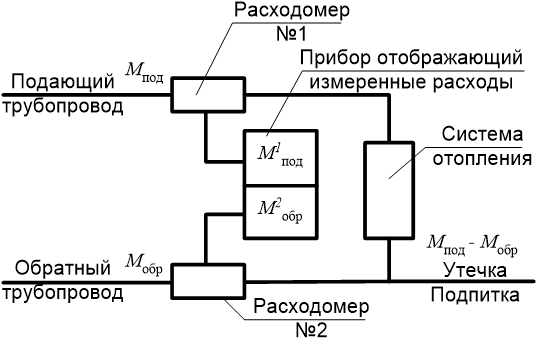
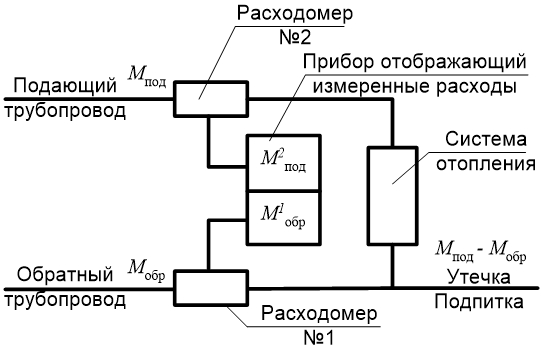
Рис. 1

получим обратный (по знаку величины рассогласования) результат, то есть M_1под - M_2обр = - (M_2под - M_1обр), то рассогласование объясняется погрешностями приборов. Однако наиболее вероятны не эти крайние случаи, а другие, определяемые соотношениями:

4. M¹_под - M²_обр ¹ M²_под  - M¹_обр,  M²_под  - M¹_обр  ¹ - (M²_под  - M¹_обр)

Соответствующие (4) рассогласования результатов измерений вызываются совместным влиянием (наличием) утечки и погрешностей расходомеров. На практике, как было отмечено ранее, важно знать количественные характеристики этих величин.

Введем для упрощения формульного представления результатов измерений следующие обозначения:

M¹_под= а, M²_обр= b, M²_под = с, M = d; Δ₁ (Δ₂) – погрешности расходомеров 1 (2) в долях; δ₁ (δ₂) – погрешности расходомеров 1 (2) в процентах; k₁=1+Δ₁, k₂=1+Δ_2.. Величины k₁ и k₂ назовем коэффициентами погрешностей расходомеров 1 и 2. Далее, абстрагируясь от содержательной стороны дела, сформулируем формальную постановку задачи диагностирования.

Дана система четырех уравнений с четырьмя неизвестными.

5. 

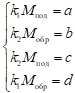
Необходимо определить количественные характеристики неизвестных системы.

Получение решения для абсолютных показателей работы тепловых систем

Получим решение задачи для области абсолютных показателей функционирования тепловой системы.

Положим для примера, что а = 120, b = 85, с = 102, d = 100. (Единицы измерений расхода для простоты опускаются в предположении, что они одинаковы для всех результатов измерений). С учетом этого система (5) примет вид:

6. 

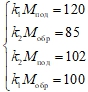
Система (6) имеет бесконечное множество решений. Очевидно, что далеко не все из них могут быть приняты в качестве «рабочих», основываясь на которых, можно было бы предпринять конкретные действия по нормализации ситуации – поверке расходомеров и/или поиску места утечки. Прежде чем более определенно говорить о реальности частных решений системы (6), положим для рассматриваемого примера, что максимальный допустимый расход сетевой воды (а это ограничение всегда имеет место для конкретного теплового узла) равен 150, а динамический диапазон измерений расходомеров (диапазон, в котором обеспечивается требуемая точность измерений) равен [5¸200].

Рассмотрим два из теоретически возможных решений. Первое из них следующее:

М_под = 1200;

М_обр = 1000;

k₁ = 0,1 (Δ₁ = −0,9; δ₁ = −90%);

k₂ = 0,085 (Δ₂ =−0,915; δ₂ = −91,5%).

Данное решение следует признать «нерабочим», поскольку величина расхода значительно превышает допустимую. О погрешностях расходомеров в данном случае ничего определенного сказать нельзя, так как даже если допустить возможность таких величин расходов, то расходомеры работают явно вне диапазона, в пределах которого обеспечивается требуемая точность измерений.

Второй теоретически возможный вариант решения системы (6):

М_под = 10;

М_обр = 8,5;

k₁ = 12  при (Δ₁ = 11; δ₁ = 1100%);

k₂ = 10 при (Δ₂ = 9; δ₂ = 900%).

Величины расходов в примере правдоподобны, измерения производятся в рабочем диапазоне. Однако погрешности расходомеров порядка 1000% следует признать практически невероятными. Дело в том, что метрологический отказ, который в данном случае мы имеем в виду и который приводит к превышению допустимой погрешности, связывается с постепенным ухудшением точностных характеристик измерительных приборов. А дефекты катастрофического типа, приводящие к резкому искажению результатов измерений, в современных измерительных приборах выявляются встроенными средствами диагностирования.

Для сужения множества решений системы (6) с целью перехода к области «рабочих» поступим следующим образом. Примем допущение о том, что относительная погрешность каждого расходомера не может превышать (по модулю) 20%. Заметим, однако, что уровень 20% без потери общности может быть изменен в случае необходимости.

Исходя из принятого допущения, построим зависимости – графические и аналитические, связывающие значения из области «рабочих» решений системы (6) и позволяющие определить интервалы допустимых значений переменных системы.

Обозначим .

Величина k легко определяется из (6) путем деления уравнения 2 на уравнение 4 (или 3 на уравнение 1): .

Далее имеем: 

Умножив обе части последнего уравнения на 100, получим уравнение, связывающее значение относительных погрешностей (в процентах) расходомеров:

7. δ₂ = 100(k–1)+kδ₁.

Сопоставим оси абсцисс погрешность δ₁ , оси ординат - δ₂ и ограничим пространство прямыми δ₁=20%, δ₂=20% , δ₁= -20%, δ₂= -20%, что соответствует принятому ограничению относительно соответствующих “рабочим” решениям значений погрешностей расходомеров. На Рис. 2 приведена номограмма, отражающая графики прямых, соответствующие уравнению (7) для различных значений k и вписанные в область рабочих решений.

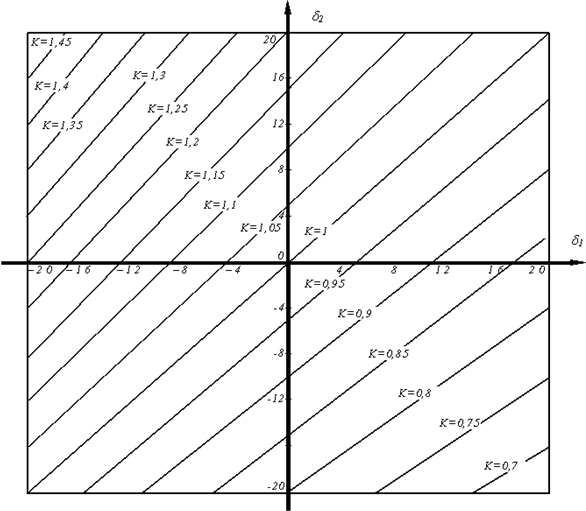
Рис. 2

Обратимся снова к системе уравнений (6) с реальными значениями величин расхода. Из (6) имеем .

Уравнение (7) с учетом конкретного значения k примет следующий вид:

8. δ₂= -15+ 0,85 δ₁

Из номограммы (график для k=0,85), либо путем несложного анализа уравнения (8) (с учетом ограничения на величину погрешностей) определим интервалы возможных значений δ₁ и δ₂.

9. 

Заметим, что не любые значения δ₁ и δ₂, удовлетворяющие условиям (9), являются решением системы (6), а лишь те из них, которые связаны уравнением (8) и представлены графиком прямой для k=0,85 Рис. 2. Далее определим интервал возможных значений М_под и М_обр и как следствие интервал значений утечки М_y=М_под - М_обр.

Разделив обе части уравнения 1 на уравнение 4 системы (6), получим

10. 

Минимальные и максимальные значения М_под из области рабочих решений могут быть получены, например, из уравнения 1 системы (6) с учетом интервала значений δ₁.

М_под min = 100

М_под max =127,5

Соответственно

М_обр min =83,3

М_обр max =105,8

По точкам с координатами (М_под min, М_обр min) и (М_под max, М_обр max) построим график уравнения (10), отражающий возможные значения расходов М_под и М_обр  (Рис. 3).

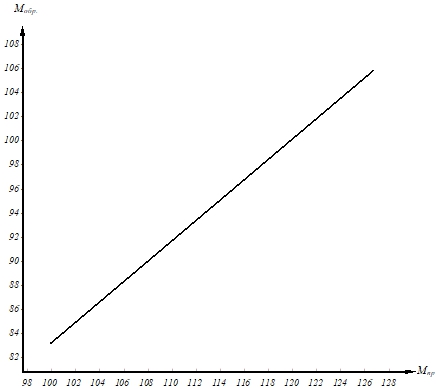
Рис. 3 - Очевидно, что величина утечки находится в следующих пределах:17,7 £ М_y £ 21,7

Отметим следующее важное обстоятельство, непосредственно связанное с достоверностью заключений, получаемых на первом этапе диагностирования – этапе оперативного наблюдения за функционированием тепловой системы с целью определения соответствия предъявляемым к ней требованиям.

Предположим для рассмотренного выше примера, что первоначально расходомеры (с теми же значениями погрешностей) установлены по варианту 2, т.е. переставлены местами изначально. Тогда при проверке баланса расходов мы бы получили в результате измерений рассогласование, равное 2 (102 - 100 = 2). Это меньше 2% от (М_под + М_обр), т.е. нормативное требование [2] выполнено. На практике при этом негласно подразумевается, что величина утечки и погрешности расходомеров находятся в пределах допустимых величин. Однако это несправедливо, о чем свидетельствуют результаты измерений по варианту 1 (первоначальное расположение расходомеров).

Следовательно, достоверную картину можно получить, лишь проведя дополнительные мероприятия либо по поверке расходомеров, либо, например, по созданию специальных тестовых режимов, позволяющих определить утечку (или установить ее отсутствие). На практике, естественно, такие мероприятия не проводятся, так как не регламентируются существующей нормативной базой. Единственное, что делается в направлении повышения достоверности результатов измерений – обязательная поверка расходомеров через определенный период времени (межповерочный период), который указывается в паспорте на средство измерения. Однако опыт показывает, что погрешности расходомеров выходят за пределы допустимых величин гораздо раньше, чем истекает межповерочный период.

Получение решения для относительных показателей работы тепловых систем

Система уравнений (5), как было отмечено выше, имеет бесконечное множество решений, если в качестве искомых величин рассматривать переменные M_под, M_обр, k₁ и k₂. С учетом этого выше был описан метод определения не конкретных значений переменных, а интервалов, в которых они находятся, в предположении, что погрешность каждого из измерительных приборов не превышает определенной величины, выбираемой из практических соображений. Однако получаемые при этом «интервальные» решения нельзя признать удобными для дальнейшего использования. Более того, на практике первоочередной интерес представляют не значения погрешностей приборов измерения расходов (которые принципиально могут быть получены лишь при поверке расходомеров с использованием проливочного стенда), а то, насколько они рассогласованы, то есть насколько расходятся их показания при измерении одинаковых величин. То же можно сказать и о расходах M_под, M_обр. Интерес представляют в основном не конкретные значения расходов в подающем и обратном трубопроводах системы и даже не конкретное значение их разности (утечки), а относительная разность расходов, то есть относительная утечка, показывающая, насколько велики относительные потери теплоносителя в системе. С учетом этого модифицируем постановку задачи и в качестве искомых величин при решении системы уравнений (5) примем относительную утечку δ_M и относительную разность коэффициентов погрешностей δ_k расходомеров 1 и 2:

11. δ_M (%) = 100( M_под - M_обр) / 0,5(M_под + M_обр), 12. δ_k (%) = 100(k₁ - k₂) / 0,5(k₁ + k₂)

Получим в общем виде выражение для определения значения относительной утечки d_M, исходя из результатов измерения расходов до и после перестановки расходомеров. Для этого разделим числитель и знаменатель правой части выражения (11) на M_под:

13. δ_M (%) = 100(1 - M_обр ‌/ M_под) / 0,5(1 + M_обр‌ / M_под),

Далее, обратившись к паре уравнений 4 и 1 (и разделив левую часть уравнения 4 на левую часть уравнения 1 и правую часть уравнения 4 на правую часть уравнения 1), а так же 2 и 3 системы уравнений (5), получим:

14. M_обр/ M_под = d / a = b / c Подставив в (13) вместо M_обр / M_под  значения d / a или b / c из (14), имеем: 15. δ_M (%) = 100 (1 - d / a) / 0,5(1 + d / a) = 100 (a - d) / 0,5(a + d) или 16. δ_M (%) = 100 (1 - c / b) / 0,5(1 + c / b) = 100 (c - b) / 0,5(c + b)

Выражения (15) и (16) позволяют определить, в отличие от метода, описанного выше, не интервальное, а конкретное решение, а именно, конкретное значение относительной погрешности системы. Аналогичным образом могут быть получены выражения для вычисления относительной разности коэффициентов погрешностей:

17. δ_k (%) = 100(a - c) / 0,5(a + c) 18. δ_k (%) = 100(d - b) / 0,5(d + b)

Вычислим значение δ_M и δ_k для примера, взятого из вышеописанного раздела. Напомним, что а = 120, b = 85, с = 102, d = 100. (Единицы измерений расхода для простоты опускаются, хотя, естественно, предполагается, что они одинаковы для всех результатов измерений). С учетом этого система примет вид (6).

Из выражения (15) определим значение относительной утечки:

δ_M (%) = 100 (120 - 100) / 0,5(120 + 100) ≈ 18,2%

Нетрудно убедиться, что с использованием выражения (16) будет получено то же решение.

С использованием выражения (17) получим значение относительной разности коэффициентов погрешностей расходомеров: δ_k (%) = 100(120 - 102) / 0,5(120 + 102) ≈ 16,2%

Литература

1. KuznetsovR., ChipulisV.. Regression Analysis in Energy Systems // Advanced Materials Research. Materials, MechatronicsandAutomationII. Vol. 740, 2013. P. 772-777
2. Правила коммерческого учета тепловой энергии, теплоносителя, утверждены постановлением Российской Федерации от 18.11.2013г. №1034.