СЦЕНАРИИ ПЕРЕХОДА НЕЛИНЕЙНЫХ КОЛЕБАНИЙ ИЗ ГАРМОНИЧЕСКИХ В ХАОТИЧЕСКИЕ ДЛЯ БАЛОК ТИПА ТИМОШЕНКО
Крысько В.А.1, Папкова И.В.2, Жигалов М.В.3, Салтыкова О.А.4, Шелудько Н.А.5
1Доктор технических наук, профессор, 2кандидат физико-математических наук, доцент, 3доктор физико-математических наук, 4кандидат физико-математических наук, PhD, доцент, 5студент, Саратовский государственный технический университет имени Гагарина Ю.А.
РФФИ Грант МОЛ
СЦЕНАРИИ ПЕРЕХОДА НЕЛИНЕЙНЫХ КОЛЕБАНИЙ ИЗ ГАРМОНИЧЕСКИХ В ХАОТИЧЕСКИЕ ДЛЯ БАЛОК ТИПА ТИМОШЕНКО
Аннотация
В данной работе рассматривается однослойная балка, находящая под действием локальной знакопеременной нагрузки с учетом геометрической нелинейности. Построенная математическая модель основывается на гипотезах С.П.Тимошенко. Переход от гармонических колебаний к хаосу происходит по сценарию Рюэля-Такенса-Ньюхауза.
Ключевые слова: балка типа Тимошенко, сценарии перехода в хаос, фурье-анализ.
Krys'ko VA1, Papkova I.V.2, Zhigalov M.V.3, Saltykovа O.A.4, Shelud'ko N.A.5
1Dr. in Engineering, 2PhD in physical and mathematical sciences, 3Dr. in physical and mathematical sciences, 4PhD in physical and mathematical sciences, 5Student Yuri Gagarin State Technical University of Saratov
SCENARIOS OF TRANSITION FROM HARMONIC NONLINEAR OSCILLATIONS IN CHAOTIC BEAMS TIMOSHENKO TYPE
Abstract
In this paper we consider a single-layer beam under the influence of the local oscillating loads, taking into account the geometric nonlinearity. Constructed a mathematical model based on hypotheses SPTimoshenko. Transition from harmonic oscillations to chaos scenario occurs Ruelle-Takens-Newhouse.
Keywords: beam of Timoshenko type, transition scenarios in chaos, Fourier analysis.
Постановка задачи
Рассматривается гибкая однослойная балка. Она нагружается распределенной на краю нагрузкой ![]() . Для модели С.П. Тимошенко приняты следующие гипотезы:
. Для модели С.П. Тимошенко приняты следующие гипотезы:
1) размер балки по оси OX гораздо больше ее поперечных размеров;
2) ось балки представляет собой прямую линию;
3) сечения, расположенные вдоль балки, изгибаются независимо и не влияют друг на друга (таким образом, напряжения, нормальные к площадкам, которые параллельны оси, достаточно малы и ими можно пренебречь);
4) обозначим за ![]() , смещения точек срединной линии
, смещения точек срединной линии ![]() – смещения произвольных точек балки.
– смещения произвольных точек балки.
5) тангенциальные перемещения ![]() , распределены по толщине
, распределены по толщине ![]() по линейному закону [1];
по линейному закону [1];
6)Для описания связи между деформацией и перемещениями используется теория Т. фон Кармана [1].
Данная модель балки описывается системой нелинейных дифференциальных уравнений в частных производных. Для обеспечения общности исследования размерная система уравнений приводится в безразмерной форме [2]:
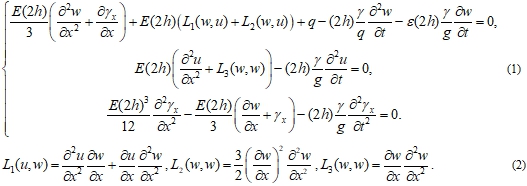
где ![]() – нелинейные операторы,
– нелинейные операторы, ![]() – прогиб элемента в направлении нормали;
– прогиб элемента в направлении нормали; ![]() – перемещение элемента в продольном направлении;
– перемещение элемента в продольном направлении; ![]() - угол поворота нормали к линии
- угол поворота нормали к линии ![]() ,
, ![]() – коэффициент диссипации;
– коэффициент диссипации; ![]() – модуль Юнга; h – высота поперечного сечения панели;
– модуль Юнга; h – высота поперечного сечения панели; ![]() – удельный вес материала;
– удельный вес материала; ![]() – ускорение свободного падения; t – время.
– ускорение свободного падения; t – время.
Для замыкания системы к дифференциальным уравнениям (1) присоединяем граничные условия и начальное условие.
Заделка – заделка:
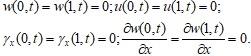 (3)
(3)
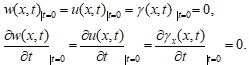 (4)
(4)
Система уравнений (1-4) сводится к системе обыкновенных дифференциальных уравнений с помощью метода конечных разностей, которая решается методом Рунге-Кутты четвертого порядка точности. Предварительно исследовался вопрос о выбора числа деления отрезка n по пространственной координате x ϵ [0; 1]. Исследования показали, что оптимальным числом деления отрезка n = 40. Шаг по времени выбирается по правилу Рунге.
Численный эксперимент
Рассматриваем прямолинейную балку с однородными граничными условиями (3) и нулевыми начальными условиями (4), находящейся под действием знакопеременной, равномерно распределенной нагрузки, заданной в виде ![]() , где
, где ![]() . Коэффициент диссипации
. Коэффициент диссипации ![]() . Целью работы является изучение сценариев перехода из гармонических в хаотически колебаний балок, находящиеся по действием локальной нагрузки, действующей на четверть балки к ее левому краю.
. Целью работы является изучение сценариев перехода из гармонических в хаотически колебаний балок, находящиеся по действием локальной нагрузки, действующей на четверть балки к ее левому краю.
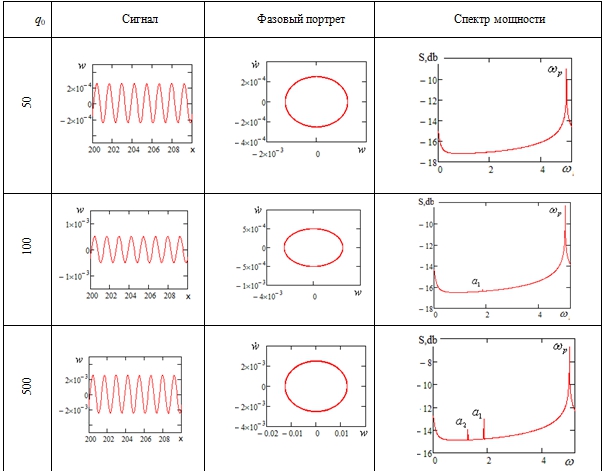
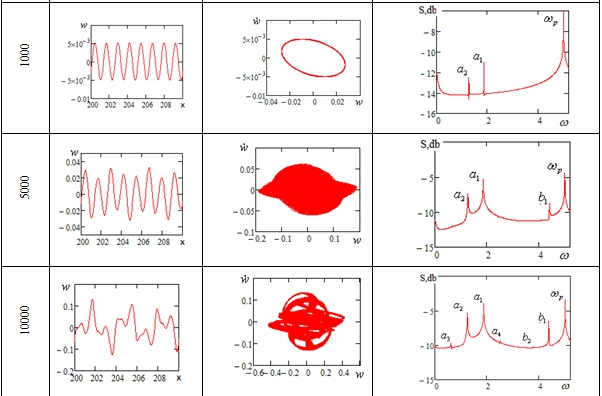
- Колебания совершаются на основной частоте возбуждения
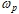 и являются гармоническими (
и являются гармоническими (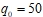 ).
). - Далее, увеличивая амплитуду нагрузки до
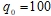 , наблюдаем в спектре мощности возникновение линейно независимой частоты колебаний
, наблюдаем в спектре мощности возникновение линейно независимой частоты колебаний 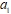 . Система переходит в состояние двухчастотных колебаний на частотах
. Система переходит в состояние двухчастотных колебаний на частотах 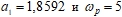 .
. - При увеличении нагрузки до
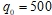 , происходит образование линейно-зависимой от
, происходит образование линейно-зависимой от 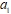 частоты
частоты 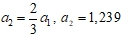
- При нагрузке
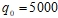 мы видим образование линейно-зависимой частоты
мы видим образование линейно-зависимой частоты 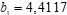 . Причем
. Причем 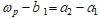 . Фазовый портрет становится предельным циклом.
. Фазовый портрет становится предельным циклом. - Дальнейшее движение по амплитуде нагрузки приводит к образованию новых линейно-зависимых частот колебаний
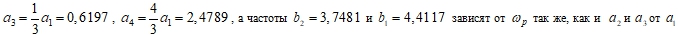 . Сигнал и фазовый портрет становятся хаотическими.
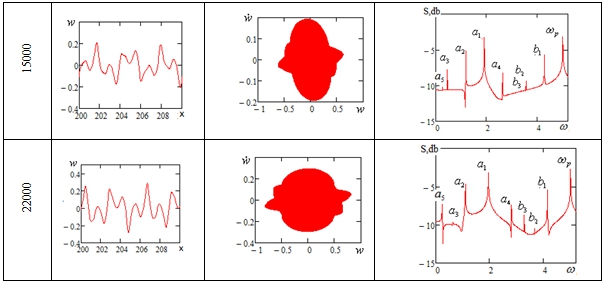
. Сигнал и фазовый портрет становятся хаотическими. - Затем при увеличении нагрузки до
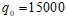 возникает новая комбинация линейной зависимости:
возникает новая комбинация линейной зависимости: 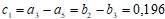 .
. - Таким образом, серия возникновения зависимых частот колебаний приводит систему в состояние хаоса на частоте возбуждения (
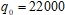 ).
).
Следовательно, переход в хаос осуществляется по сценарию Рюэля-Такенса-Ньюхауза, т.е. появляется новая линейно независимая частота и переход к хаосу происходит через серию линейных комбинаций линейно-зависимых частот.
Литература
- Вольмир А.С. Нелинейная динамика пластинок и оболочек / А.С. Вольмир.- М.: Наука, 1972.- 492 с.
- А. В. Крысько, М. В.ЖигаловМатематические модели и методы исследования сложных колебаний неклассических распределенных механических систем; Сарат. гос. техн. ун-т (Саратов). - Саратов : СГТУ, 2008. - 230 с.
- Григолюк Э.И. Неклассические теории колебаний стержней, пластин и оболочек / Э.И. Григолюк, И.Т. Селезов // Механика твердых деформируемых тел. Т. 5. М.: ВИНИТИ, 1973.- 272 с.
