РАЗНОСТНО – КОРРЕЛЯЦИОННЫЙ МЕТОД ИЗМЕРЕНИЯ ДВИЖЕНИЯ ИЗОБРАЖЕНИЯ

Лазарев Н.Ю.

Аспирант, Самарский государственный технический университет

РАЗНОСТНО – КОРРЕЛЯЦИОННЫЙ МЕТОД ИЗМЕРЕНИЯ ДВИЖЕНИЯ ИЗОБРАЖЕНИЯ

Аннотация

В статье представлены результаты компьютерного моделирования автокорреляционных и взаимно корреляционных функций разностных изображений видеоряда движущейся сцены и оценки их использования для измерения вектора скорости движения.

Ключевые слова: разностное изображение, вектор скорости, корреляционная функция.

Lazarev N.Y.

Postgraduate student, Samara State Technical Univetsity

RAZNOSTNO – THE CORRELATION METHOD OF MEASUREMENT OF MOVEMENT OF THE IMAGE

Abstract

Results of computer modeling of autocorrelated and mutually correlation functions of differential images of a video series of a moving scene and assessment of their use are presented in article for measurement of a vector of speed of movement.

Keywords: differential image, speed vector, correlation function.

Движение является одним из главных факторов анализа динамических сцен. Не случайно биологические зрительные сенсоры используют движение для выделения интересующих их объектов из фона. Например, лягушки реагируют только на движущихся насекомых. Некоторые устройства технического зрения работают по такому же принципу. Известны видеорегистраторы, включающие автоматическую запись видеосигнала только при наличии динамической составляющей на контролируемом объекте. При этом важен факт самого движения, а не изменения освещенности или других параметров изображения.

Появление новых стандартов видеокодирования, таких как H.264 и MPEG-4, основано на широком использовании векторов движения динамических блоков изображения, остающихся практически неизменными на протяжении ряда кадров [1]. Закодированная информация о таком блоке на начальном кадре используется далее путем переноса на следующих кадрах. Не менее важна задача автоматической стабилизации изображений на основе контроля смещений [2]. Другая важная задача – восстановление смазанных движением изображений методом деконволюции [5]. Для ее эффективного решения необходимо знать функцию рассеяния точки (ФРТ размытия), вычисляемую на основе параметров движения.

Большой класс задач, связанных с определением движения изображения, относится к управлению движением автономных роботов, автономной навигации беспилотных летательных и космических аппаратов [7-9].

В общем виде оценка движения локальных областей изображения и отдельных точек решается с помощью уравнения оптического потока [3]. Для условия неизменности освещенности сцены за время анализа это уравнение имеет вид:

где:  - пространственный градиент яркости в точке (x, y);  - вектор скорости оптического потока.

Если предположить, что в окрестности каждой точки изображения значение оптического потока одинаково, то можно записать основное уравнение оптического потока для всех пикселей окрестности и решить полученную систему для всех пикселей окрестности методом наименьших квадратов, как это сделано в алгоритме Лукаса - Канаде [4].

Использование локальных областей (блоков, эталонов) лежит в основе большого класса корреляционно-экстремальных систем (КЭС). Работа таких систем подробно рассмотрена в литературе [2, 8, 9] и здесь не анализируется. Отметим только, что КЭС не позволяют измерять скорость при движении, как в прямом, так и в обратном направлении. Для реализации такой функции требуется два коррелятора, один из которых работает в прямом, а другой – в обратном направлении [2].

Из всего перечисленного множества задач рассмотрим те из них, которые требуют оценки глобального движения, когда вектор движения элементов изображения одинаков для всех точек. Такая ситуация имеет место, когда достаточно удаленная сцена движется без вращения относительно неподвижной камеры или наоборот, камера движется относительно сцены.

Пусть видеокамера формирует последовательность кадров (фреймов) полутоновых черно-белых изображений движущейся сцены с межкадровым периодом и временем экспозиции . Примем в первом приближении, что освещенность сцены достаточна, τ мало, и смазом изображения за время экспозиции можно пренебречь. Тогда все элементы кадров, кроме краевых, сдвигаются на величину  , а скорость движения изображения равна

,      (1)

где N – число кадров, между которыми определяется сдвиг.

Отметим, что все параметры привязаны к изображениям: сдвиг измеряется в пикселях (пик), скорость – в пик/сек.

Один из наиболее простых и распространенных способов оценки межкадрового сдвига между фреймами  взятыми в моменты времени , основан на вычислении поэлементной разности соответствующих фреймов [7]. Такая разность вычисляется по формуле

   (2)

где Θ – значение порогового уровня.

Формула (2) позволяет формировать так называемые разностные изображения. Очевидно, если исходное изображение  содержит значительные однородные области, то разность яркостей элементов, принадлежащих этим областям, будет минимальной, меньше порога Θ. На разностном изображении  они принимают значение 0. Для областей с высоким градиентом (кромки, границы объектов) элементы в результате движения существенно отличаются по яркости, и они принимают значение 1. Таким образом, при формировании разностных изображений осуществляется своего рода двухуровневая сегментация (бинаризация) движущихся областей на изображении.

Результаты, представленные в данной публикации, получены путем компьютерного моделирования в среде MATLAB. На рис.1 показана последовательность трех полутоновых изображений f1, f2, f3 размером MxM (M=256) движущегося ландшафта.

Рис. 1 - Исходные изображения. Показана ось времени t и вектор скорости изображения

Предполагается, что наблюдатель с камерой находится на достаточно большом расстоянии от объектов ландшафта и все точки изображения движутся с одинаковой скоростью Vиз. В результате движения элементы соседних изображений сдвигаются на ∆ пикселей (на рисунке ∆ = 20) в направлении вектора движения.

На рисунке 2а представлены разностные изображения , полученные при Θ=50. Как видно из примера, разностные изображения содержат много единичных пикселей и мелких областей. Хотя для соседних фреймов существенная разница в шумовых компонентах маловероятна, тем не менее, мелкие градиентные детали проявляются существенно. Для их устранения применим морфологические операции [6]. Так, для устранения изолированных точек и мелких областей хороший эффект дает операция эрозии  со структурным элементом B. После эрозии целесообразно нарастить оставшиеся объекты с помощью операции дилатации:

Последовательное применение этих операций называется размыканием бинарного изображения . Его результат показан на рис. 2б. В качестве структурного элемента использован квадрат 5х5.

Рис. 2 - а) Разностные изображения    б) размыкание 

Исследуем корреляционные функции разностных изображений. Сформируем суммарное изображение  и двойное разностное  и определим их автокорреляционные функции (АКФ). Поскольку разностные изображения сильно коррелированны, справедливы следующие соотношения:

, где через ВКФ обозначена взаимно корреляционная функция. (3)

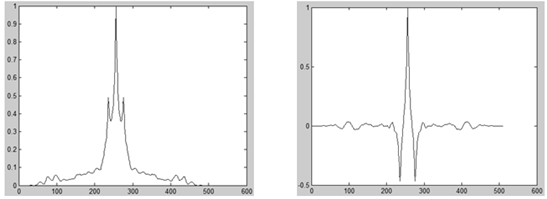
Рис.3 - Сечения АКФ соответственно  в плоскости, совпадающей с вектором движения

Первые два слагаемых в формулах (3) определяют основную форму и абсолютный максимум АКФ в центральной точке, вторые два слагаемых дают локальные максимумы для  и минимумы для , смещенные соответственно влево и вправо относительно центра АКФ на величину Δ. Очевидно, минимумы на АКФ() выделить проще на фоне абсолютного максимума, расстояние между ними равно  и его измерение может быть использовано в формуле (1) для определения скорости движения изображения. Тем не менее, в  силу симметрии АКФ, возникает проблема неоднозначности при определении направления вектора скорости (его начала и конца). Решить ее можно используя взаимно корреляционные функции. Форма ВКФ() имеет два ярко выраженных пика, соответствующих началу и концу вектора движения изображения. Один из пиков, соответствующий начальной точке вектора , расположен всегда в центре корреляционной плоскости. Второй пик соответствует конечной точке вектора  и перемещается по корреляционной плоскости при изменении модуля и направления вектора скорости, что позволяет однозначно измерить вектор движения изображения в диапазоне 0÷360гр.

Рис. 4 - Корреляционная плоскость . Яркие точки соответствуют корреляционным пикам

Очевидно, для расчета вектора скорости достаточно найти положение второго пика, т.к. первый пик всегда фиксирован в центре корреляционной плоскости, как показано на рис. 4. В этом случае отпадает необходимость суммирования разностных изображений, что упрощает задачу. Достаточно найти ВКФ определить положение максимума относительно центральной точки корреляционной плоскости.

Проведенное моделирование показало эффективность использования описанной методики для измерения вектора скорости движения изображения. Выбор порога Θ не столь критичен, как при яркостной бинаризации исходных изображений. В модели порог менялся в диапазоне от 0,05 до 0,8 максимальной яркости.

Для повышения быстродействия вместо вычисления ВКФ по классической формуле в модели опробована более простая метрика сравнения разностных изображений логического типа

что позволило сократить временные затраты на поиск максимума приблизительно в 6 раз. Диапазон измеряемых сдвигов Δ составляет 1÷40% от M при сохранении погрешности в пределах одного пикселя. При больших сдвигах существенное влияние оказывают краевые эффекты.

Литература

1. Ян Ричардсон. Видеокодирование. Н.264 и MPEG-4 — стандарты нового поколения. – М.: Техносфера, 2005. – 368 с.
2. Еськов Д.Н., Ларионов Ю.П. и др. Автоматическая стабилизация оптического изображения / Под общ. ред. Д.Н. Еськова, В.А. Новикова. – Л.: Машиностроение, 1988. – 240 с.
3. Шапиро Л., Стокман Дж. Компьютерное зрение / Пер. с англ. – М.: БИНОМ. Лаборатория знаний, 2006. – 752с.
4. Lucas B.D. An Iterative Image Registration Technique with an Application to Stereo Vision / B.D. Lucas, T. Kanade // Proceedings of the 7th international joint conference on Artifical intelligence. – 1981. – Vol. 2. – P. 674-679.
5. Гонсалес Р., Вудс Р., Эддинс С. цифровая обработка изображений в среде MATLAB. – М.: Техносфера, 2006. –616 с.
6. Фу К., Гонсалес Р., Ли К. Робототехника: Пер. с англ. – М.: Мир 1989. – 624 с.
7. Грузман И.С., Киричук В.С. и др. Цифровая обработка изображений в информационных системах: Учеб. Пособие. – Новосибирск: Изд-во НГТУ, 2002. – 352 с.
8. Красовский А.А., Белоглазов И.Н., Чигин Г.П. Теория корреляционно- экстремальных навигационных систем. – М.: Наука, 1979. – 408 с.
9. Козубовский С.Ф. Корреляционные экстремальные системы. – Киев: Наукова думка 1973. – 223 с.