ИЗУЧЕНИЕ ТЕРМИЧЕСКИХ НАПРЯЖЕНИЙ ПРИ НАГРЕВЕ ДИСПЕРСНО-УПРОЧНЕННОГО КОМПОЗИЦИОННОГО МАТЕРИАЛА

Пашинский В.В.¹, Субботина М.Г.²

¹Аспирант; ²доктор технических наук, доцент, Государственное высшее учебное заведение «Донецкий национальный технический университет»

ИЗУЧЕНИЕ ТЕРМИЧЕСКИХ НАПРЯЖЕНИЙ ПРИ НАГРЕВЕ ДИСПЕРСНО-УПРОЧНЕННОГО КОМПОЗИЦИОННОГО МАТЕРИАЛА

Аннотация

В статье исследовано изменение термических напряжений <σ> в композите Ni-TiC с содержанием TiC 7-52об.% при t=200…1000ºС. Установлено, что значения <σ> равны 8,3…10,5 Н/мм². При t<500°С напряжения возрастают, а при t=500…1000°С – снижаются.

Ключевые слова: композиционный материал, никель, карбид титана, термические напряжения.

Pashynsky V.V.¹, Subbotina M.G.²

¹Postgraduate student; ²D.Sci. (Eng.) Public higher education institution, Donetsk National Technical University

THE STUDY OF THE THERMAL STRESS IN DISPERSION-HARDENED COMPOSITE MATERIAL WHILE HEATING

Abstract

The average thermal stress <σ> in composite material Ni-TiC with 7-52vol.% of TiC at 200…1000ºC was studied in the article. It was proved that <σ> value was equal to 8,3…10.5 N/mm². The thermal stress was increasing while temperature was growing up to 500ºC, but when temperature gained 500ºC the stress began to decrease up to 1000ºC.

Keywords: composite materials, nickel, titanium carbide, thermal stress.

Одним из актуальных вопросов проектирования композиционных материалов является исследование локальных напряжений при внешних воздействиях различного вида. Большой интерес представляет установление результирующего влияния изменения объемов элементов неоднородностей (включений). Эти изменения могут быть вызваны различными факторами, например, температурой.

В данной работе были рассмотрены композиционные материалы, состоящие из металлической матрицы и тонкодисперсных тугоплавких частиц, не растворяющихся в основном металле (дисперсно-упрочненные материалы).

Целью работы было установление уровня термических напряжений в зависимости от доли включений карбида к материале при  нагреве.

Физико-математическое описание дисперсноупрочненного КМ

В работе были приняты следующие допущения: матрица и материал включений изотропны; упрочняющие частицы шарообразной формы; частицы расположены в матрице равномерно.

В большинстве случаев положение включений в объеме матрицы случайно, однако в целом материал является статистически однородным. Таким образом, выполняется гипотеза эргодичности, а значит, можно выделить некоторый усредненный объем, который можно назвать элементарным, где находится одно сферическое включение (рис. 1).

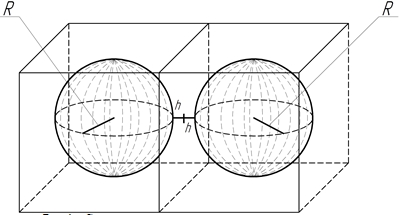
Рис. 1 – Схема расположения упрочняющих частиц в сплаве

Отдельное включение занимает объем куба с гранью l=2(h+R); объем элементарной ячейки V=l³=8(h+R)³. В дальнейшим индекс «в» обозначает величины, относящиеся к включениям, а «м» - к матрице.

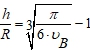Концентрация включений составляет . Таким образом, параметр h/R – характеристика микроструктуры КМ и равен . Очевидно, что при . Минимальное значение концентрации включений характеризует случай, когда h/R→∞, откуда ν_В→0. Данный диапазон концентрации включений соответствует границам применимости методов расчета свойств двухкомпонентных дисперсно-упрочненных КМ. В реальном композите объемное содержание упрочняющих частиц может быть значительно больше 52%, т.к. форма упрочняющих частиц далека от идеальной сферы, а сами частицы могут формировать непрерывный скелет.

Для расчета усредненных по объему термических напряжений можно воспользоваться уравнениями теории механики неоднородных сред для композита, в котором упругие модули матрицы меньше аналогичных модулей включений (случай «мягкая матрица – жесткие включения») [1-3]:

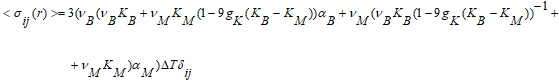где r – радиус-вектор случайной точки среды υ_В и υ_М – объемные доли включений и матрицы соответственно; K_М, K_В – объемные модули упругости матрицы и включений соответственно; α_В и α_М – коэффициент теплового расширения включений и матрицы соотвественно; δ_i,j - символ Кронекера (тензор второго ранга); ΔT – изменение температуры;

μ_М – сдвиговый модуль упругости матрицы.

Материал и методика

Моделирования был выбран композит, состоящий из никелевой матрицы и дисперсных частиц карбида титана при его объемном содержании от 7 до 52%.

Исходные данные:

1. размер частиц карбида титана R=0,005 мм
2. межчастичное расстояние H=0…0,1 мм
3. температура нагрева ΔТ=200…1000°С с шагом 100°С
4. модуль нормальной упругости никеля в зависимости от температуры приведен в таблице 1.
5. модуль сдвига никеля μ=73 ГПа
6. модуль нормальной упругости карбида титана К=460 ГПа
7. модуль сдвига карбида титана μ=410 ГПа
8. температурный коэффициент термического расширения никеля и карбида титана (табл. 1). При дальнейших расчетах используется функция интерполяции для определения температурного коэффициента при заданных температурах.

При дальнейших расчетах используется функция интерполяции для определения модулей упругости при заданных температурах.

Таблица 1 – Свойства Ni и TiC при различных температурах [4-6]

Ni	Т,°С К, ГПа	-269	20	120	200	300	380	480	520	590
		240	196	200	163,8	172,5	190,7	190,7	187	181,5
	Т,°С α, 106,°С-1	-0,15	299,85	369,85	389,85	399,85	599,85
		13,5	16,6	26	15	17,6	17,8
TiС	Т,°С α, 106,°С-1	-23,15	26,85	226,85	426,85
		7,35	7,72	7,63	7,79

Расчет средних термических напряжений в материале в зависимости от температуры нагрева и объемного содержания включений карбида был проведен согласно приведенному ранее физико-математическому описанию с использованием пакета программ MathCad v14.

Результаты и обсуждение

В результате моделирования были получены расчетные зависимости температурных напряжений в материале в зависимости от объемной доли включений карбида титана в матрице из никеля. Установленные зависимости приведены на рис. 2.

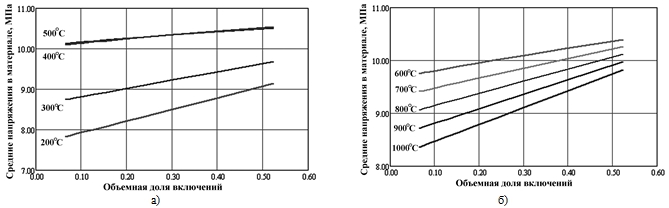
Рис.2 - Зависимость напряжений в композиционном материале от объемной доли включений карбида титана в матрице из никеля при температуре 200…500°С (а) и 600…1000°С (б)

На основании полученных результатов можно утверждать, что зависимость напряжений, вызванных нагревом, не является линейной относительно концентрации элементов неоднородности. Рост напряжений связан с увеличением доли частиц второй фазы прямопропорционально.

При увеличении температуры изменение напряжений носит более сложный характер. При увеличении температуры до 500°С напряжения в материале возрастают, а свыше 500°С до 1000°С – снижаются. Такие результаты могут быть обусловлены исходными значениями физических величин, которые являются справочными.

Установленные значения напряжений колеблются в пределах 8,3…10,5 Н/мм².

Заключение

В результате проведенного моделирования были получены данные о термических напряжениях в композиционном материале на основе никеля с включениями карбида титана (радиусом 5 мкм) при температуре 200…1000°С.

Были установлены следующие закономерности:

• Зависимость напряжений, вызванных нагревом, не является линейной относительно концентрации частиц карбида титана.
• Рост напряжений связан с увеличением доли частиц второй фазы прямопропорционально.
• При увеличении температуры до 500°С напряжения в материале возрастают, а свыше 500°С до 1000°С – снижаются.

Полученные значения напряжений лежат в диапазоне 8,3…10,5 Н/мм².

Используемый метод моделирования является достаточно чувствительным как к исходным значениям физических и механических величин, так и к методам прогнозирования этих значений для высоких температур нагрева. Следовательно, уменьшение погрешности, вносимой указанными факторами, является направлением для дальнейшего совершенствования данного метода установления уровня термических напряжений в композиционных материалах.

Литература

1. Колесников В.И., Бардушкин В.В., Сычев А.П., Яковлев В.Б. Напряженное состояние композиционных материалов в условиях воздействия термодинамических факторов // Вестник Южного научного центра РАН. – 2005. – № 4. – с. 9-13.
2. Кузнецов С.В. Эффективные тензоры упругости дисперсных композитов // Прикладная математика и механика. – 1993. – вып.1. – с.103-109.
3. Ошмян В.Г, Кнунянц Н.Н., Товмавсян Ю.М., Тополкараев В.А., Маневич Л.И. Теоретико-экспериментальное исследование статистического деформирования дисперсно-наполненных композитов // Механика композиционных материалов. – 1984. – № 3. – с.431-438.
4. Бернштейн М.Л., Займовский В.А. Механические свойства металлов. М. Металлургия, 1977, 496 с.
5. Чиркин В.С. Теплофизические свойства материалов ядерной техники. Справочник. М.: Атомиздат, 1968, 485 с.
6. Дриц М.Е. Свойства элементов. Справоник. М.: Металлургия, 1985, 672 с.