TriMetric Fusion: новый алгоритм для принятия многокритериальных решений

Multi-Criteria Decision-Making (MCDM) is a fundamental discipline in the field of decision-making that addresses the complexities of evaluating, ranking, and selecting optimal alternatives from a set of available options by considering multiple, often conflicting, criteria. The application of MCDM spans a wide array of fields, including engineering, economics, management, healthcare, and environmental science

Various MCDM methodologies have been developed, such as the Simple Additive Weighting (SAW)

To address these persistent challenges, we introduce the TriMetric Fusion (TMF) algorithm, a novel approach that integrates three distinct metrics into a unified decision-making framework. The TMF algorithm synthesizes:

Criteria Aggregated Weighted Index (CAWI): A weighted aggregation mechanism to quantify the cumulative performance of alternatives across all criteria.

Balanced Extreme Criteria Index (BECI): A metric designed to balance the influence of extreme performances.

Euclidean Distance: A measure to evaluate the deviation of alternatives from a predefined ideal solution, enhancing the precision of the ranking process.

These components operate within the TOPSIS algorithm, which provides a systematic mechanism for identifying the best alternative based on its relative closeness to the ideal solution of the set of aggregating metrics. Unlike conventional methods, TMF redefines the ideal solution using the measurement scales of the criteria rather than the values of the available alternatives, ensuring stability and consistency in rankings even when the set of alternatives changes. Moreover, TMF handles both maximization and minimization criteria within a unified framework, enhancing its adaptability and applicability across diverse decision contexts.

2.1. MCDM problem formulating

TMF algorithm is a sophisticated decision-making tool designed to evaluate alternatives based on multiple criteria, integrating three distinct metrics: CAWI, BECI, and the Euclidean distance. These metrics are synthesized using the TOPSIS to compute a final ranking. The combination of these metrics ensures a comprehensive analysis that captures different dimensions of the data.

A MCDM problem can be mathematically defined as the process of finding the best alternative from a set of available options based on multiple criteria. Formally, this can be represented as follows:

Let be the set of alternatives (options) and be the set of criteria. Each alternative is evaluated according to each criterion , resulting in a decision matrix of size , where each element represents the performance of the alternative  with respect to the criterion . The goal of MCDM is to select the best or order alternative(s) based on these evaluations.

2.2. Data Processing

The following conditions must be met, to ensure the successful operation of the TMF algorithm:

1. Positivity: All input values must be strictly positive. Due to computing ratios using the values associated with each alternative and the ideal solution, as in Equations

2. Completeness: The dataset must not contain any missing values. Missing data can lead to biased or incorrect calculations and ultimately affect the decision-making process. Ensuring completeness either through data preprocessing steps like imputation or by requiring fully populated datasets is crucial.

2.3. Defining the Ideal Solution in MCDM and TMF

The ideal solution in an MCDM problem is a hypothetical alternative that optimally satisfies all the decision criteria, serving as a benchmark for evaluating all other alternatives. Mathematically, the ideal solution can be defined as:

(1)

where:

for maximization criteria 

for minimization criteria

This definition ensures that the ideal solution reflects the best possible scenario for each criterion. However, a novel method proposed for defining involves setting its components at the extremes of the measurement scale used for each criterion to avoid the reversal problem often encountered in MCDM. Specifically:

- For maximization criteria , set equal to the maximum measurable or expected value of .

- For minimization criteria , set  equal to the minimum measurable or expected value of .

This method uses the minimum and maximum of the scales that measure each criterion to define the ideal solution, ensuring that the ideal values remain consistent and unaffected by the dynamic changes in the set of alternatives. This approach prevents the rankings of the existing alternatives from being illogically altered when new alternatives are added or existing ones are removed, thereby enhancing the stability and reliability of the decision-making process.

2.4. Ratio to the Ideal Solution

To ensure that each criterion is appropriately scaled and comparable, normalization against the ideal solution is conducted as follows:

- For maximization criteria:

(2)

- For minimization criteria:

(3)

Where:

-  denotes the actual measured value of the -th criterion for the -th alternative.

- represents the ideal value for the -th criterion.

This normalization approach ensures that each criterion is evaluated on a scale relative to an ideal benchmark, facilitating a balanced and effective aggregation of diverse criteria into a single composite score through CAWI, BECI, and distance. This method enhances the consistency and reliability of evaluations, especially in dynamic scenarios where the set of alternatives might change. The normalization by the ideal solution for each criterion ensures that the alternatives are comparable across criteria with different scales or units.

2.5. TriMetric Fusion metrics

2.5.1. Criteria Aggregated Weighted Index (CAWI)

CAWI is a linear scoring function designed to aggregate the ratio of the performance of each criterion to the value of the ideal solution for that criterion, weighted according to its importance. The formulation of CAWI is given by the Equation

(4)

Where:

- is the ratio of the actual value of the -th criterion for the -th alternative to the value of the ideal solution for that criterion.

- represents the weight assigned to the -th criterion, indicating its relative importance in the decision-making process.

-  is the total number of criteria.

2.5.2. Balanced Extreme Criteria Index (BECI)

BECI addresses the potential bias in CAWI that might overlook the performance at the extremes (both best and worst). It computes a score based on a balanced view of the most favorable and least favorable performances. The BECI is calculated as in the Equation

(5)

where:

- is a parameter that balances the influence of the maximum and minimum scores, typically set to 0.5 to equally weight both extremes.

There are two approaches to order the alternatives (max-scoring decision-making: max of maximum values of alternatives and min-scoring decision-making: max of minimum values of alternatives).

 plays a major role in determining the amount of bias in alternatives, which reflects the way of making the decision. For example, in terms of max-scoring decision-making, when we set , the final ranking only focuses on max of criteria without taking into consideration minimum of criteria (high bias). To reduce bias, we can vary  to balance between max and min, and choosing this parameter depends on the priority and nature of the problem.

2.5.3. Distance from Ideal Solution (DIS)

The DIS metric enhances the TriMetric Fusion algorithm by quantifying how far each alternative deviates from the optimal performance across all criteria. This measure is crucial for identifying alternatives that not only perform well on CAWI or BECI, but also consistently align closely with the ideal performance benchmarks.

The formulation of DIS is given by the Euclidean formula, as in Equation

(6)

The DIS metric fundamentally captures the Euclidean distance, a direct and intuitive measure of spatial discrepancy between each alternative’s performance vector and the vector of ideal solution, which equals ones in the case of getting the maximum and minimum measurable or expected values of .

2.5.4. Similarity Index Calculation and Ranking (TOPSIS-based)

TOPSIS is employed to rank the set of three metrics based on their similarity to the ideal solution, which is defined uniquely by the maximum scores of CAWI and BECI and the minimum of the DIS. This approach helps to determine the most optimal alternatives by comparing how close each one based on its metrics is to the ideal solution. It computes the similarity index as in Equation

(7)

where:

- is the distance of the -th alternative from the ideal solution.

- is the distance from the worst (negative ideal) solution.

3.1. Experimental Environment

The path-finding experiment was conducted in a two-dimensional discrete grid environment representing a robotic navigation scenario, as in

1. Boundary Walls: Rectangular borders were established at x and y coordinates of -10 and 60 meters.

2. Internal Obstacles: Two vertical obstacle walls were placed at x-coordinates 20 and 40 meters, intersecting with the horizontal plane.

The robot was modeled with Radius of 1 meter, eight directional movements (cardinal and diagonal), and variable energy and path traversal costs for different directional movements.

3.2. Motion Model

The movement costs that reflect the motion model in the simulation were shown in Table 1. We notice that the straight movements have a path cost of 1 and diagonal movements have a reduced path cost of 0.5, but with have higher energy costs. Energy costs increase progressively for different movement directions.

3.3. TriMetric Fusion Algorithm Configuration

The algorithm evaluates path candidates based on three primary criteria:

1. Path Cost

2. Distance to Goal

3. Energy Consumption

- Criteria Types: Minimization for all three metrics

- Weighting Scheme:

We investigated three distinct weight configurations to evaluate the TriMetric Fusion (TMF) algorithm's path-finding capabilities:

Configuration 1: Balanced Approach

- Weight Vector: 

- Interpretation: Equal importance to path cost, energy consumption, and distance

Configuration 2: Energy-Prioritized

- Weight Vector:

- Interpretation: Emphasizing energy efficiency while maintaining path cost and distance considerations

Configuration 3: Cost-Minimization

- Weight Vector:

- Interpretation: Prioritizing minimal path cost with moderate energy and distance constraints

- Ideal Solution Reference: Minimal values 

3.4. Performance Metrics

The performance metrics for each configuration are summarized in Table 2.

3.5. Validating with Dijkstra’s algorithm (Comparative Analysis)

Path Length and Nodes Traversed:

All configurations of the TMF algorithm, as well as Dijkstra's algorithm, resulted in the same path length of 76.37 meters except Energy-Prioritized with 77.97 meters, traversing 52 nodes. This indicates that all methods converged approximately to the same optimal path in terms of distance, demonstrating the effectiveness of TMF in maintaining path efficiency while incorporating additional criteria.

Energy Consumption:

The Energy-Prioritized configuration of TMF achieved the lowest energy consumption at 79.79, matching Dijkstra's performance. This configuration demonstrated a 6.6%, 3.4% reduction in energy consumption compared to the Cost-Minimization and Balanced Approach respectively, highlighting its efficacy in energy-efficient scenarios. The Cost-Minimization configuration, while prioritizing path cost, resulted in the highest energy consumption at 85.4, indicating a trade-off between cost and energy efficiency.

Path Cost:

The Cost-Minimization configuration achieved the lowest path cost at 33.0, a 10.8% reduction compared to the Energy-Prioritized and Dijkstra's algorithm. This configuration's ability to minimize traversal expenses underscores its utility in scenarios where cost is a critical factor.

Computation Time:

The computation times for the TMF configurations were slightly higher than Dijkstra's algorithm, with the Balanced Approach and Cost-Minimization configurations both at 0.73 seconds, and the Energy-Prioritized configuration at 0.76 seconds, compared to Dijkstra's 0.6 seconds. This marginal increase in computation time is a reasonable trade-off for the added benefits of multi-criteria optimization.

Nodes Visited and Search Space:

In the context of pathfinding algorithms, Visited Nodes refers to a set contains all the nodes that have already been visited and evaluated by the algorithm. Once a node is added to it, it means that the algorithm has already considered all possible paths through this node, and it will not be revisited. Nodes' Search Space refers to a set contains all the nodes that are candidates for exploration. These nodes are part of the search space that the algorithm will consider next. The algorithm will pick the most promising node from it to evaluate in the next step.

The Balanced Approach visited 621 nodes, fewer than Dijkstra's 707, indicating more efficient exploration. However, the Energy-Prioritized configuration visited 700 nodes, slightly fewer than Dijkstra's, while the Cost-Minimization configuration visited 654 nodes. The search space explored by the Balanced Approach and Cost-Minimization configurations was 1168 and 1158 nodes, respectively, both less than Dijkstra's 1230 nodes. The Energy-Prioritized configuration explored the smallest search space at 828 nodes, demonstrating its efficiency in energy-focused scenarios.

The results indicate that the TMF algorithm effectively balances multiple criteria in path-finding, offering a flexible approach to robotic navigation. The balanced approach provided a moderate path with uniform characteristics, suitable for scenarios requiring equilibrium between path cost, energy, and distance. The energy-prioritized configuration demonstrated a 3.4% reduction in energy consumption, albeit with a slightly longer path, highlighting its efficacy in energy-efficient scenarios. Conversely, the cost-minimization configuration achieved the lowest path cost, albeit with a slight increase in energy consumption.

Compared to Dijkstra's algorithm, TMF showed adaptability in handling multi-criteria decision-making, which is crucial in real-world robotic applications where multiple performance metrics often present. The computational efficiency of TMF was comparable to Dijkstra's, with slight variations depending on the weight configuration.

3.6. Visualization Insights

Figure 1 illustrates the path trajectories for the different weight configurations and Dijkstra’s algorithm. The nodes are color-coded to represent search space and final path, showing variations in path length and curvature while maintaining consistent obstacle avoidance strategies.

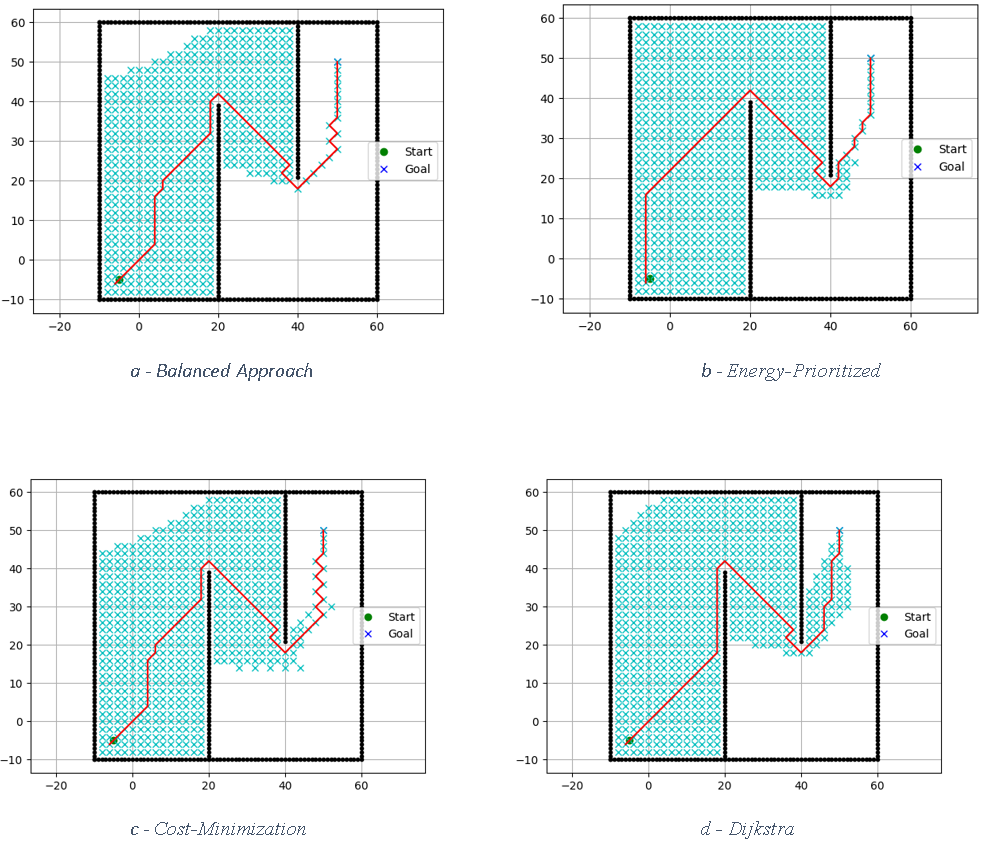
Figure 1 - Comparative Path Trajectories for Different Weight Configurations and Dijkstra's algorithm

DOI:10.60797/IRJ.2025.153.6.3

This study introduced the TriMetric Fusion (TMF) algorithm, a novel multi-criteria decision-making (MCDM) approach designed to address complex decision problems by integrating three key metrics: the Criteria Aggregated Weighted Index (CAWI), the Balanced Extreme Criteria Index (BECI), and the Euclidean distance. The TMF algorithm synthesizes these metrics within the TOPSIS framework, enabling a comprehensive evaluation of alternatives based on multiple criteria. To validate its effectiveness, the algorithm was applied to a robotic pathfinding problem, demonstrating its ability to balance competing objectives such as path cost, energy consumption, and distance. The experimental results confirmed that TMF offers a flexible and robust solution for decision-making in complex scenarios, outperforming in some cases traditional methods like Dijkstra's algorithm in multi-criteria optimization tasks. This application served as a practical demonstration of TMF's capabilities, highlighting its potential for broader use in MCDM problems beyond pathfinding.

TMF's flexibility in weighting and criteria handling allows it to manage both maximization and minimization criteria within a unified framework, making it adaptable to a wide range of decision-making scenarios, as demonstrated in the pathfinding application where it successfully balanced path cost, energy consumption, and distance. Additionally, TMF ensures stability and consistency by defining the ideal solution based on measurement scales rather than the dataset itself, effectively avoiding the "rank reversal" problem common in MCDM methods and ensuring reliable rankings even with dynamic changes in alternatives. Despite its multi-criteria nature, TMF maintains computational efficiency, processing complex decision problems with minimal overhead, as evidenced in the pathfinding demonstration, making it suitable for real-world applications. Finally, the demonstration of applicability in robotic pathfinding validated TMF's effectiveness, showcasing its ability to optimize multiple conflicting objectives and providing a proof of concept for its broader applicability in diverse MCDM problems.

While the TriMetric Fusion (TMF) algorithm has demonstrated significant potential, several limitations should be acknowledged. The current implementation assumes static criteria and weights, which may not fully capture the dynamic nature of some real-world decision problems. Additionally, the algorithm's scalability in high-dimensional problems has not been thoroughly tested, and its computational complexity may increase with a large number of criteria or alternatives. TMF also relies on normalization techniques to handle criteria of different scales, which may introduce biases if not carefully implemented. Furthermore, while Euclidean distance was used in this study, the impact of other distance metrics (e.g., Manhattan, Mahalanobis) on TMF's performance remains unexplored. To address these limitations and further enhance the TMF algorithm, several research directions are proposed. These include developing mechanisms for dynamic weight adjustment to adapt to changing conditions, investigating TMF's scalability in high-dimensional optimization problems, and integrating machine learning techniques to optimize parameters such as weights and distance metrics. Additionally, extending TMF's application to diverse domains like supply chain management, healthcare decision-making, or financial portfolio optimization would validate its generalizability. Conducting comparative studies with other state-of-the-art MCDM methods would further establish TMF's advantages and limitations, while exploring enhanced normalization techniques could improve its handling of criteria with varying scales and units. These future investigations aim to refine TMF and expand its applicability to a broader range of complex decision-making scenarios.