Модель идентификации состояния подвижного состава при его движении на основе оптического сенсора

Одним из наиболее значимых является вопрос определения состояния состава, движущегося на инфраструктуре, и его местоположения. Сигнал, поступающий с оптического сенсора, содержит достаточно много информации. Обработка этой информации с использованием нетрадиционных подходов позволит по-новому решить актуальные вопросы оценки состояния движущихся по инфраструктуре объектов.

Известно, что целостность состава определяется с использованием точечных датчиков, устанавливаемых на пути. При известном количестве вагонов рассчитывается число срабатываний датчика, тем самым подтверждается, что разрыва состава не произошло. В работах

Необходимо отметить, что частота опроса сенсора позволяет с достаточной точностью определять местоположение состава, конкурируя с инерциальными системами, с системами спутниковой навигации, подверженными, как известно, влиянию систем радиоэлектронной борьбы.

Переход к использованию высокоскоростного транспорта (в особенности магнитолевитационного) требует совершенного построения системы управления движением, где не будет использоваться в качестве основного датчика определения местоположения поезда рельсовая цепь.

Достоверность определения проезда состава с использованием оптического сенсора зависит от помех, в частности, когда присутствует максимальный уровень помех при проезде двух встречно идущих составов. Модель, реализованная на использовании одного распределенного сенсора (рефлектометра), не точно оценивает данную ситуацию, а это ведет к тому, что достоверность существенно снижается и использовать данное техническое решение не представляется возможным. В этой связи предложен другой подход, основанный на использовании технологии мультиплексирования с разделением по длинам волн (WDM).

Цель работы – оценить достоверность контроля проезда колесных пар с использованием технического решения без технологии WDM и разработать теоретические основы для модели контроля состояния подвижного состава с использованием технологии WDM.

Рассмотрим сигнал, поступающий с сенсорного датчика от движущегося состава. Сигнал дискретен по времени частота 0.0004 (2500 Гц). Матрица n × n по горизонтали продолжительность считывания n × Δt количество отсчетов с Δt = 0,000001 c, по вертикали продолжительность снятия отсчетов дискретностью 0,004 с.

Измеряемые значения нормализуем с использованием min – max нормализацией:

(1)

где:

min(ut) – минимальное значение ut  в рассматриваемом интервале;

max(ut) – максимальное значение ut  в том же интервале.

Все значения u с рефлектометра будут находиться в интервале от 0 до 1.

Для оценки проезда колесных пар проведем нелинейную фильтрацию сигнала – экспандирование. Фильтрация необходима для масштабирования сигнала в области больших значений амплитуд сигналов с целью более четкого представления картины воздействия колебаний на сенсор. Это осуществляется с использованием формулы u = u2.

Рассмотрим сигнал от подвижного состава, получаемый при проезде колесных пар. Определяем среднее значение сигнала на интервалах sj

(2)

где  определяется количеством отсчетов в матрице на принятом интервале.

При скорости 360 км/ч ошибка определения локации колеса при соседних отсчетах 4 см. Это расстояние, проходимое колесом между двумя измерениями с частотой 2500 Гц. Рефлектометр измеряет сигнал  с сенсора частотой до 100 мГц. Это соответствует точности измерения 4 мм при длине участка 40 км. Выбираем n = 10. Рассчитываем средние значения по всей длине состава. Матрица  свертки 100 × 1. Превышения среднего значения в 1,2 раза свидетельствует о проезде колеса в точке локации пути.

При проезде колесной пары координаты  на инфраструктуре в ближайшей области сенсора возникают большие по амплитуде колебания.  Через расстояние lk между колесными парами присутствует максимальный сигнал от второй колесной пары. Находим максимальные величины амплитуды в этих областях, показанных на рисунке 1 – это Umax1, Umax2. Строим через эти точки прямую u1, решая систему:

(3)

где:

 – коэффициенты уравнения;

 – точки локации на инфраструктуре.

Получаем уравнение прямой u1:

(4)

Находим точку с минимальным значением амплитуды Umin. Далее строим две прямые проходящие через точки Umax1, Umin и Umax2, Umin аналогично формуле (1), получаем уравнения прямых u2, u2:

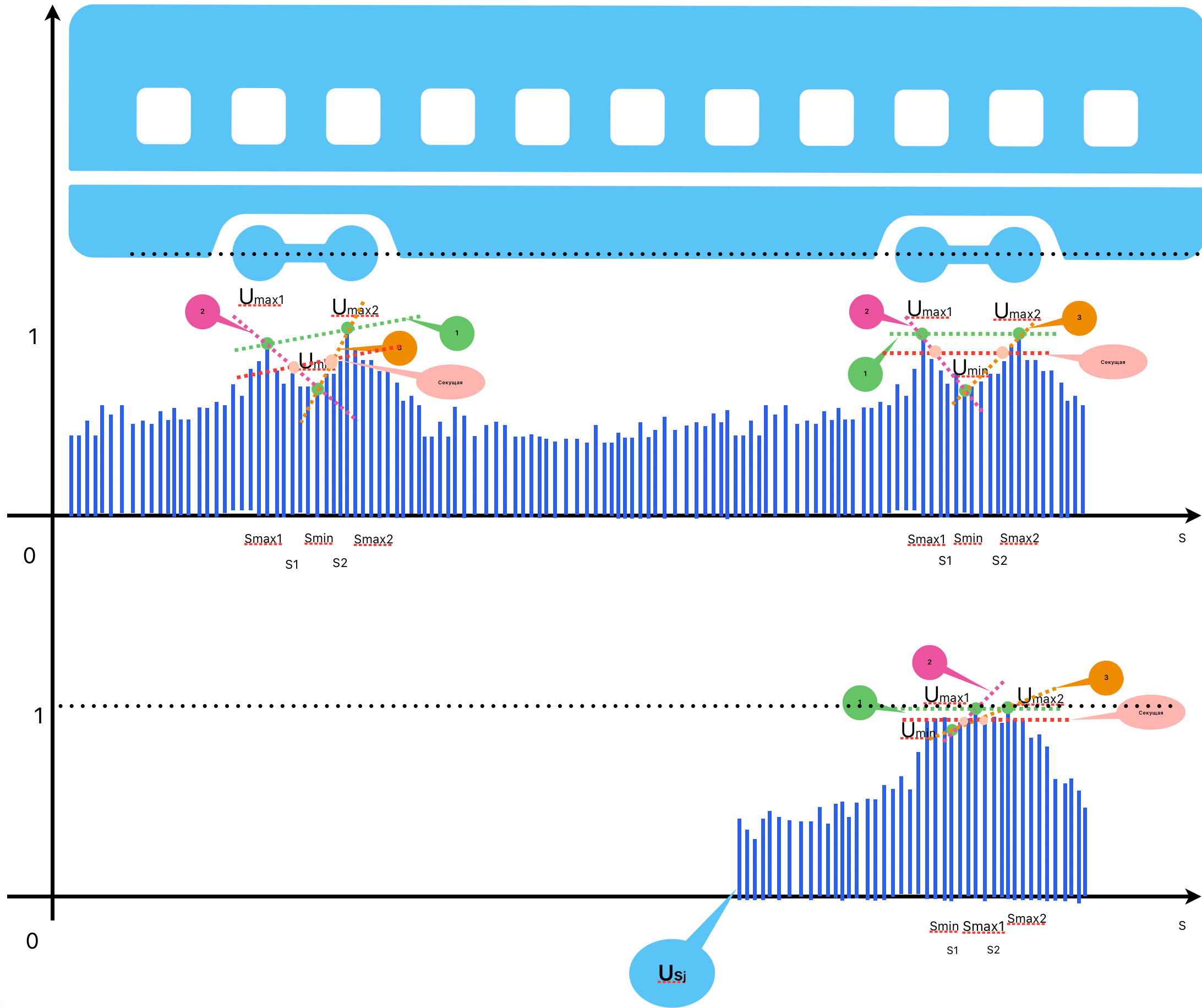
Рисунок 1 - К модели определение проезда колесных пар

DOI:10.60797/IRJ.2025.153.117.1

(5)

По сути, это преобразование представляет линеаризацию участка характеристики между проезжающими колесами и формирование изображения с помощью двух прямых, характеризующих возникающую зависимость между сигналами при проезде колесных пар.      

Строим секущую параллельную прямой us || u1:

(6)

где  – смещение секущей us, выбираем 

Определяем две точки пересечения секущей us с прямыми u2, u3 решая системы:

- точка пересечения секуще us и прямой u2

(7)

получаем точку s3;

- точка пересечения секуще us и прямой u3

(8)

получаем точку s4.

Полученные точки показывают, что определены колесные пары, проследовавшие точки локации s1, s2 и s3, s4.

Далее, зная число вагонов в составе nc, определяем число колесных пар, которые находятся на заданном расстоянии друг от друга (рисунок 2). На рисунке 2 l1, l2, l3 зависят от типа подвижного состава, в случае разрыва состава изменится параметр l2 — расстояние между колесным парами в соседних вагонах. Таким образом, обеспечивается контроль  целостности состава.

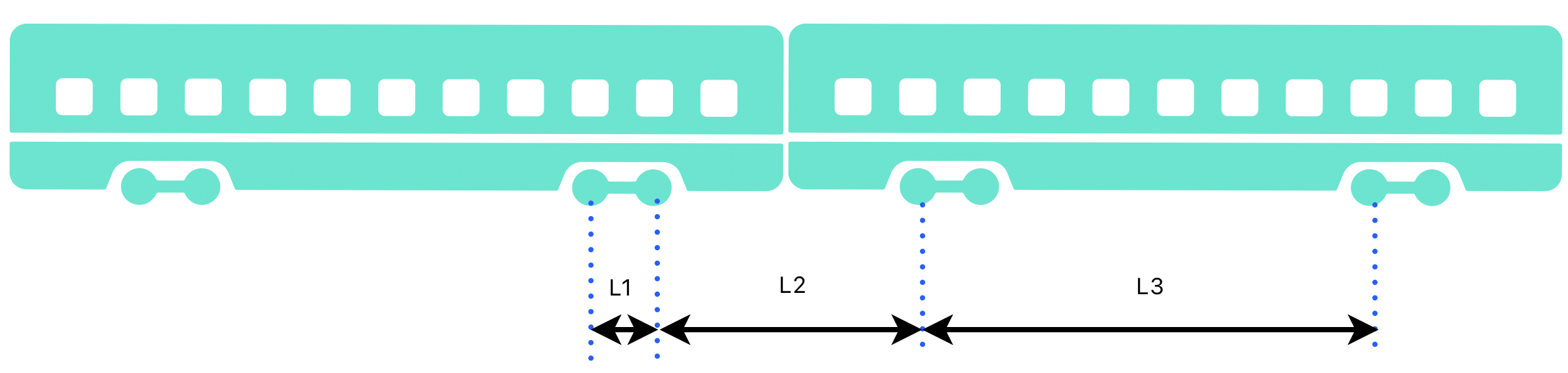
Рисунок 2 - Размеры расстояний колесных пар в вагоне

Примечание: l1 — расстояние между колесами тележки; l2 — расстояние между колесными парами соседних вагонов по всему составу; l3 — расстояние между тележками вагона

DOI:10.60797/IRJ.2025.153.117.2

Поставим задачу определения достоверности модели определения целостности состава. Обратимся к рисунку 3. Модель будет работоспособна, если помехи, действующие на максимальные и минимальные значения амплитуды при проезде колесных пар, не приводят к тому, что сигнал от максимальной амплитуды становится ниже, чем сигнал, соответствующий секущей Us, а минимальный сигнал становится выше по уровню, нежели сигнал от секущей Us:

(9)

где Us – сигнал помехи.

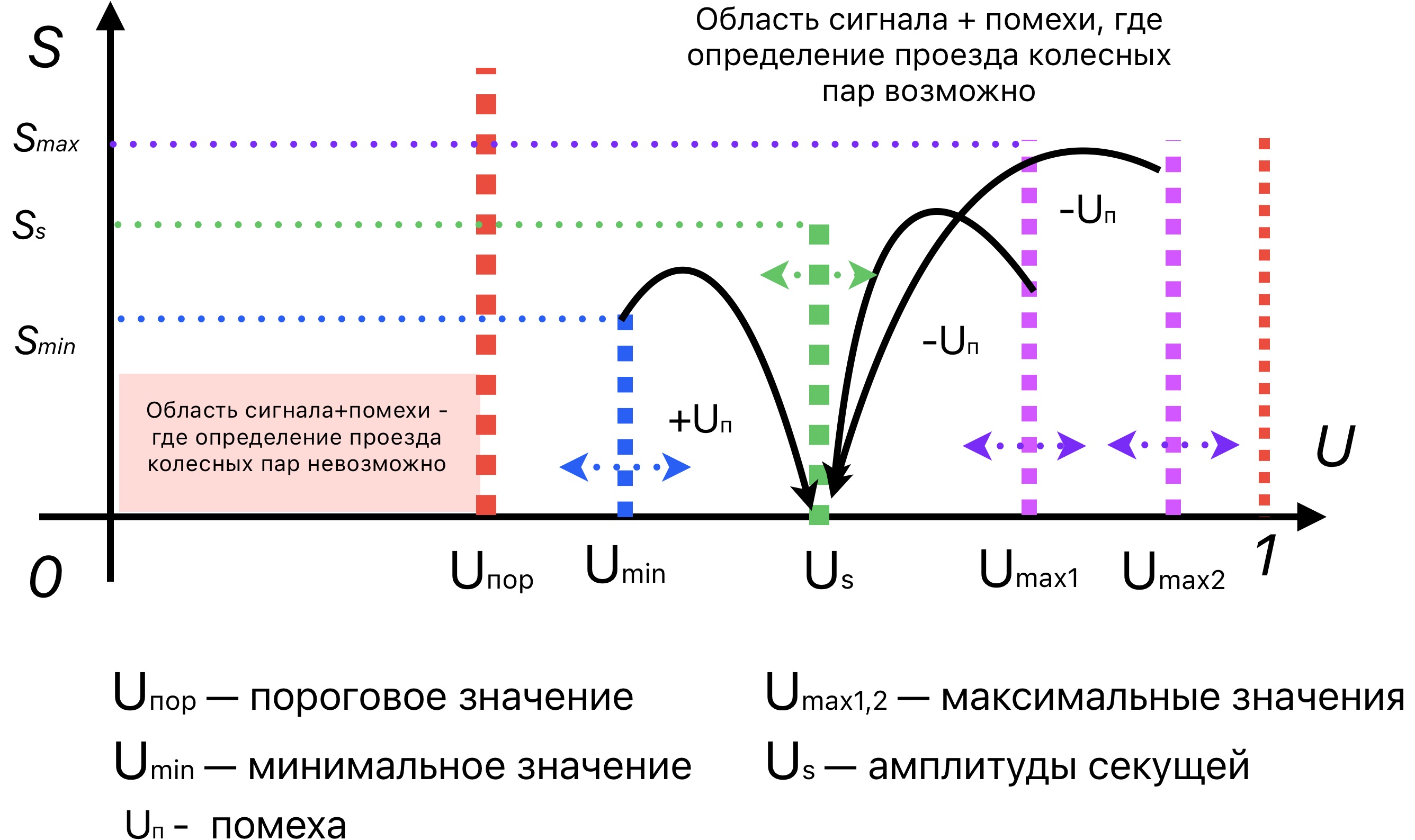
Рисунок 3 - Воздействие помех для определения проезда колесных пар

DOI:10.60797/IRJ.2025.153.117.3

На рисунке 3 отображена область, где из-за действия помех определение проезда колесных пар невозможно. Величина порогового значения Unop, ниже которого невозможно определить проезд колесных пар, вычисляется:

(10)

где Uj  – значения амплитуд сигнала и помехи, измеренные  по всей длине состава.

Значение достоверности Pd модели определяется в соответствии с

(11)

где P1,2  – вероятности ошибок первого и второго рода или вероятности ложного и необнаруженного отказа модели.

Величина вероятности ошибки первого и второго рода определятся в соответствии с рисунком 3 и вычисляется:

(12)

где  – плотности распределения сигналов максимальной и минимальной амплитуд и помехи.

Величина 1 в верхнем пределе интегралов соответствует нормированной величине амплитуды. Обработка сигналов и помехи по критерию X2 – Пирсона

Плотность нормального распределения umax и umin сигналов

(13)

где  – дисперсия сигнала.

Плотность распределения помехи представляет сигнал нулевым средним Um = 0

(14)

где  – дисперсия сигнала.

Решение (2) осуществляем через замену экспоненты рядом Маклорена (Тейлора)

(15)

Подставим (5), (4), (3) в (2) получим

(16)

где a, b, c, d, e, f – новые пределы интегрирования:

(17)

Заменяя  интегрируем и применяя формулу Коши

(18)

где  – количество членов определяющих точность вычисления интегралов.

Результаты расчета достоверности приведены в таблице 1.

Дальнейшее развитие метода связано с применением технологии WDM в сенсорном датчике, проложенном вдоль железнодорожной инфраструктуры

При использовании технологии мультиплексирования с разделением по длинам волн (Wavelength Division Multiplexing, WDM) в оптических кабелях происходит интерференция световых потоков, обусловленная механическим воздействием на кабель. Это происходит в связи с тем, что механические деформации, такие как изгибы, сжатие или вибрации, изменяют свойства оптического волокна, влияя на распространение световых сигналов.

Физическое объяснением возникновения механизма интерференции. Интерференция световых потоков в WDM-системах возникает из-за изменений фазовых характеристик световых волн при их прохождении через деформированное оптическое волокно. В оптических системах, где используются несколько длин волн, механическое воздействие приводит к следующим эффектам:

- изменение длины пути света: когда оптическое волокно деформируется, длина пути, по которому проходит свет, может изменяться. Это влияет на фазу световых волн, что может привести к изменению условий интерференции между различными длинами волн;

- поляризационные эффекты: механические деформации могут также изменять поляризацию световых волн. В результате разные моды или длины волн могут интерферировать друг с другом, что приводит к искажениям в световых потоках;

- модовые интерференции: в многомодовом волокне механическое воздействие может вызвать смешивание мод, что также ведет к интерференции и появлению новых частот сигналов (четырехволновое смешение FWM: если в волокне передаются три сигнала с частотами , FWM может создавать новые частоты , которые удовлетворяют условию: ).

Реакция на механические колебания, создаваемые различными источниками, зависит от ряда факторов, таких как тип и частота колебаний, длины волн, используемые в системе, а также характеристики самого оптического волокна.

Основные аспекты реакции оптического сенсора:

- на колебания, создаваемые поездом, обычно имеют более низкую частоту и большую амплитуду. Такие колебания могут вызывать значительные механические деформации оптического волокна, что приводит к заметным изменениям в фазе и интенсивности сигналов;

- на колебания, создаваемые человеком, обычно имеют более высокую частоту и меньшую амплитуду;

Зависимость реакции оптического сенсора от длины волны (WDM):

- в системе WDM различные длины волн могут по-разному реагировать на одни и те же механические колебания из-за различий в фазовой чувствительности. Это связано с тем, что различные длины волн могут испытывать разные фазовые сдвиги и изменения интенсивности при прохождении через одно и то же деформированное волокно. Более короткие длины волн могут быть более чувствительны к небольшим деформациям, тогда как более длинные волны могут лучше отражать крупные деформации;

Интерференционные эффекты:

- в результате механических колебаний возникает фазовый сдвиг сигналов на различных длинах волн, что приводит к интерференции между этими сигналами. Например, для поезда, создающего сильные низкочастотные колебания, интерференция может быть более выраженной для длин волн, которые лучше чувствительны к низкочастотным деформациям. Для человека, создающего высокочастотные, но менее интенсивные колебания, интерференция будет более заметна на тех длинах волн, которые более чувствительны к высоким частотам;

- эффекты дисперсии и нелинейности: в одномодовом волокне нелинейные эффекты, такие как четырёхволновое смешение (FWM), могут усиливаться при наличии механических воздействий, особенно если используются высокие мощности сигналов. Эти эффекты могут влиять на качество демультиплексирования и приводить к дополнительной интерференции.

Модель реакции сенсора. Допустим, что система DAS использует оптический кабель с WDM и способна измерять изменения фазовых характеристик на нескольких длинах волн одновременно. При воздействии поезда колебания могут привести к следующей реакции:

- на определённой длине волны (например, ) может возникнуть фазовый сдвиг , который пропорционален величине деформации .

- на другой длине волны (например, ) фазовый сдвиг  может быть меньше или больше в зависимости от чувствительности этой длины волны к деформации.

Фазовые сдвиги для различных длин волн можно описать следующим образом

(19)

где:

 – длина волны;

 – изменение длины волокна для данной длины волны, вызванное механическим воздействием.

Для системы DAS с WDM важно учитывать реакцию разных длин волн на различные типы колебаний. Например:

1) для обнаружения и классификации поездов можно использовать длины волн, которые более чувствительны к низкочастотным и мощным колебаниям;

2) для определения целостности составов, при встречном движении.

3) для обнаружения присутствия человека можно использовать длины волн, чувствительные к высокочастотным и менее интенсивным колебаниям.

Такой подход позволяет отслеживать движение поездов, людей и других объектов в реальном времени, используя преимущества мультиплексирования с разделением по длинам волн.

Предлагаем математическое описание процесса определения параметров движения поезда с использованием фазовых данных осуществить следующим образом. Процесс включает анализ изменений фазового сдвига вдоль оптического кабеля и интерпретацию этих изменений для определения скорости и направления движения поезда.

Оценка фазового сдвига. Фазовые сдвиги в оптическом кабеле могут быть выражены как функция расстояния d и времени t. Пусть  – это фазовый сдвиг, который регистрируется в точке на расстоянии d от начальной точки и в момент времени t. Свяжем движение поезда с изменением  фазы. Когда поезд проходит мимо определённого участка, фаза света изменяется. Можно записать изменение фазы как разницу фаз между двумя точками d1 и d2: 

Определим скорость. Чтобы определить скорость поезда, можно использовать временные изменения фазового сдвига. Если поезд проходит между точками d1 и d2, изменение фазы во времени можно использовать для вычисления скорости . Вычислим время Δt, за которое поезд проходит между двумя точками. Это можно сделать на основе временных меток изменений фаз: . Если расстояние между точками d1 и d2 известно, скорость поезда  вычисляем как: .

Свяжем параметры изменения фазы во времени и по длине через дифференциальные уравнения для фазовых изменений:

(20)

 где  – это изменение фазы во времени, а  – это изменение фазы по длине кабеля. Эта модель позволяет связать фазовые изменения с движением поезда.

Применим ряд  Калмогорова-Габора к фазовому сдвигу

Ее разложение может быть представлено как:

(21)

где:

Amn – коэффициенты, учитывающие ковариацию времени и расстояния:

Pm(t) и Qn(d) – ортогональные функции времени и расстояния соответственно.

Для конкретного применения можно рационально выбрать подходящие ортогональные функции Pm(t) и Qn(d), например, полиномы или другие базисные функции, которые лучше всего соответствуют физическим условиям задачи. Суть применения многомерного ряда Калмогорова-Габора для анализа фазового сдвига от времени и расстояния состоит в том, что он позволяет провести анализ динамических процессов в оптическом кабеле. Для формализации задачи рассмотрим фазовый сигнал как функцию времени t и расстояния d, разложенную через ряд Калмогорова-Габора:

(22)

где:

Amn – коэффициенты, характеризующие ковариацию временных и пространственных переменных;

P(t) и Q(d) – базисные функции времени и расстояния.

Представим базисные функции через степенной ряд , а Перемножив ряды по формуле Коши

(23)

Далее подставим это разложение в исходное дифференциальное уравнение, связывающее фазу со временем и расстоянием, получим:

(24)

Решая это уравнение для каждого члена ряда, можно оценить изменения фазы как функцию времени и расстояния, что позволяет определить такие параметры, как скорость и направление движения поезда, анализируя фазовые сдвиги на каждой  из длин волн задействованных в WDM.

Альтернативным подходом является использование искусственной нейронной сети. Суть подхода состоит в том, что изменения механических параметров оптического сенсора приводит к интерференции волн. В результате получаем множество интерференционных изображений, зависящих от местоположения объектов на инфраструктуре. Каждый объект создает свой спектр механического воздействия на сенсор. В работе разработана модель распространения световых волн и возникновения интерференционных изображений при движении различных объектов по инфраструктуре. Как правило, для моделирования распространения оптических волн используют уравнение Шрёдингера

(25)

где:

 – комплексная амплитуда волны;

 – потенциальная энергия;

 и  – постоянная Планка и масса.

Это уравнение (11) позволяет анализировать как линейные, так и нелинейные волновые эффекты в оптических материалах. Амплитуду светового поля в уравнении Шрёдингера задаем как комплексную функцию, которая зависит от пространства и времени:

(26)

где:

A (z, t) – амплитуда, зависящая от координаты z и времени t;

 – фаза, также зависящая от z и t.

На основе (25, 26, 27 ) разработана эмитационная модель описывающая пути прохождения световых потоков в одномодовом кабеле. Рассмотрены следующие случаи:

- встречное движение составов;

- движение одиночного состава с расцепкой вагонов.

В модели приняты ограничения:

- состав рассматривается точечным, воздействие на сенсор в определеной точке пути;

- механические воздействия задаются частотами грузовыми , пассажирскими  и пригородными  составами;

- максимальная деформация сенсора составляет 0,5 мк;

- диаметр сердцевины оптического кабеля 5 мк.

В зависимости от условий задачи амплитуда (12) может быть задана как постоянная величина, или как функция, зависящая от затухания  или других параметров.

Решение уравнения Шрёдингера для оптики можно проводить несколькими методами, среди которых выбираем аналитический метод разложения в ряд (ряд Фурье):

(27)

где  – базисные функции ряда Фурье.

Результаты моделирования представлены ниже в таблице 2. Рассмотрен случай встречного движения подвижных составов, а также нахождения одиночного состава.

Математическое описание процесса определения движения поезда с использованием фазовых данных включает моделирование фазовых сдвигов, вычисление скорости и направление на основе анализа временных изменений фаз. Эти методы позволяют определять характеристики движения поезда, используя данные, собранные с оптического кабеля.

Использование многомерного ряда Калмогорова-Габора для описания фазового сдвига в оптическом кабеле позволил связать фазовые изменения со временем и локализацией места проезда составом.

Оптические сенсоры на базе DAS с использованием технологии WDM могут различным образом реагировать на механические колебания, создаваемые различными источниками, такими как поезд или человек. Эта реакция зависит от частоты и амплитуды колебаний, а также от длины волны, используемой в системе. Многоволновые системы позволяют более качественнее анализировать и классифицировать различные стадии состояния объектов на инфраструктуре, за счет появления множества признаков, обусловленных множеством световых потоков, реализующих WDM технологию в реальном времени.