ЭФФЕКТИВНЫЙ ЧИСЛЕННЫЙ МЕТОД РЕШЕНИЯ ЗАДАЧИ ФИШЕРА – КОЛМОГОРОВА-ПЕТРОВСКОГО-ПИСКУНОВА
ЭФФЕКТИВНЫЙ ЧИСЛЕННЫЙ МЕТОД РЕШЕНИЯ ЗАДАЧИ ФИШЕРА – КОЛМОГОРОВА-ПЕТРОВСКОГО-ПИСКУНОВА
Аннотация
Начально-краевая задача для квазилинейного уравнения реакции-диффузии Колмогорова-Петровского-Пискунова – Фишера служит математической моделью различных процессов и находит широкое применение в различных областях науки и техники. Удивительным свойством данного уравнения является существование разрывных решений, пропорциональных корню квадратному от произведения коэффициента диффузии на коэффициент при линейном источнике. В работе для численного решения начально-краевой задачи для одномерного квазилинейного уравнение Ф–КПП с граничными условиями Дирихле построена эффективная явно-неявная разностная схема. Приведены результаты численной реализации предложенной разностной схемы на модельной задаче с точным решением при разных значениях коэффициента диффузии и на разных пространственно-временных сетках. Они показали высокую ее эффективность, высокую точность определения решения и скорости «бегущей волны».
1. Введение
Уравнение Фишера–Колмогорова-Петровского-Пискунова(Ф-КПП) служит одной из классических моделей в математической биологии, экологии, горении, физике и химии. В 1937 г. А.Н.Колмогоров и его соавторы доказали существование и единственность решения начально-краевой задачи для квазилинейного параболического уравнения реакции-диффузии
. В ней авторы указали на применение данной задачи к математическому моделированию биологических процессов. Американский ученый Фишер в том же 1937 году опубликовал статью , в которой вывел дифференциальное уравнение описывающее спонтанный рост и распространение доминантного гена. В работах зарубежных ученых данное уравнение известно как уравнение Фишера. В 40-х годах Я.Б.Зельдович данную задачу использовал в качестве математической модели скорости распространения пламени по смеси (горение), реагирующей при начальной температуре, а также исследовал влияние начального условия на спонтанное распространение химической реакции (взрыв) , . J-Guy Caputo, B.Sarels в статье провели численный анализ взаимодействия фронта реакции-диффузии Зельдовича. L.K.Forbes в работе рассмотрел установившуюся модель реакции-диффузии для системы горения, в которой существуют конкурирующие пути эндотермической и экзотермической реакций. Некоторыми авторами были изучены содержательные обобщения этого уравнения. В статье Борисова А.В., Резаева Р.О. и др. было исследовано влияние нелокальных эффектов на динамику популяции микроорганизмов в рамках диффузионной модели с квадратично-нелинейным нелокальным взаимодействием, обобщающей известную модель Ф-КПП. В работе авторы представили численный метод аппроксимации численных решений нелинейного уравнения реакции-диффузии Фишера методом конечных разностей. Профессором Матусом П. были получены результаты по оценке устойчивости решений разностных схем для квазилинейного параболического уравнения и нелинейного уравнения переноса . В следующей работе Матуса П. построены и исследованы на устойчивость монотонные разностные схемы для уравнения Ф-КПП. Существует множество моделей динамики популяций, порождающих биологические волны. Мюррей и его соавторы выпустили книгу в двух томах «Математическая биология», посвященную биологическим волнам , . В монографии N.Bacaer описаны труды Фишера и Колмогорова. В них выведена формула для нахождения скорости распространения бегущей волны для уравнения Ф-КПП:В данной работе проводятся результаты вычислительного эксперимента о скорости распространения фронта волны для одномерного уравнения Ф-КПП. Для ее численного решения предложена разностная схема с явной аппроксимацией диффузионного члена. Обсуждаются результаты вычислительного эксперимента по определению фронта «бегущей волны» для одномерного квазилинейного уравнения реакции-диффузии. Во введении приведен обзор литературы, посвященной численной реализации модели Ф-КПП. Во втором разделе представлена постановка задачи. В третьем разделе предложен численный метод решения поставленной задачи, заключающийся в явной аппроксимации диффузионного члена. В четвертом разделе обсуждаются результаты вычислительного эксперимента при различных значениях входных параметров модели. Кроме того, был проведен вычислительный эксперимент по нахождению скорости фронта бегущей волны.
2. Постановка задачи
Рассмотрим начально-краевую задачу для одномерного квазилинейного уравнения Ф-КПП:
где – время,
– пространственные координаты,
– коэффициент диффузии,
– коэффициент прироста бактерий,
– коэффициент конкурентных потерь, называемый функцией влияния,
– искомая кинетическая переменная.
Задаем однородные граничные условия Дирихле:
Задается начальное условие:
Для установления точности разностной схемы проведем сравнение с точным решением при :
3. Разностная схема
Поставленную задачу решаем с помощью метода конечных разностей. В области определения поставленной задачи (1)-(3) введем прямоугольную пространственно-временную сетку с постоянными шагами
и
:
На построенной прямоугольной пространственно-временной сетке задаче (1) - (3) поставим в соответствие следующую явно-неявную разностную схему:
Отметим, что разностная схема (8) построена таким образом, что диффузионный член аппроксимирован явно, остальные слагаемые аппроксимированы со вторым порядком по времени. Учитывая малость коэффициента диффузии для практических задач можем расчеты проводить с достаточно большим временным шагом.
Решение разностной схемы (8) при сходится к решению дифференциальной задачи (1) - (3) при выполнении условия устойчивости со скоростью порядка
.
Для нахождения скорости движущегося фронта используем формулу взятую из монографии
:4. Вычислительный эксперимент
В этом разделе мы проводим численный эксперимент модельной задачи с помощью явно-неявной разностной схемы. При заданном значении финального времени пространственная шкала
регулируется таким образом, чтобы бегущие волны не достигают границ области определения задачи. Численная реализация разностной схемы (8) проведена на языке Python.
Вычислительный расчет одномерного уравнения Ф-КПП проводились при следующих значениях исходных данных и параметров сетки . На рис. 1 представлены графики результатов точного и численного решения в разные моменты времени:
. На данном рисунке начальное условие представлено голубым цветом, а точное решение отмечено черным контуром. Результаты вычислений представлены графически таким образом, чтобы численный результат можно было сравнить с точным решением. Полученные результаты соответствуют с точным решением, а постоянная скорость движения "бегущей волны" определяется с высокой точностью.
На рис. 2 представлены графики абсолютной ошибки в разные моменты времени: . Из представленных графиков ошибка между решениями достаточно маленькое. C ростом времени ошибка несущественно растет. На выбранных значениях исходных данных возможно применить данную задачу на грубой сетке с хорошей точностью.
На рис. 3 представлена скорость распространения бегущей волны. Как видно из графика в малое время (в начальном моменте времени) имеется маленькая погрешность, а далее скорость фронта движется линейно с постоянной скоростью. Прогнозируемая скорость волны .
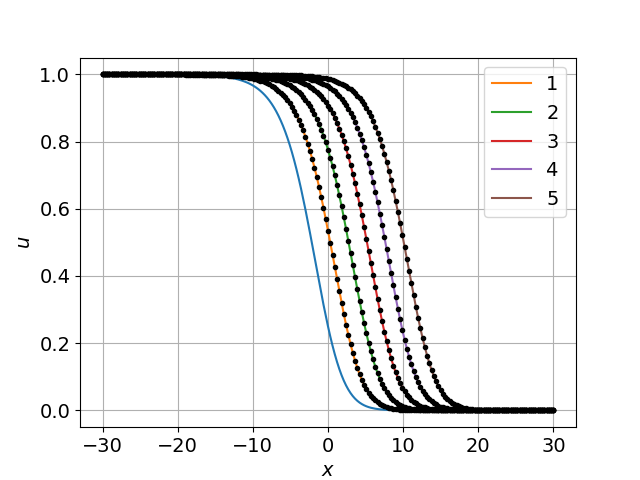
Рисунок 1 - Численное и точное решение в разные моменты времени при D=1
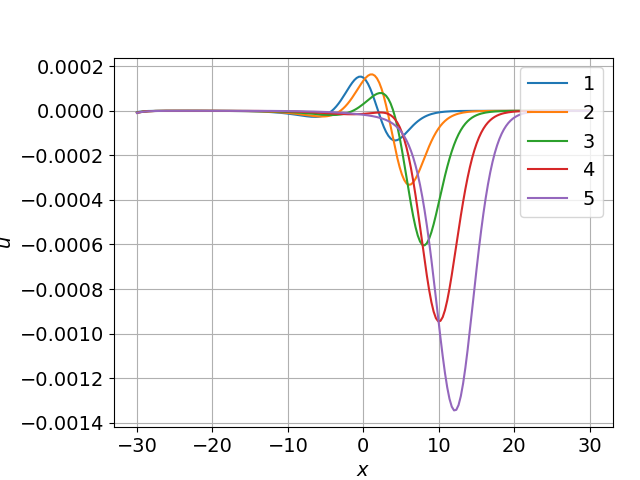
Рисунок 2 - Разница численных решений при D=1
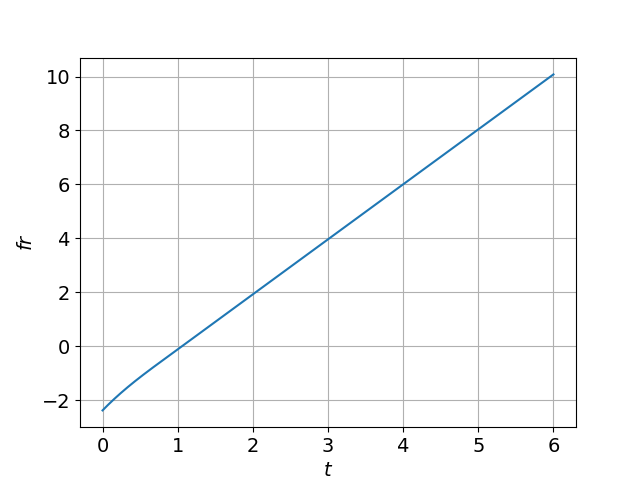
Рисунок 3 - Динамика распространения бегущей волны при D=1
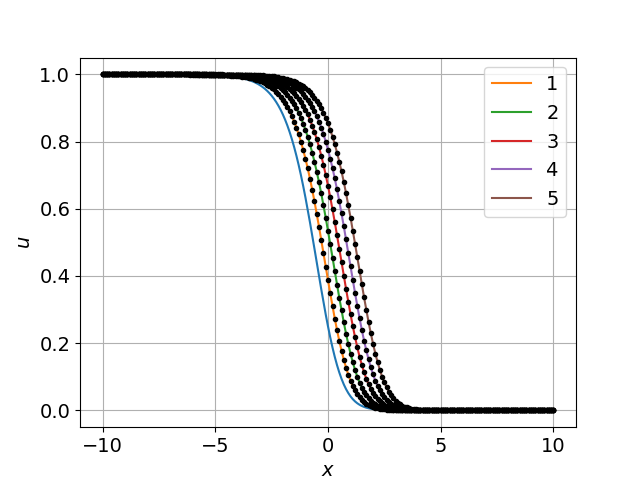
Рисунок 4 - Численное и точное решение в разные моменты времени при D=0,09
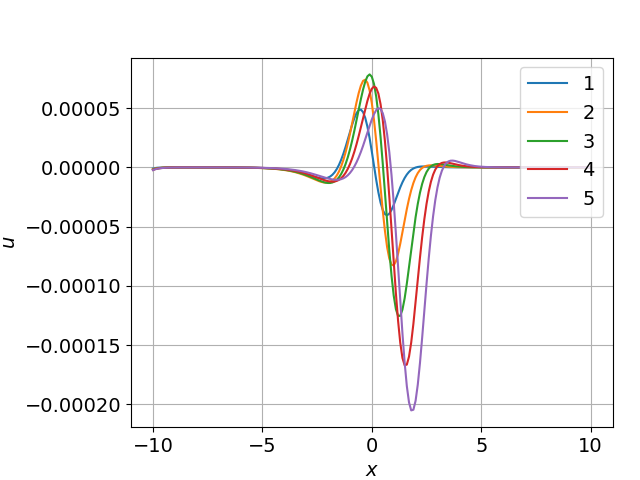
Рисунок 5 - Разница численных решений при D=0,09
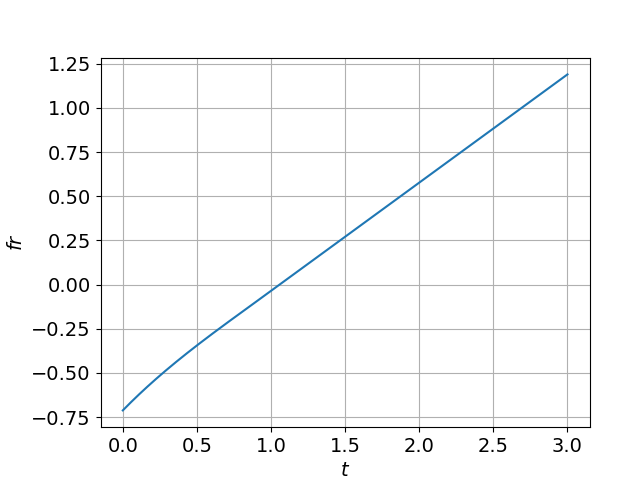
Рисунок 6 - Динамика распространения бегущей волны при D=0,09
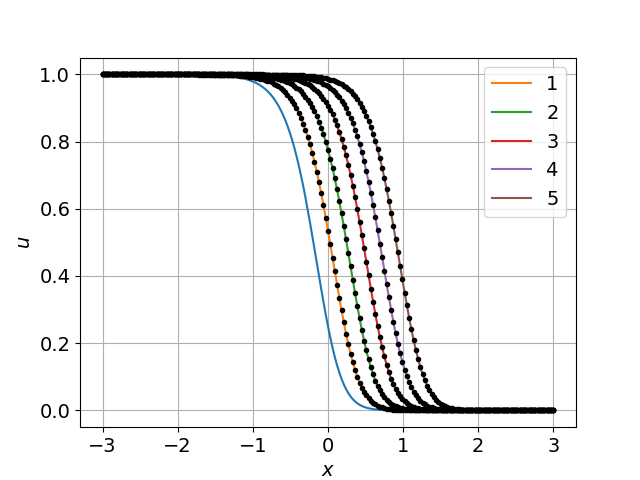
Рисунок 7 - Численное и точное решение в разные моменты времени при D=0,0081
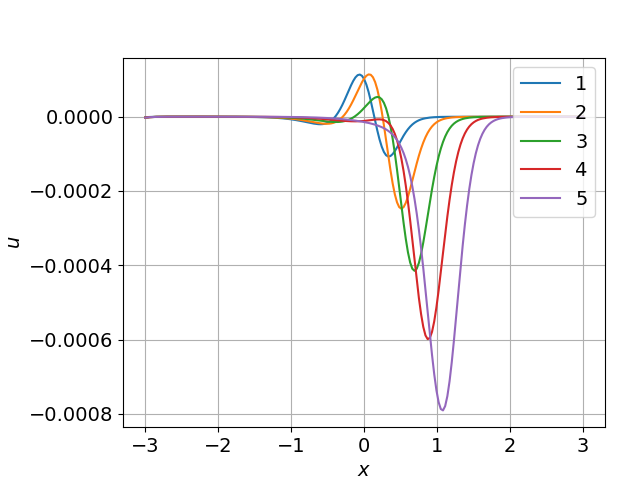
Рисунок 8 - Разница численных решений при D=0,0081
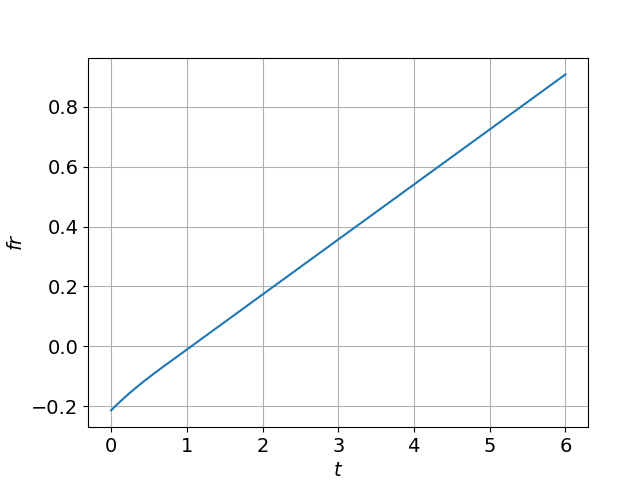
Рисунок 9 - Скорость распространения бегущей волны при D=0,0081
Таблица 1 - Сравнение ошибки в разные моменты времени на двух значениях шага пространственной сетки и четырех значениях шага временной сетки в разные моменты времени
J | Errort1 | Errort2 | Errort3 | Errort4 | Errort5 |
N=100 | |||||
150 | 0,0005411 | 0,0010736 | 0,0019090 | 0,0029216 | 0,0041059 |
300 | 0,0002834 | 0,0006089 | 0,0009289 | 0,0012197 | 0,0014390 |
600 | 0,0002418 | 0,0004325 | 0,0005034 | 0,0004145 | 0,0003781 |
1 200 | 0,0002384 | 0,0003770 | 0,0003389 | 0,0005069 | 0,0008668 |
N=200 | |||||
150 | 0,0005426 | 0,0010883 | 0,0020892 | 0,0034469 | 0,0051525 |
300 | 0,0002588 | 0,0005496 | 0,0010325 | 0,0016717 | 0,0024498 |
600 | 0,0001284 | 0,0002791 | 0,0004969 | 0,0007636 | 0,0010676 |
1 200 | 7,2647e-05 | 1,5565e-04 | 2,3858e-04 | 3,1342e-04 | 3,7424e-04 |
5. Заключение
В работе для численного решения начально-краевой задачи для квазилинейного уравнения Ф–КПП предложена эффективная разностная схема с явной аппроксимацией диффузионного члена и аппроксимацией остальных слагаемых уравнения со вторым порядком по времени. Приведены результаты ее численной реализации на модельном примере с точным решением типа «бегущей волны». Расчеты показали высокую точность предложенной разностной схемы.
