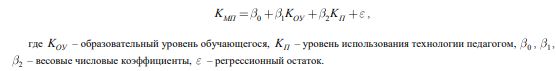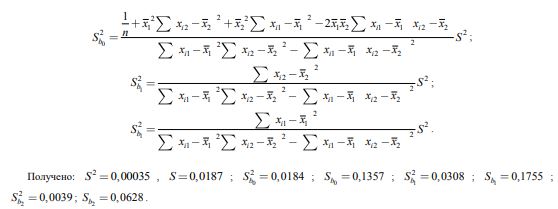ОЦЕНКА ЭФФЕКТИВНОСТИ ТЕХНОЛОГИИ ИНТЕРАКТИВНОГО ОБУЧЕНИЯ МАТЕМАТИКЕ

ОЦЕНКА ЭФФЕКТИВНОСТИ ТЕХНОЛОГИИ ИНТЕРАКТИВНОГО ОБУЧЕНИЯ МАТЕМАТИКЕ

Научная статья

Сиротина И.К.^*

Ленинградский государственный университет имени А.С. Пушкина, Санкт-Петербург, Россия

* Корреспондирующий автор (i_sirotina[at]mail.ru)

Аннотация

В статье с помощью методов математической статистики на основании анализа экспериментальных данных приводится проверка эффективности технологии интерактивного обучения математике, которая устанавливается с помощью показателя «Целевая функция качества», количественно оцениваемого коэффициентом уровня математической подготовки обучающихся. Тест Чоу показал, что мы не можем построить общее уравнение регрессии для экспериментального и контрольного классов. Уравнения регрессий отличаются средней оценкой влияния технологии обучения на уровень математической подготовки обучающегося, которое в экспериментальном классе значительно выше, чем в контрольном. Полученные экспериментально результаты исследования показывают, что разработанная нами технология интерактивного обучения математике на этапе функционирования удовлетворяет критерию продуктивности.

Ключевые слова: математика, интерактивное обучение, технология, эффективность, уравнение регрессии, гипотеза, автокорреляция, гетероскедастичность, ранговая корреляция.

AN EVALUATION OF THE EFFECTIVENESS OF INTERACTIVE MATHEMATICS TEACHING TECHNOLOGY

Research article

Sirotina I.K.^*

Pushkin Leningrad State University, Saint Petersburg, Russia

* Corresponding author (i_sirotina[at]mail.ru)

Abstract

The article uses methods of mathematical statistics based on the analysis of experimental data to verify the effectiveness of the interactive technology for teaching mathematics, which is established using the indicator "Objective function of quality" quantified by the coefficient of the level of mathematical training of students. The Chow test showed that there is no possibility of constructing a general regression equation for the experimental and control classes. Regression equations differ in the average assessment of the impact of learning technology on the level of mathematical training of students, which is significantly higher in the experimental class than in the control one. The experimental results of the study show that the developed technology of interactive teaching of mathematics satisfies the criterion of productivity at the stage of functioning.

Keywords: mathematics, interactive learning, technology, efficiency, regression equation, hypothesis, autocorrelation, heteroscedasticity, rank correlation.

Введение

Под технологией обучения понимают способ воспроизведения положительного педагогического результата, диагностично заданного нормами обучающих и управляющих программ, в условиях, адекватных целям образования [1, С. 441]. Педагогическая технология, как и всякая другая технология, предполагает получение запрограммированного на этапе ее проектирования продукта [2] и требует оценки эффективности на этапе ее функционирования. Выявление влияния технологии обучения на уровень подготовки обучающихся осуществляется как правило в результате педагогического эксперимента и требует использования комплекса методов математической статистики. Оценка эффективности, разработанной нами технологии интерактивного обучения математике, проводится на основании данных педагогического эксперимента (10 – 11 классы) по критерию продуктивности [3] на основании таких показателей как образовательный уровень обучающегося и уровень использования технологии педагогом.

Построение эмпирического уравнения регрессии

Главную целевую функцию качества образовательного процесса (формирование математической культуры личности как целостности), количественно оцениваемую коэффициентом  уровня математической подготовки обучающегося, представим в виде:

Таблица 1 – Промежуточные расчеты для уравнения (1)

	октябрь	ноябрь	декабрь	январь	февраль	март	апрель	май
	0,542	0,596	0,629	0,675	0,738	0,758	0,786	0,8
	–0,149	–0,095	–0,062	–0,016	0,047	0,067	0,095	0,109
	0,0222	0,009	0,0038	0,0003	0,0022	0,0045	0,009	0,0119
	0,574	0,602	0,662	0,699	0,750	0,819	0,758	0,788
	–0,133	–0,105	–0,045	–0,008	0,043	0,112	0,051	0,081
	0,0177	0,0110	0,0020	0,0000	0,0018	0,0125	0,0026	0,0066
	0,166	0,237	0,339	0,423	0,529	0,623	0,733	0,814
	–0,317	–0,246	–0,144	–0,060	0,046	0,140	0,250	0,331
	0,1005	0,0605	0,0207	0,036	0,0021	0,0196	0,0625	0,1095
	0,5600	0,5881	0,6401	0,6757	0,7232	0,7791	0,7618	0,7928
е	0,018	–0,0075	0,0111	0,0007	–0,0148	0,0211	0,0242	0,0072
	0,00032	0,00006	0,00012	0,00000	0,00022	0,00044	0,00058	0,00005
		0,00065	0,00035	0,00011	0,00024	0,00129	0,00001	0,00099

Получено: 1 b 0,5833 ; 2 b 0,1667 ; 0 b 0,5794. Дисперсии и стандартные ошибки коэффициентов рассчитаны по формулам пособия [7]:

Коэффициент регрессии  b₁ при переменной K_oy  равен 0,5833. Это свидетельствует, что рост образовательного уровня обучаемого улучшает качество его математической подготовки. Установлена статистическая значимость этого коэффициента. Для этого на основе t-статистики  проверена гипотеза: H₀: B₁=0 при конкурирующей гипотезе то данный коэффициент статистически значим. Это подтверждает положительную зависимость между начальным образовательным уровнем обучаемого и ожидаемым уровнем его математической подготовки.

Коэффициент регрессии  при переменной  равен 0,1667. Установлена статистическая значимость этого коэффициента. На основе t-статистики  проверена гипотеза  при конкурирующей гипотезе . Так как , то данный коэффициент статистически значим. Это подтверждает положительную зависимость между педагогической технологией и математической подготовкой обучающегося.

Доверительные интервалы коэффициентов регрессии [6] рассчитаны по формуле: . С учетом , получено:

Так как ни один их интервалов не содержит нулевого значения, то это подтверждает гипотезу о статистической значимости всех коэффициентов.

Коэффициент детерминации [7] рассчитан по формуле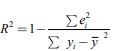 , откуда R₂=0?9714. Коэффициент детерминации указывает на то, что модель объясняет 97,14% отклонений зависимой переменной. Статистическая значимость коэффициента детерминации проверена с помощью гипотезы H₀: R²  =0 при H₁: R²>0. С помощью статистики Фишера  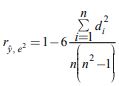найдено . При уровне значимости  найдено критическое значение распределения Фишера: . Так как , то нулевая гипотеза отклонена, следовательно, коэффициент детерминации статистически значим, и модель имеет хорошее общее качество. Гипотеза об отсутствии автокорреляции[7] проверена на основе статистики Дарбина–Уотсона DW, которая определена по формуле . Получено: DW=2,02. Для  найдены критические точки распределения Дарбина – Уотсона  d₁= 0, 359 и du= 1, 777. Так как выполняется условие , 1,177 <DW<2,223, то автокорреляция остатков отсутствует. Отсутствие гетероскедастичности (непостоянства дисперсии отклонений) установлена с помощью ранговой корреляции Спирмена [6]. Гипотезы: :   (гетероскедастичность отсутствует); . Коэффициент ранговой корреляции [7] найден по формуле:  , где d₁ – разность между рангами  и ; n – число наблюдений. Получено:  (Таблица 2).

Таблица 2 – Промежуточные расчеты для 

	0,5600	0,5881	0,6401	0,6757	0,7232	0,7618	0,7791	0,7928
	0,00032	0,00006	0,00012	0,00000	0,00022	0,00058	0,00044	0,00005
rank	6	3	4	1	5	8	7	2
	–5	–1	–1	3	0	–2	0	6

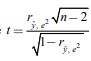По формуле  найдено наблюдаемое значение t-статистики: t_n=0, 2451 . По таблице критических точек распределения Стьюдента найдено  . Так как , то принимается основная гипотеза. Следовательно, гетероскедастичность по критерию Спирмена не подтверждается. Следовательно, построенная модель имеет высокое общее качество и вполне пригодна для анализа поведения переменной Y=K_мп и прогноза ее значений.

По результатам обучающего эксперимента в контрольном классе (Таблица 3) получено уравнение регрессии:

Таблица 3 – Промежуточные расчеты для уравнения (2)

	октябрь	ноябрь	декабрь	январь	февраль	март	апрель	май
	0,6118	0,6294	0,6647	0,6941	0,7118	0,7059	0,7059	0,7294
	–0,0698	–0,0522	–0,0169	0,0125	0,0302	0,0243	0,0243	0,0478
	0,0049	0,0027	0,0003	0,0002	0,0009	0,0006	0,0006	0,0023
	0,6324	0,6797	0,6993	0,6647	0,7712	0,7908	0,7059	0,7843
	–0,0836	–0,0363	–0,0167	–0,0513	0,0552	0,0746	–0,0101	0,0683
	0,0070	0,0013	0,0003	0,0026	0,0030	0,0056	0,0001	0,0047
	0,165	0,250	0,325	0,424	0,480	0,524	0,585	0,610
	–0,2554	–0,1704	–0,0954	0,0036	0,0596	0,1036	0,1646	0,1896
	0,0652	0,0290	0,0091	0,00001	0,0036	0,0107	0,0271	0,0359
	0,6118	0,6294	0,6647	0,6941	0,7118	0,7059	0,7059	0,7294
	0,6306	0,4524	0,6637	0,6614	0,6970	0,7062	0,6841	0,7103
е	0,0188	0,023	–0,001	–0,0326	–0,0142	0,0003	–0,0218	–0,0191
	0,00035	0,00005	0,000001	0,00107	0,00022	0,0000	0,00047	0,00036
		0,00065	0,00035	0,00011	0,00024	0,00129	0,00001	0,00099

Коэффициент детерминации R²=0, 7984 указывает на то, что модель объясняет 79,84% отклонений зависимой переменной. Статистическая значимость коэффициента детерминации проверена с помощью гипотезы  при . С помощью статистики Фишера найдено . При уровне значимости  найдено критическое значение распределения Фишера: то нулевая гипотеза отклонена, следовательно, коэффициент детерминации статистически значим, и модель имеет хорошее общее качество.

Проверка гипотезы о совпадении уравнений регрессий (1) и (2)

С помощью теста Чоу [8] проверена гипотеза о совпадении уравнений регрессии для экспериментальной и контрольной групп. По объединенной выборке  экспериментального и контрольного классов (Таблица 4) получено третье уравнение регрессии:

(3)

Таблица 4 – Промежуточные расчеты для уравнения (3)

	0,5707	0,6098	0,6439	0,6829	0,7268	0,7366	0,7536	0,7707
	–0,1162	–0,0773	–0,043	–0,004	0,0399	0,0497	0,0667	0,0838
	0,0135	0,0060	0,0018	0,00002	0,0016	0,0025	0,0044	0,0070
	0,5691	0,6341	0,6775	0,6439	0,7588	0,8075	0,7366	0,7536
	–0,1285	–0,0635	–0,0201	–0,0537	0,0612	0,1095	0,0390	0,0560
	0,1665	0,0040	0,0004	0,0029	0,0037	0,0121	0,0015	0,0031
	0,1655	0,2435	0,332	0,4235	0,5045	0,5735	0,6590	0,0712
	–0,2862	–0,2082	–0,1197	–0,0282	0,0528	0,1218	0,2073	0,2603
	0,0819	0,0433	0,0143	0,0008	0,0028	0,0148	0,0430	0,0678
	0,5707	0,6098	0,6439	0,6829	0,7268	0,7366	0,7536	0,7707
	0,7262	0,7181	0,7063	0,6870	0,6829	0,6751	0,6534	0,6455
	0,0242	0,0117	0,0039	0,00002	0,0019	0,00003	0,0100	0,0157

Заключение

Полученные экспериментально результаты исследования показывают, что разработанная нами технология интерактивного обучения математике на этапе функционирования обеспечивает продуктивный процесс формирования математической культуры личности и повышает уровень математического образования обучающихся. Технология может быть применена на любом этапе обучения, но с учетом возрастных особенностей обучающихся.

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. 1. Романцев Г. М. Профессионально-педагогические понятия: Слов. / Г. М. Романцев, В. А. Федоров, И. В.Осипова и др.; Под ред. Г.М. Романцева. – Екатеринбург: Изд-во Рос. гос. проф.-пед. ун-та, 2005. – 456 с.
2. Пластинина, Ю. Л. Продуктивная учебная деятельность в образовательном пространстве школы / Ю. Л. Пластинина // Вектор науки ТГУ. №1(8), 2012. – С. 240 – 243.
3. Сиротина, И. К. Разработка диагностического компонента образовательной технологии / И.К. Сиротина // Международный научно-исследовательский журнал. – № 4 (106) 2021 Часть 3 Апрель. – С. 116 – 118.
4. Ерунов, В. П. Оценка эффективности функционирования образовательного процесса в вузе / В. П. Ерунов, О. С. Бравичева // Вестник ОГУ. – 2005. – № 10. – Том 1. – С. 191–197.
5. Сиротина, И. К. Методика расчета технологического коэффициента преподавателя математики / И.К. Сиротина // Проблемы управления качеством образования: сборник избранных статей Международной научно-методической конференции (Санкт-Петербург, Март 2021). – СПб.: ГНИИ «Нацразвитие», 2021. – С. 53 – 56.
6. Гмурман, В. Е. Теория вероятностей и математическая статистика: учеб. пособие для вузов / В.Е. Гмурман. – 9-е изд. – М: Высш. шк., 2003. – 479с.
7. Бородич, С. А. Эконометрика. Практикум : учеб. пособие / С. А. Бородич. – Минск : Новое знание; М. : ИНФРА-М, 2014. – 329 с.
8. Булдык, Г. М. Экономико-математическое моделирование как усиление практико-ориентированной направленности математической культуры студентов экономических специальностей / Г. М. Булдык //Весцi БДПУ Сер. 3. – 2013. – № 2. – С. 32–37. 9. Середенко, П. В. Методы математической статистики в психолого-педагогических исследованиях: учеб. пособ. / П.В. Середенко, А.В. Должикова. – 2-е изд.. –Южно-Сахалинск: СахГУ, 2009. – 52 с.

Список литературы на английском языке / References in English

1. Professional'no-pedagogicheskie ponjatija: Slov [Professional and pedagogical concepts: Words] / G. M. Romantsev, V. A. Fedorov, I. V.Osipova, et al; Edited by G.M. Romantsev. - Yekaterinburg: Publishing House of the Russian State Professional Pedagogical University, 2005– 456 p. [in Russian]
2. Plastinina, Y. L. Produktivnaja uchebnaja dejatel'nost' v obrazovatel'nom prostranstve shkoly [Productive educational activity in the educational space of the school] / Yu. L. Plastinina // Vektor nauki TGU [Vector of Science TSU]. №1(8), 2012. – Pp. 240 - 243 [in Russian]
3. Sirotina, I. K. Razrabotka diagnosticheskogo komponenta obrazovatel'nojj tekhnologii [Development of the diagnostic component of educational technology] / I.K. Sirotina // Mezhdunarodnyjj nauchno-issledovatel'skijj zhurnal [International Research Journal]. - No. 4 (106) 2021 Part 3 April. - pp. 116 - 118 [in Russian]
4. Yerunov, V. P. Ocenka ehffektivnosti funkcionirovanija obrazovatel'nogo processa v vuze [Evaluation of the effectiveness of the functioning of the educational process at the university] / V. P. Yerunov, O. S. Bravicheva // Vestnik OGU [Bulletin of OSU]. - 2005. - No. 10. - Volume 1. - pp. 191-197 [in Russian]
5. Sirotina, I. K. Metodika rascheta tekhnologicheskogo koehfficienta prepodavatelja matematiki [Methodology for calculating the technological coefficient of a mathematics teacher] / I.K. Sirotina // Problemy upravlenija kachestvom obrazovanija: sbornik izbrannykh statejj Mezhdunarodnojj nauchno-metodicheskojj konferencii (Sankt-Peterburg, Mart 2021) [Problems of quality management of education: a collection of selected articles of the International Scientific and Methodological Conference (St. Petersburg, March 2021)]. - St. Petersburg: GNII "National Development", 2021. - pp. 53-56 [in Russian]
6. Gmurman, V. E. Teorija verojatnostejj i matematicheskaja statistika: ucheb. posobie dlja vuzov [Probability theory and mathematical statistics: studies. handbook for universities] / V.E. Gmurman. - 9th ed. - Moscow: Vysshaya shkola, 2003. - 479 p. [in Russian]
7. Borodich, S. A. Ehkonometrika. Praktikum : ucheb. posobie [Econometrics. Workshop : study. manual] / S. A. Borodich. - Minsk : Novoe Znanie; Moscow : INFRA-M, 2014. - 329 p. [in Russian]
8. Buldyk, G. M. Ehkonomiko-matematicheskoe modelirovanie kak usilenie praktiko-orientirovannojj napravlennosti matematicheskojj kul'tury studentov ehkonomicheskikh special'nostejj [Economic and mathematical modeling as strengthening of practice-oriented orientation of mathematical culture of students of economic specialties] / G. M. Buldyk // Vesci BDPU [Bulletin of BDPU] Ser. 3. – 2013. – № 2. – Pp. 32-37 [in Russian]
9. Seredenko, P. V. Metody matematicheskojj statistiki v psikhologo-pedagogicheskikh issledovanijakh: ucheb. posob. [Methods of mathematical statistics in psychological and pedagogical research: a manual] / P.V. Seredenko, A.V. Dolzhikova. - 2nd ed.. - Yuzhno-Sakhalinsk: Sakhalin State University, 2009. - 52 p. [in Russian]