АДАПТАЦИОННАЯ СОСТАВЛЯЮЩАЯ ПРИ ОБУЧЕНИИ ПЕРВОКУРСНИКОВ МАТЕМАТИКЕ

Гришкина Т.Е.¹, Лебедь О.А.², Павельчук А.В.³

¹Старший преподаватель, ²старший преподаватель, ³ассистент, Амурский государственный университет

АДАПТАЦИОННАЯ СОСТАВЛЯЮЩАЯ ПРИ ОБУЧЕНИИ ПЕРВОКУРСНИКОВ МАТЕМАТИКЕ

Аннотация

В статье рассмотрена  адаптационная составляющая при обучении математике студентов первого курса. Обоснована целесообразность введения адаптивного курса математики, раскрыты его основные содержательные моменты.

Ключевые слова: адаптация, учебная адаптация, адаптационная подготовка, адаптивный курс математики.

Grishkina TE¹, Lebed OA², Pavelchuk AV³

¹Senior Lecturer; ²Senior Lecturer, ³assistant, Amur State University

ADAPTIVE COMPONENT IN MATHEMATICS EDUCATION  FIRST-YEAR STUDENTS

Abstract

In this article the adaptive component of teaching mathematics first year students. The expediency of introducing adaptive mathematics course offered, its main points.

Keywords: adaptation, learning adaptation, adaptive training, adaptive mathematics course.

Высшее образование для молодого человека – это та ступень  профессионального становления, на которой он должен получить мощный толчок к развитию своего интеллектуального потенциала, стимулированию процессов саморазвития и самообразования,  к активному формированию познавательных и профессиональных навыков.

Однако, в последние годы выпускники школ не готовы к освоению программ высшего профессионального образования. Для многих абитуриентов характерны репродуктивно-подражательный уровень познавательной активности, слабое владение приемами самостоятельной, исследовательской деятельности, интеллектуальными и учебными умениями, недостаточная мотивация к учебе, избранной профессии. Поэтому вузы обращают свое внимание не только на качество подготовки абитуриентов, но и на адаптацию первокурсников к образовательному процессу, к социокультурной  образовательной среде.

Различные аспекты проблемы адаптации выпускников школ в учебных заведениях рассмотрены в исследованиях Ю.А. Александровского, В.А. Зозули, Д.А. Ловцова, В.В.Богорева, В.Ф. Романченко, З.Г. Клименко, В.И. Егорова, Н.С. Аболиной, О.В. Гилевой, О.И. Спесивцевой.

В различных определениях сущности адаптации можно выделить два подхода. Первый – «адаптация» понимается как пассивное приспособление, привыкание к новой среде. Второе – это процесс активного усвоения студентами всех условий новой деятельности. В социологии адаптацией называют не просто процесс приспособления личности к определенным условиям, но и процесс, в котором личность играет активную роль в жизни коллектива.

А.В. Степанов выделяет адаптированные качества личности: «потребность в постоянном пополнении своих знаний, в самообразовании; достаточно высокая обучаемость, сочетающаяся с установкой на преодоление трудностей в процессе познания; склонность к работе исследовательского характера; коммуникабельность, то есть способность к общению, быстрому образованию эмоциональных контактов с людьми, общительность; творческое отношение к своей деятельности» [1].

А.В. Кажин, Л.Н. Еговцева, Н.Г. Качалова дают следующее определение адаптации первокурсников, это «…есть процесс их перехода от маргинальности к состоянию относительной социальной и психологической стабильности» [2].

Адаптация с педагогической точки зрения рассматривается как комплексный процесс, включающий биологическую, физиологическую и социально-психологическую адаптацию, как процесс активного взаимодействия личности со средой, где происходит не только адаптация к успешному функционированию в данной среде, но и активное освоение предметного пространства.

Адаптация первокурсников в вузе определяется как процесс приспособления студентов к учебному процессу: новой структуре (новым формам, методам учебной деятельности), к новой социальной среде - учебный коллектив вуза (студенческой группы, коллективу преподавателей), к изучению математики и других учебных предметов. Применительно к первокурсникам рассматриваются две ее стороны - социально-психологическая и учебная.

Организация адаптации первокурсников на уровне вуза еще не носит системного характера, часто сводится к «точечным», «ситуационным» влияниям на  процесс личностного развития, при этом приоритетными являются вопросы социальной адаптации.

Проблема социально-психологической адаптации студентов к обучению в вузе уже исследована в работах ряда авторов [3,4].  Авторами предлагались методики довузовской подготовки. В них показано, что от степени готовности первокурсников к обучению в вузе зависит и успешность их последующего обучения.

Что касается  учебной адаптации, то она осуществляется в основном на энтузиазме преподавателей. Обнаруживая неготовность студентов к освоению их учебных курсов, они обобщают и систематизируют соответствующие школьные знания, доводят до необходимого уровня умения и навыки учебной деятельности.

По нашему мнению, именно данная адаптация является наиболее проблемной, именно она должна стать тем необходимым условием, которое позволит первокурснику наиболее успешно включиться в качественно новый образовательный процесс в вузе.

Существующие противоречия между требованиями вузов к уровню математической подготовки первокурсников и реальным ее состоянием  помогла бы решить математическая адаптационная подготовка первокурсников.

Адаптационная подготовка первокурсников по математике в нашем понимании - это  процесс их учебной адаптации, снимающий трудности, связанные с изучением математики в вузе.

Создание адаптивного курса математики для студентов первого курса, который бы приводил в систему знания по математике, полученные раннее, является одним из возможных путей реализации на практике адаптационной подготовки.

В вузе разработаны несколько адаптивных курсов по математике для студентов различных специальностей. Данные курсы изучаются студентами параллельно с курсом математики в течение первого семестра обучения.

Рассмотрим более подробно один из них  (для студентов экономических специальностей). Курс содержит следующие разделы: преобразование алгебраических выражений; алгебраические уравнения, системы и неравенства; показательные, логарифмические уравнения и неравенства; тригонометрия; производная функции и некоторые её приложения.

Сопоставление курсов математики в школе и в вузе позволило выделить основные содержательные линии школьного курса математики, которые наиболее близки к вузовскому  и  вынести некоторые темы на рассмотрение в адаптивный курс.

Например, в школьном курсе математике рассматриваются следующие задачи по теме производная функции:

Найти производную функции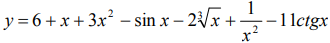

Решение:

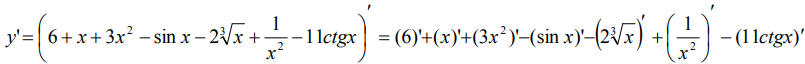
Для дифференцирования все корни, степени нужно представить в виде 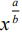, а если они находятся в знаменателе, то переместить их в числитель.

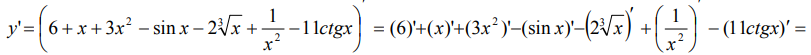
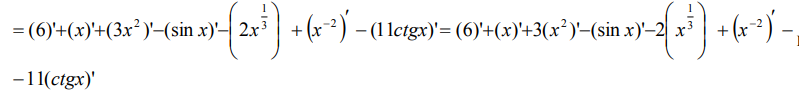
Все функции, находящиеся под штрихами, являются элементарными табличными функциями.

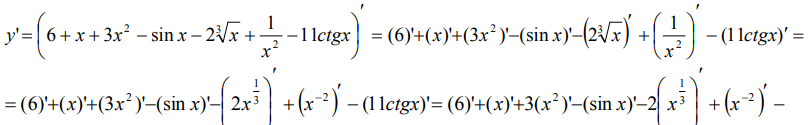
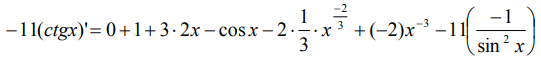
Так как штрихов больше нет ‑ производная найдена.

В адаптивном курсе мы расширяем понятие производной. Подробно рассматриваем темы: производная высших порядков, применение производной при анализе функций и др. Например:

Найти вторую производную функции .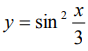

Найдем первую производную:

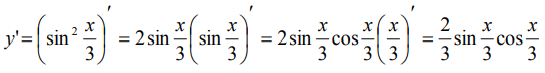
На этом шаге смотрим, нельзя ли что-нибудь упростить? Используем формулу :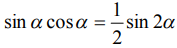

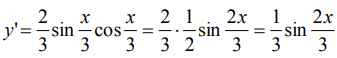
Находим вторую производную:

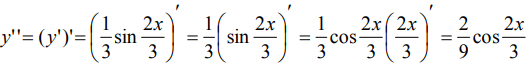
Можно было решить другим способом – понизить степень функции еще перед дифференцированием, используя формулу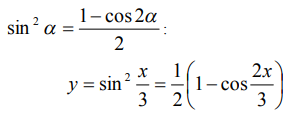

Далее взять первую и вторую производные. Результаты, естественно, совпадут.

Таким образом, переход от школьной математики к вузовской для студентов первого курса осуществляется более эффективно.

В адаптивный курс следует включать темы и разделы, которые студенты повторяют и изучают самостоятельно более углубленно (например: алгебраические уравнения, системы и неравенства).

Мы рекомендуем, в рамках адаптивного курса, привлекать студентов к написанию рефератов, выпуску математических газет, математических кроссвордов, составлению тестов - это активизирует их мысль, организует, стимулирует применение базовых знаний на практике и способствует глубокому усвоению материала. У студентов, ранее не любивших математику в силу её незнания и непонимания в школе, появляется к ней устойчивый интерес, желание достигнуть успеха в различных видах деятельности, что, как следствие, приводит к знанию предмета.

Применение адаптивного подхода при изучении математики первокурсниками способствует закреплению и систематизации базовых знаний полученных в школе, позволяет значительно повысить эффективность освоения математики в вузе.

Литература

1. Степанов А.В. Концепция адаптации как одна из теоретических основ организации исследований по проблеме преемственности учебно-воспитательного процессе в школе и в вузе / А.В. Степанов //Преемственность педвуза и школы в подготовке будущего учителя сб.науч.труд. – Йошкар – Ола: МГПИ, 1991 – С.5–9.

2. Кажин А.В. Управление процессом адаптации студентов: структура, формы и методы. Тезисы докладов Всероссийской научнопрактической конференции. Том 2 / А.В. Кажин, Л.Н. Еговцева, Н.Г.Качалова. – Екатеринбург: ГОУ УГТУ-УПИ, 2002. – С. 98 – 102.

3. Вопросы преподавания алгебры и начал анализа в средней школе: Сборник статей. Составители Глаголева Е.Г., ИвашевМусатов О.С. М.: Просвещение, 1980. – 256 с.

4. Дорофеев Г.В. Непрерывный курс математики в школе и проблема преемственности // Математика в школе. 1998. – №5. – с.70.