ИССЛЕДОВАНИЕ ОБРАТНОЙ КРАЕВОЙ ЗАДАЧИ АЭРОГИДРОДИНАМИКИ В МОДИФИЦИРОВАННОЙ ПОСТАНОВКЕ

ИССЛЕДОВАНИЕ ОБРАТНОЙ КРАЕВОЙ ЗАДАЧИ АЭРОГИДРОДИНАМИКИ В МОДИФИЦИРОВАННОЙ ПОСТАНОВКЕ

Научная статья

Салимов Р.Б.¹, Горская Т.Ю.^2, *

¹ ORCID: 0000-0003-4177-4830;

² ORCID: 0000-0001-7136-8388;

^{1, 2} Казанский государственный архитектурно-строительный университет, Казань, Россия

* Корреспондирующий автор (gorskaya0304[at]mail.ru)

Аннотация

Рассматривается видоизмененная обратная краевая задача аэрогидродинамики, в которой требуется найти форму крылового профиля, обтекаемого потенциальным потоком несжимаемой невязкой жидкости, когда распределение  потенциала скорости на одном участке профиля задано как функция абсциссы, на остальном участке профиля – как функция ординаты точки профиля, кроме того, задана величина скорости набегающего потока.

Ключевые слова: обратная смешанная краевая задача, аэрогидродинамика, крыловой профиль, комплексный потенциал.

RESEARCH OF REVERSE BOUNDARY VALUE PROBLEM OF AEROHYDRODYNAMICS IN MODIFIED STATEMENT

Research article

Salimov R.B.¹, Gorskaya T.Yu.^2, *

¹ ORCID: 0000-0003-4177-4830;

² ORCID: 0000-0001-7136-8388;

^{1, 2} Kazan State University of Architecture and Engineering, Kazan, Russia

* Corresponding author (gorskaya0304[at]mail.ru)

Abstract

In this paper, the authors consider a modified inverse boundary-value problem of aerohydrodynamics, in which it is necessary to find the shape of a wing profile streamlined by a potential flow of an incompressible inviscid fluid when the distribution of the velocity potential in one section of the profile is specified as a function of the abscissa, in the rest of the profile as a function of the ordinate of the profile point, in addition, value of speed of a free stream.

Keywords: inverse mixed boundary value problem, aerohydrodynamics, wing profile, integrated potential. 

Введение. Постановка задачи

Пусть в плоскости комплексного переменного z = x + iy расположен крыловой профиль L_z, обтекаемый потенциальным потоком несжимаемой невязкой жидкости с комплексным потенциалом w = w(z) = φ + iψ  и скоростью невозмущённого потока . Пусть x = 0, x = d > 0  есть абсциссы соответственно точек задней кромки B и передней кромки D профиля L_z, и для абсцисс всех остальных точек L_z имеет место соотношение 0 < x < d.

Будем считать, что всюду  на L_z функция тока ψ = 0, точка разветвления A потока находится на нижней поверхности L_z и потенциал скорости в ней φ = φ_A = 0.. Примем, что B есть точка схода потока. Примем, что  потенциал скорости на L_z есть непрерывная функция точек L_z, исключая точку B. Значения потенциала скорости φ в точке B при подходе к ней по точкам верхней и нижней поверхности L_z обозначим соответственно φ = φ_B и φ = φ_H, φ_B > φ_H > 0. Пусть D_z – область, внешняя для контура L_z.

Функция w = w(z) отображает конформно область D_z с разрезом по линии, лежащей вне контура L_z и соединяющей точки B, z = ∞, на область D_w в плоскости w = φ + iψ, разрезанной по положительной части действительной оси с началом в точке A, отвечающей w = 0, когда дуге AB нижней поверхности L_z соответствует отрезок верхнего берега вышеуказанного разреза, для точек которого выполняется соотношение 0 < φ < φ_H, а дуге ADB контура L_z – отрезок нижнего берега указанного разреза, для точек которого имеет место соотношение 0 < φ < φ_B.

Обозначим где v – модуль скорости, η – угол наклона к действительной оси вектора скорости в точке z = x + iy потока жидкости.

Как показано в ([1], с. 97-105), если контур L_z неизвестен, на нем задано распределение скорости v = v(s),  где s – дуговая абсцисса точки x + iy профиля L_z, отсчитываемая от точки A в направлении, при котором область D_z остается справа, l – периметр контура L_z, и требуется найти его форму, то эта задача оказывается разрешимой лишь при выполнении условий разрешимости – условия замкнутости контура L_z. Методы преодоления возникших при этом трудностей и подробный обзор работ по указанной проблеме изложены в книге [2].

В связи со сказанным представляется целесообразным рассмотрение задач об определении формы профиля L_z, которые оказываются разрешимыми.

В качестве такой задачи рассмотрим следующие: требуется найти форму профиля L_z, если на участке где  точки соответственно верхней и нижней поверхности L_z, потенциал скорости φ задан как функция абсциссы x точки L_z, а на участке  как функция одинаты y точки  z в виде

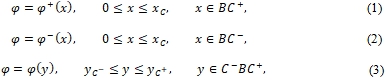
 где  заданные числа, 0 < x_A < x_C < d, x_C – абсцисса точек  ординаты точек  соответственно,  x_A – заданная абсцисса точки A,  величина d определяется в процессе решения, причем  заданные числа, циркуляция скорости вдоль L_z.

Будем считать, что  дифференцируемые функции, производные которых удовлетворяют условию Гёльдера в интервалах их задания, включая концы, причем  исключая точку A, 

Примем, что в окрестности точки x = x_A справедливо представление  где Ф - функция, удовлетворяющая условию Гёльдера в указанной окрестности точки 

Кроме того, будем считать заданной величину скорости  набегающего потока, которая является важной характеристикой указанного потока.

В соответствии с условиями (1)-(3) на L_z являются заданными точки  выбор которых влияет на форму L_z.

Поставленная выше задача отличается от рассмотренной в статье [3] только тем, что в последней величина  не задается и решение задачи зависит от одной действительной производной постоянной. Следовательно, решение рассматриваемой здесь задачи можно получить из решения, данного в [3], при соответствующем подборе входящей в решение постоянной.

При этом получаемое здесь решение будет зависеть от  и иметь свои отличительные особенности. В частности, в отдельных случаях решений может быть два или решения может не быть вовсе.

Вначале приведем используемые в дальнейшем формулы, полученные в работе [3].

В плоскости комплексного переменного  берется окружность  обтекаемая циркуляцией Г потоком с комплексным потенциалом

   (4)

где  действительные постоянные, которые выбираются так, чтобы функция (4) отображала область  на область D_w в плоскости w, когда точки  в которых  являются соответственно точками разветвления и схода потока,  находится из уравнения  вышеуказанные числа.

В формуле (4) под  понимается однозначная непрерывная ветвь в области  разрезанной по линии с уравнением  с началом в точке .

Соотношения w = w(z), w = ω(ς) определяют функцию z = z(ς), отображающую конформно область   на область D_z. Она имеет простой полюс ς =∞. Граничные значения этой функции равны  и  определяют соответствие точек L_z и окружности  при указанном отображении. Пусть точкам  окружности  при этом отвечают точки L_z  соответственно  Для определенности принимается, что

С учетом (4) из равенства   имеем

здесь 

Из первых равенств (5) находится зависимость  причем  из последнего равенства (5) определяется зависимость 

Таким образом, для искомой функции z(ς) получаются краевые условия

Для аналитической функции  с простым полюсом ς =∞ и краевыми значениями справедливо краевое условие

где

В формуле  под  понимается непрерывная в области  ветвь с граничными значениями  на остальных участках интервала (0, 2π).

Условие (6) представляется так:

где 

Таким образом, приходим к задаче Шварца для аналитической в области  функции  с простым полюсом . Пользуясь известным решением этой задачи ([4, С. 269-271, 287]), получаем формулу

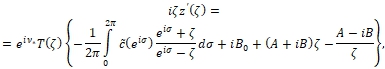   (7)

где произвольные действительные постоянные.

Функция  производная которой определяется формулой (7) должна быть однозначной, следовательно, вычет функции  формулы (7) в точке ς =∞ должен быть равным нулю:

где  Отсюда получим    (8) где 

Следовательно  должны быть функциями от  определяемыми формулами (8). В дальнейшем будем считать в формуле (7)

В соотношении (7) перейдем к пределу при   тогда, обозначая  будем иметь ([4, С. 39, 59])

   (9)

    (10)

Зная производную  формулы (9), найдем функцию  в интервале  аналогично по значениям  определим функцию  в интервалах . Следовательно, определим координаты  точек контура L_z. Форма этого контура зависит от произвольной действительной постоянной 

Обозначая  при  на основании равенства  приходим к формуле

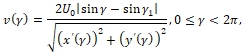     (11)

для вычисления распределения скорости  на L_z, зависящей от  в силу (9), (10).

Так как  и согласно (7)  то  отсюда получаем выражение

Из формулы для v_∞ приходим  к соотношению которые с учетом (10) запишем в виде . Это соотношение служит для определения значения постоянной , так как согласно постановке задачи величина v_∞ считается заданной. Ясно, что здесь должно выполняться условие  (при невыполнении этого условия поставленная задача неразрешима). Тогда постоянная  в частности определяется формулой . (Единственным будет значение ). Подставляя полученное в формулу (10), найдем  – значения постоянных, входящих в формулы (7), (9), (10), (11) и определим искомые функции . Если взять  то получим другое решение задачи.

Используя результаты статьи [5] легко убедиться в том, что определяемая с учетом формул (9), (10) производная   непрерывна в точке . Как видно из формул (9), (10), эта производная в точке  обращается в бесконечность, точка  контура L_z является угловой, и скорость v в ней равна нулю.

Область D_z должна быть однолистной, так как в противном случае задача обтекания профиля L_z станет физически нереализуемой. Проблема однолистности области D_z в изучаемой обратной краевой задаче требует особого рассмотрения.

Уместно отметить лишь следующее. Нетрудно убедиться в том, что если сумма в квадратных скобках формул (9), (10) в точке  принимает отрицательное значение, то область D_z будет неоднолистной. Поэтому постоянная  указанных формул должна удовлетворять неравенству:  которое с учетом (10) можно записать так:  Для выполнения этого неравенства выбранное выше значение  является предпочтительным чем положительное. Ясно, что это неравенство связано с поведением линии L_z вблизи точки  и не является достаточным условием однолистности области D_z.

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Тумашев Г.Г. Обратные краевые задачи и их приложения / Г.Г. Тумашев, М.Т. Нужин. – Казань: Изд-во КГУ. 1965. – 333 с.
2. Елизаров А.М. Обратные краевые задачи аэрогидродинамики / А.М. Елизаров, Н.Б. Ильинский, А.В. Поташов. –М.: Наука. 1994. – 440 с.
3. Салимов Р.Б. Решение обратной краевой задачи аэрогидродинамики в новой постановке / Р.Б. Салимов // Известия вузов. Математика. 2017, №9 – С. 96-101.
4. Гахов Ф.Д. Краевые задачи / Ф.Д. Гахов. – М.: Наука, 1977. – 641 с.
5. Салимов Р.Б. К вычислению сингулярных интергалов с ядром Гильберта / Р.Б. Салимов // Известия вузов. Математика. 1970, №12 – С. 93-96.

Список литературы на английском языке / References in English

1. Tumashev G.G. Obratnyi kraevie zadachi I ih prilozenia [Inverse boundary value problems and their applications] / G.G. Tumashev, M.T. Nuzhin. – Kazan: KSU publishing house. 1965. – 333 p. [in Russian]
2. Elizarov A.M. Obratnyi kraevie zadachi aerogidrodinamyki [Reverse regional tasks of aerodynamics] / A.M. Elizarov, N.B. Ilyinsky, A.V. Potashov. – M.: Science. 1994. – 440 p. [in Russian]
3. Salimov R.B. Rashenye obratnoy kraevoy zadachi aerogidrodinamyki v novoy postanovke [Solving the reverse edge of the aerodynamics in the new production] / R.B. Salimov // Bulletin of universities. Mathematics. – 2017 – No.9 – P. 96-101. [in Russian]
4. Gahov F.D. Kraevye zadachi. [Boundary value problems] M.:Nauka, 1977. – 641 p. [in Russian]
5. Salimov R.B. K vychisleniu singulyrnikh integralov s yadrom Hilberta [To the calculation of singular intergals with the core of Hilbert] / R.B. Salimov // Bulletin of universities. Mathematics. – 1970, – No.12 – P. 93-96. [in Russian]