ОСОБЕННОСТИ ПОВЕДЕНИЯ ОДИНОЧНЫХ КАПЕЛЬ В ЖИДКИХ ЭКСТРАКЦИОННЫХ СИСТЕМАХ

Русинова З.Р.

Старший преподаватель, Уральский федеральный университет имени первого Президента России Б.Н. Ельцина

ОСОБЕННОСТИ ПОВЕДЕНИЯ ОДИНОЧНЫХ КАПЕЛЬ В ЖИДКИХ ЭКСТРАКЦИОННЫХ СИСТЕМАХ

Аннотация

Знание скоростей движения капель имеет большое значение при расчете многих процессов химической технологии, в частности, процессов жидкостной экстракции. В промышленных аппаратах экстракционная система представляет собой сложную полидисперсную многофазную систему, для изучения которой первым шагом служит рассмотрение процессов, связанных с одиночной каплей. В данной работе экспериментально изучены особенности поведения одиночных всплывающих капель в системах бензол-вода и бутилацетат-вода. Особое внимание уделялось обеспечению высокой степени чистоты изучаемых систем. Показаны характерные режимы движения капель в зависимости их размера. Приведено сравнение полученных экспериментальных данных с некоторыми корреляциями, доступными в литературе.

Ключевые слова: жидкостная экстракция, скорость всплытия капли, коэффициент сопротивления, осцилляции, деформации, межфазная поверхность.

Rusinova Z.R.

Senior teacher, Ural Federal University named after the first President of Russia B.N.Yeltsin

BEHAVIOR OF SINGLE DROPLETS IN LIQUID EXTRACTION SYSTEMS

Abstract

The knowledge of drop rates has a big impotence to compute different processes of chemical technology, in particular, extraction processes. In industry extraction system is the complex polidisperse system. The first step to know these systems is to consider the behavior of a single drop. An experimental study of drop rise velocities was carried out in the system butyl acetate / water and benzene / water. A large effort has been made to prevent the system from contaminations. Typical regimes of droplet movement were shown in dependence of drop sizes. Correlations from the literature show excellent agreement with experiments.

Keywords: liquid extraction, drop rise velocity, drag coefficient, oscillations, deformations, interfacial surface.

В химической промышленности широко распространены процессы, протекающие в жидких дисперсных системах. В частности, к таким процессам относится жидкостная экстракция, которую проводят в распылительных колоннах, тарельчатых скубберах, роторно-дисковых экстракторах. Во всех этих аппаратах процесс массопереноса протекает на сферической границе раздела фаз. При этом коэффициент массопереноса непосредственно зависит от размера капель и скоростей их движения. Первым этапом для понимания процессов, протекающих в сложных многофазных полидисперсных системах в промышленных колоннах, является рассмотрение гидродинамического поведения одиночной капли.

Поведение одиночной капли имеет сложную природу и зависит от большого количества факторов. Прежде всего, стоит отметить, что движение пузырьков и жидких капель отличается от движения твердых сфер. Касательная составляющая скорости на границе раздела фаз отлична от нуля, из-за чего внутри капли возникают циркуляционные потоки и за счет чего скорость капли выше скорости твердой сферы [1,2]. Также, поскольку межфазная граница является подвижной, капли могут деформироваться и колебаться. Деформация и колебание капель определяются значениями критериев Рейнольдса и Вебера [1,3,4].

Известно, что наличие загрязнений в системе изменяет структуру потоков вокруг пузырьков и капель, замедляя межфазное движение. Широкое распространение получила модель, описывающая потоки жидкости вблизи поверхности капли [5-8]. Она предполагает, что поверхностно-активные загрязнения накапливаются на поверхности за движущейся каплей, образуя неподвижную «шапку» на поверхности, в то время как остальная поверхность капли остается подвижной. В [9] отмечается, что даже следовые количества поверхностно-активных загрязнений имеют сильное влияние на движение капель и массоперенос между дисперсной и сплошной фазой.

В течение нескольких последних десятилетий многие группы исследователей занимались вопросом свободного движения капли в неподвижной среде. Разработаны корреляции, описывающие предельные скорости движения капель, однако большинство из них подходят для расчета только загрязненных систем [10-12]. В последние годы стали широко применятся расчетные модели на основе методов вычислительной гидродинамики, которые позволяют моделировать многопоточные системы с различной геометрией [13-16].

В данной работе ставилась цель получить экспериментальные данные по скоростям движения в воде всплывающих органических капель и сравнить их с существующими корреляциями для расчета предельных скоростей движения капель. При этом особое внимание уделялась обеспечению высокой степени чистоты экспериментальной системы.

Схема установки изображена на рисунке 1. Исследования по измерению скоростей движения капель проводились в колонне 1 из боросиликатного стекла с внутренним диаметром 75 мм и высотой 1000 мм. Колонна оборудована теплообменной рубашкой 2, в которую заливается глицерин. Температура глицерина поддерживается на уровне 25 ºС при помощи термостата 7. Дисперсная фаза подается шприцевым насосом 4. Для того, чтобы создавать капли нужного размера, используется электромагнитное устройство 5, связанное с капилляром 9, на конце которого образуются капли. Электромагнитное устройство генерирует быстрые импульсы через заданные промежутки времени, за счет которых игла резко опускается вниз и отделяются капли нужного размера. Для создания капель большого диаметра использовались стальные капилляры размером 3х0,5 мм, для капель среднего размера – 1,1х0,25 мм и для мелких капель – 0,3х0,1 мм. Перед проведением опытов дисперсную и сплошную фазу взаимонасыщали, чтобы исключить массообмен между растворителями в ходе эксперимента.

Для определения мгновенных скоростей капель проводилась видеосъемка их движения с использованием высокоскоростной видеокамеры 3. В исследовании использовались следующие настройки камеры: пространственное разрешение 640х480 пикселей и частота 50 кадров в секунду. Для того чтобы обеспечить достаточную освещенность, использовались люминесцентные лампы мощностью 18 Вт.  Отснятые последовательности кадров переносились на ПК для последующего определения скоростей всплытия капель.

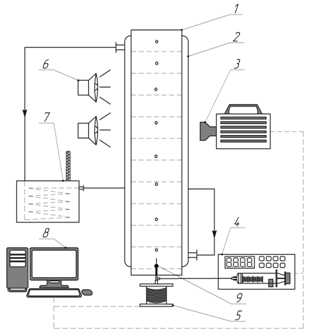
Рис. 1 – Схема экспериментальной установки: 1 - колонна, 2 – рубашка, 3 – видеокамера, 4 – шприцевой насос, 5 – электромагнитное устройство, 6 – люминесцентные лампы, 7 – термостат, 8 – ПК, 9 – капилляр

Как уже было отмечено выше, система является высокочувствительной к загрязнениям. По этой причине в установке использовались только 3 типа материалов: нержавеющая сталь, стекло и фторопласт-4. Кроме того особые требования предъявлялись к чистоте растворителей, поэтому в исследовании применялись химические вещества с квалификацией «осч» и бидистилированная вода. Физические свойства веществ перечислены в таблице 1.

Таблица 1 – Физические свойства веществ при 25 ºС

Вещество	Плостность, кг/м3	Вязкость, мПа·с	Межфазное натяжение на границе с водой, мН/м
Бензол	874	0,604	34,4
Бутилацетат	880	0,685	14
Вода	998	0,907	-

 

Максимальная и средняя характерная скорости движения капли определяются по схеме, представленной на рисунке 2. Максимальная скорость v_макс определяется при вычислении средней максимальной скорости, полученной в 10 измерениях. Средняя характерная скорость v_ср рассчитывается, как расстояние, пройденное каплей от момента окончания максимальной осцилляции до момента достижения конца колонны, разделенное на время прохождения этого расстояния Δt.

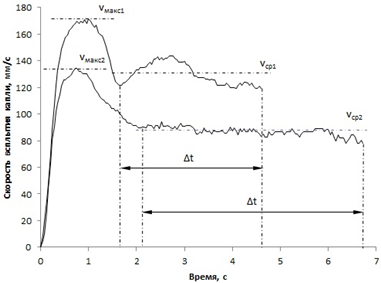
Рис. 2 – Схема определения максимальной и средней скорости движения капли

В эксперименте генерировались капли бутилацетата диаметром от 1 до 5 мм и капли бензола диаметром от 1,5 до 7 мм. В этом диапазоне размеров в зависимости от поведения капель при их всплытии можно условно выделить 3 режима движения капель:

1. Сферический режим – форма капли на протяжении всего времени её всплытия практически не отклоняется от сферической; мгновенная скорости капли в момент отрыва от капилляра увеличивается от нуля до максимального значения, которое затем не изменяется;
2. Переходный режим – при увеличении диаметра форма всплывающей капли все сильнее деформируются, и капля приобретает сплюснутую форму; при некотором диаметре предельная скорость всплытия капли начинает снижаться;
3. Колебательный режим – происходят колебания формы капли по направлению всплытия; с увеличением диаметра предельная скорость капли несколько снижается.

На рисунке 3 показано, как меняется форма капли во время всплытия в случае, когда капели движутся в переходном режиме (рис.3, а) и в колебательном режиме (рис. 3, б). Видно, что капля, движущаяся в переходном режиме, сохраняет сплюснутую форму в течение всего времени всплытия.

Рис. 3 – Фотографии капель бензола, движущихся в переходном (а) и колебательном (б) режимах

На рисунке 4 показано сравнение полученных экспериментальных данных с некоторыми существующими корреляциями, которые используются для расчета предельных скоростей движения капель.

Движение капель, которые при всплытии сохраняют сферическую форму, применяется модель, полученной Гамеликом и др.[17]:

где C_D – коэффициент сопротивления, μ* - отношение вязкости дисперсной фазы к вязкости сплошной фазы, Re – критерий Рейнольдса.

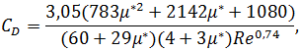
В случае с более крупными каплями деформации значительно влияют на коэффициент сопротивления, и скорость всплытия снижается до более низкого значения. В работе [18] Торсеном и др. предлагается следующая зависимость для расчета скоростей движения осциллирующих капель:

где σ  – межфазное натяжение системы растворителей, Н/м, ρ_p  - плотность дисперстной фазы, кг/м³, ρ_s - плотность сплошной фазы, кг/м³, d – диаметр капли, м.  

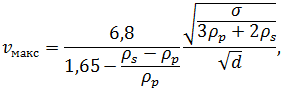
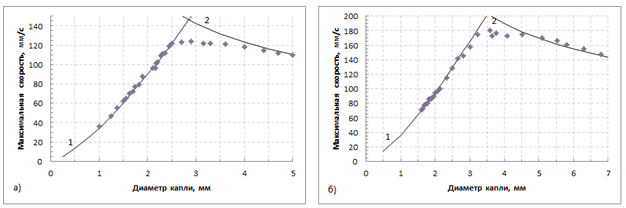
Рис.4 – Зависимость максимальной скорости всплытия капель бутилацетата (а) и бензола (б)  от диаметра капель. Экспериментальные данные и численные расчеты: (1) – Гамелик и др. [17], (2) – Торсен и др. [18]

Из рисунка 4 видно, что предельные скорости капель бензола и бутилацетата, движущихся в сферическом режиме, хорошо описываются с применением корреляции, полученной в работе [17]. Несмотря на то, что в [17] указано, что модель применяется при значениях критерия Рейнольдса не выше 100, в данных экспериментальных системах она хорошо описывает скорости при более высоких значениях критерия. Скорости капель бензола и бутилацетата, движущихся в осциллирующем режиме (начало деформаций наблюдается при значении числа Вебера We=4) также с высокой точностью описываются с помощью корреляции, полученной в работе [18].

Начало осцилляций наблюдалось для капель диаметром 4,5 мм в системе бензол/вода и для капель диаметром 3,9 мм в системе бутилацетат/вода.

Список литературы / References

1. Deen W. M. Analysis of Transport Phenomena / W. M. Deen. – New York: Oxford University Press, 1998.
2. Calderbank P. H. Circulation in liquid drops / P. H. Calderbank, I. J. O. Korchinski // Chemical Engineering Science. – 1956. – Vol. 6 (2). – P. 65–78.
3. Krishna P. M. Fall of liquid drops in water, Terminal Velocities / P. M. Krishna, D. Venkateswarlu, G. S. R. Narasimhamurty // Journal of Chemical Engineering . – 1959. – Vol. 4 (4). – P. 336–340.
4. Winnikow S. Droplet motion in purified systems / S. Winnikow, B. T. Chao // Phys. Fluids. – 1966. – Vol. 9 (1). – P. 50–61.
5. Griffith R. M. The effect of surfactants on the terminal velocity of drops and bubbles / R. M. Griffith // Chemical Engineering Science. – 1962. – Vol. 17. – P. 1057–1070.
6. Edge R. M. The motion of drops in water contaminated with a surface-active agent / R. M. Edge, C. D. Grant // Chemical Engineering Science. – 1972. – Vol. 27. – P. 1709–1721.
7. Levan D. The effect of surfactant on the terminal and interfacial velocities of a bubble or drop / D. Levan, J. Newman // AIChE Journal. –1976. – Vol. 22. – P. 695–701.
8. Hatanaka, J. Terminal velocity of a contaminated drop at low Reynolds numbers / J. Hatanaka , K. Maruta , S. Asai // The Chemical Engineering Journal. – 1988. – Vol. 39. – P. 185–189.
9. Li X. J. Effects of surface-active agents on mass of a solute into single buoyancy driven drops in solvent extraction systems / X. J. Li , Z. S. Mao, W. Y. Fei // Chemical Engineering Science. – 2003. – Vol. 58 (16). – P. 3793–3806.
10. Hu S. The fall of single liquid drops through water / S. Hu, R. C. Kintner // AIChE Journal. – 1955. – Vol. 1 (1) . – P. 42–48.
11. Klee A.J. Rate of rise or fall of liquid drops / A. J. Klee, R. E. Treybal //  AIChE Journal. – 1956. – Vol. 2 (4). – P. 444–447.
12. Clift R. Bubbles, Drops and Particles / R. Clift, J. R. Grace, M. E. Weber. – New York: Academic Press, 1978.
13. Eiswirth R. T. Experimental and numerical investigation of a free rising droplet / R. T. Eiswirth, H. J. Bart, T. Atmakidis, E. Y. Kenig // Chem. Eng. Process.: Process Intensif. – 2011. – Vol. 50 (7). – P. 718–727.
14. Wegener M. Transient rise velocity and mass transfer of a single drop with interfacial instabilities – numerical investigations / M. Wegener, T. Eppinger, K. Bäumler, M. Kraume, A. R. Paschedag, E. Bänsch // Chemical Engineering Science. – 2009. – Vol. 64. – P. 4835–4845.
15. Baumler K. Drop risevelocities and fluid dynamic behavior in standard test systems for liquid/liquid extraction—experimental and numerical investigations / K. Baumler, M. Wegener, A. R. Paschedag, E. Bansch // Chemical Engineering Science. – 2011. – Vol. 66. – P. 426–439.
16. Bertakis E. Validated simulation of droplet sedimentation with finite-element and level-set methods / E. Bertakis, S. Groß , J. Grande, O. Fortmeier, A. Reusken, A. Pfennig / Chemical Engineering Science . – 2010. – Vol. 65 (6). – P. 2037–2051.
17. Hamielec A.E. Viscous flow around fluid spheres at intermediate Reynolds –numbers / A. E. Hamielec, S. H. Storey, J. M. Whitehead // Journal of Chemical Engineering. – 1963. – Vol. 12. – P. 246–251.
18. Thorsen G. On the terminal velocity of circulating and oscillating liquid drops / G. Thorsen, R. M. Stordalen, S. G. Terjesen // Chemical Engineering Science. – 1968. – Vol. 23(5). – P. 413–426.