ПРОГРАММА ДЛЯ РАСЧЕТА ПАРАМЕТРОВ «ПУЗЫРЬКА» ПОЗИТРОНИЯ

Пивцаев А.А.¹, Разов В.И.²

¹ ORCID: 0000-0002-5514-9422, аспирант, ² Кандидат физико-математических наук, доцент, Дальневосточный федеральный университет

ПРОГРАММА ДЛЯ РАСЧЕТА ПАРАМЕТРОВ «ПУЗЫРЬКА» ПОЗИТРОНИЯ

Аннотация

В настоящее время существует много моделей, описывающих поведение позитрона и позитрония в жидкостях и растворах. Но, в своём большинстве, эти модели, не учитывают то, что параметры «пузырька» зависят от характеристик растворов. А значит получающиеся результаты не могут быть полностью достоверны истинным показателям. Наша программа, написанная по модели, описанной в статье Бучихина [1], учитывает все характеристики растворов и жидкостей, влияющих на изменение параметров «пузырька» и позволяет быстро, и легко рассчитать эти параметры.

Ключевые слова: позитроний, позитронная аннигиляционная спектроскопия с временным разрешением, «пузырьковая» модель.

 

Pivtsaev A.A.¹, Razov V.I.²

¹ ORCID: 0000-0002-5514-9422, Postgraduate student, ² PhD in Physics and mathematics, associate professor, Far Eastern Federal University

THE PROGRAM FOR CALCULATION OF PARAMETERS OF POSITRONIUM "BUBBLE"

Abstract

Currently, there are many models that describe the behavior of the positron and positronium in liquids and solutions. But for the most part, these models do not take into account that the parameters of the "bubble" depend on the characteristics of the solutions. So the results obtained may not be completely reliable indicators of true. Our program was written by the model described in the article Buchihina [1], takes into account all the characteristics of solutions and liquids that affect the change of parameters "bubble" and allows you to quickly and easily calculate these parameters.

Keywords: positronium, positron annihilation spectroscopy with a time resolution, "bubble" model.

 

Пузырьковая модель была введена Ferrell [2], чтобы оценить увеличение времени жизни pick–off  распада ортопозитрония  в жидкостях. Этот процесс, посредством которого позитрон в ортопозитронии  чувствует электроны с противоположным спином в окрестности, называется двухфотонная аннигиляция. Уменьшение оценки (по сравнению с ожидаемой) было приписано отталкиванию молекул растворенным позитронием через отталкивающее взаимодействие, возникающее от электрона, распределяющееся (обменивающееся) между двумя (Ps и молекулами). Как и предполагалось, это будет вести к локализованному состоянию позитрония внутри пузырька или потенциальной ямы.

Величина pick-off аннигиляции λ_p от атомов (или молекул) в окружающей жидкости, согласно Роеллигу [3], дается формулой:

λ_p = π r₀²c Z_eff n P_out                                        (1)

где r₀ классический радиус электрона, c – скорость света, n – плотность молекул на участке аннигиляции в жидкости, и Z_eff  - эффективное число электронов входящих в молекулу при pick-off аннигиляции позитронов в o-Ps. Медленные позитроны не могут проникнуть глубоко в атом, вклад в Z_eff дают только валентные электроны. P_out – вероятность выхода атома позитрония за пределы потенциальной ямы:

P_out =                                                 (2)

где R – радиус «пузырька» позитрония, k – коэффициент пропорциональсности.

Соотношения (1), (2) и граничные условий дают возможность, по измеренным характеристикам аннигиляционнных спектров [4], рассчитать величины kR, R, U.

Нами была написана программа для расчета размера (R) «пузырька». С помощью которой были сверены результаты, полученные в другой статье [5]. Результаты представлены в таблице 1.

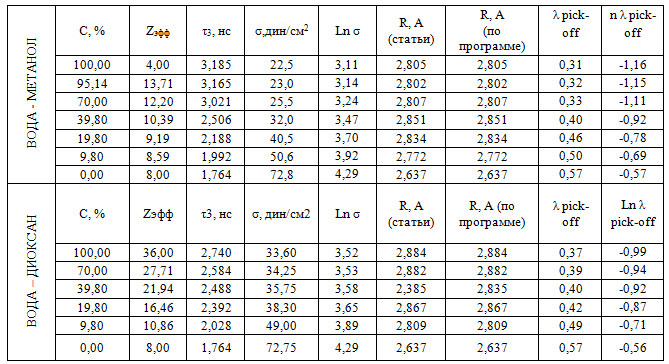
Таблица 1. Сравнение данных, полученных и взятых из статьи.

По данным таблицы видно, что радиус «пузырька» позитрония, рассчитанный по нашей программе с точностью до тысячных совпадает с данными статьи, а значит данные соответствуют формулам (1) и (2).

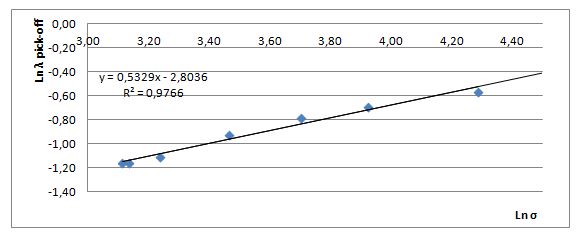
Для подтверждения достоверности полученных результатов был построен график зависимости Ln λ от Ln σ, рисунок 1. Ведь согласно формуле, приведенной в статье [6]:

 λ _pick-off = 0,07* σ^1/2                                              (3)

если прологарифмировать выражение (3), то графиком зависимости, должна быть – прямая.

Рисунок 1. График зависимость Ln λ от Ln σ.

На рисунке 1 видно, что  погрешность точек графика меньше 5%, т. о. данные, полученные по нашей программе «Bubblemod», соответствуют выше признанным формулам параметров «пузырька» и аннигиляционных характеристик позитрония.

Программы.

(Для расчета жидкостей)

PROGRAM BUBBLEMOD

      INTEGER*2 iasc, iscan

        REAL T2, Z, V, L2, UR, GT, U

        REAL C0,K0,K1

         COMMON/P/P

         EXTERNAL F

      CHARACTER*60 NAME

      C0=4.5071

      K0=0.0387

      K1=1.378

C

      WRITE(*,1)

  1     FORMAT(4X,'TIP OF SAMPLE : ',A60)

        READ(*,2) NAME

  2     FORMAT(A60)

      WRITE(*,*) 'INPUT LIFETIME T2 (nsek)'

      READ(*,*) T2

      WRITE(*,*) T2

      WRITE(*,*) 'INPUT EFFECTIVE CHARGE  Z '

      READ(*,*) Z

      WRITE(*,*) Z

      WRITE(*,*) 'INPUT MOLAR VOLUME V '

      READ(*,*) V

      WRITE(*,*) V

      WRITE(*,*) 'INPUT VOLUME OF SURFACE-TENSION GT '

      READ(*,*) GT

      WRITE(*,*) GT

C

        L2=1/T2

         P=(V*L2)/(C0*Z)

      WRITE(*,*) ' INPUT LIMITS OF ZERO A,B'

      READ(*,*) A,B

      WRITE(*,*) A,B

         TOL=1.E-5

         Z0=ZEROIN(A,B,F,TOL)

        UR=SQRT( ABS( ( Z0*( TAN( Z0 ) - Z0 ) * GT )/SIN( Z0 )**4 ) )

        U=K0*UR

        R=Z0*K1/SQRT(U)

      WRITE(*,*)

      WRITE(*,*) 'T2 = ',T2,' (nsek)'

      WRITE(*,*)

      WRITE(*,*) 'L2 = ',L2

      WRITE(*,*)

      WRITE(*,*) 'Z eff = ',Z

      WRITE(*,*)

      WRITE(*,*) 'V = ',V,' (sm3/mol)'

      WRITE(*,*)

      WRITE(*,*) 'GT = ',GT,' (dyn/sm)'

      WRITE(*,*)

      WRITE(*,*) 'P(kR) = ',P

      WRITE(*,*)

      WRITE(*,*) 'kR = ',Z0

      WRITE(*,*)

      WRITE(*,*) 'U = ',U,' (eV)'

      WRITE(*,*)

      WRITE(*,*) 'R = ',R,' (angstrem A)'

      WRITE(*,*)

        WRITE(*,1) NAME

      WRITE(*,*)

        WRITE(*,*) 'DO YOU WANT HARD COPY ?(Y = "Yes",N = "No")'

         CALL ONKEYW(iasc,iscan)

         IF((iasc.EQ.89).OR.(iasc.EQ.121)) THEN

            WRITE(10,1) NAME

            WRITE(10,*)

            WRITE(10,*) '      MOLAR VOLUME V =',V,'(sm3/mol)'

            WRITE(10,*)

            WRITE(10,*) '      Z eff =',Z

            WRITE(10,*)

            WRITE(10,*) '      SURFASE-TENSION =',GT,'(dyn/sm)'

            WRITE(10,*)

            WRITE(10,*) '      P(kR)=',P

            WRITE(10,*)

            WRITE(10,*) '      kR=',Z0

            WRITE(10,*)

            WRITE(10,*) '      POTENTIAL DEPTH U=',U,'(electronvolts)'

            WRITE(10,*)

            WRITE(10,*) '      BUBBLE RADIUS R =',R,'(angstrem A)'

      ENDIF

      STOP

      END

         FUNCTION F(T)

         COMMON/P/P

         F=SIN(T)**2/(1.-T*COTAN(T))-P

         RETURN

         END

(Для расчета растворов)

PROGRAM BUBBLEMOD

        REAL T2,ML,MS,RL,RS,ZL,ZS,CL,CS,VL,WL,WS,Z,V,XL,XS,L2,UR,GT,U

        REAL C0,K0,K1

         COMMON/P/P

         EXTERNAL F

      CHARACTER*60 NAME

         C0=4.5071

        K0=0.387

        K1=1.949

C

        WRITE(*,1)

  1     FORMAT(4X,'TIPE OF SAMPLE : ',A60)

        READ(*,2) NAME

  2     FORMAT(A60)

        WRITE(*,*) 'INPUT LIFETIME T2 (nsek)'

        READ(*,*)T2

        WRITE(*,*)T2

        WRITE(*,*) 'INPUT MOLAR MASS OF SOLVENT ML (g/mol)'

        READ(*,*)ML

        WRITE(*,*)ML

        WRITE(*,*) 'INPUT MOLAR MASS OF SOLUTE MS (g/mol)'

        READ(*,*)MS

        WRITE(*,*)MS

        WRITE(*,*) 'INPUT DENSITY OF SOLVENT RL (g/ml)=(g/sm3)'

        READ(*,*)RL

        WRITE(*,*)RL

        WRITE(*,*) 'INPUT DENSITY OF SOLUTE RS (g/sm3)'

        READ(*,*)RS

        WRITE(*,*)RS

        WRITE(*,*) 'INPUT VOLUME OF SOLVENT VL (ml)'

        READ(*,*)VL

        WRITE(*,*)VL

        WRITE(*,*) 'INPUT MASS OF SOLUTE WS (g)'

        READ(*,*)WS

        WRITE(*,*)WS

        WRITE(*,*) 'INPUT EFFECTIVE CHARGE OF SOLVENT ZL eff'

        READ(*,*)ZL

        WRITE(*,*)ZL

        WRITE(*,*) 'INPUT EFFECTIVE CHARGE OF SOLUTE ZS eff'

        READ(*,*)ZS

        WRITE(*,*)ZS

        WRITE(*,*) 'INPUT VOLUME OF SURFASE-TENSION GT (dyn/sm)'

        READ(*,*)GT

        WRITE(*,*)GT

C       ****** вычисление моляpного объема pаствоpа ******

        WL=RL*VL

        CL=WL/(WL+WS)

        CS=WS/(WL+WS)

        V=(ML/RL)*CL+(MS/RS)*CS

c       ****** вычисление эффективного заpяда pаствоpа ******

        XL=(WL/ML)/(WL/ML+WS/MS)

        XS=(WS/MS)/(WL/ML+WS/MS)

        Z=ZL*XL+ZS*XS

c       ****** pассчет веpоятности выхода из ямы ******

        L2=0.693/T2

        P=(V*L2)/(C0*Z)

c       ****** опpеделение kR ******

        WRITE(*,*) ' INPUT LIMITS OF ZERO A'

        READ(*,*)A

        WRITE(*,*)A

        WRITE(*,*) ' INPUT LIMITS OF ZERO B'

        READ(*,*)B

        WRITE(*,*)B

        TOL=1.E-5

        Z0=ZEROIN(A,B,F,TOL)

C       ****** pассчет глубины потенциальной ямы ******

        UR=SQRT(ABS((Z0*(TAN(Z0)-Z0)*GT)/SIN(Z0)**4))

        U=K0*UR

c       ****** опpеделение pадиуса ямы ******

        R=Z0*K1/SQRT(U)

c       ****** вывод pезультатов на экpан ******

        WRITE(*,*)  'T2=',T2,'(nsek)'

        WRITE(*,*)  'WL=',WL,'(gramm)'

        WRITE(*,*)  'WS=',WS,'(gramm)'

        WRITE(*,*)  'CL=',CL

        WRITE(*,*)  'CS=',CS

        WRITE(*,*)  'XL=',XL

        WRITE(*,*)  'XS=',XS

        WRITE(*,*)  'Z eff =',Z

        WRITE(*,*)  'V=',V,'(sm3/mol)'

        WRITE(*,*)  'GT=',GT,'(dyn/sm)'

        WRITE(*,*)  'P(kR)=',P

        WRITE(*,*)  'kR=',Z0

        WRITE(*,*)  'U=',U,'(eV)'

        WRITE(*,*)  'UR=',UR

        WRITE(*,*)  'R=',R,'(angstrem A)'

        WRITE(*,1)NAME

        WRITE(*,*)  'DO YOU WANT HARD COPY ?(Y="Yes",N="No")'

        CALL ONKEYW(iasc,iscan)

        IF((iasc.EQ.89).OR.(iasc.EQ.121)) THEN

            WRITE(10,1)NAME

            WRITE(10,*)'SOLVENT CONCN Cl     =',CL

            WRITE(10,*)'SOLUTE CONCN Cs      =',CS

            WRITE(10,*)'SOLVENT MOLAR PART   =',XL

            WRITE(10,*)'SOLUTE MOLAR PART    =',XS

            WRITE(10,*)'MOLAR VOLUME V       =',V,'(sm3/mol)'

            WRITE(10,*)'Z eff                =',Z

            WRITE(10,*)'SURFASE-TENSION      =',GT,'(dyn/sm)'

            WRITE(10,*)'P(kR)                =',P

            WRITE(10,*)'kR                   =',Z0

            WRITE(10,*)'POTENTIAL DEPTH U    =',U,'(eV)'

            WRITE(10,*)'BUBBLE RADIUS R      =',R,'(angstrem A)'

        ENDIF

        STOP

        END

        FUNCTION F(T)

        COMMON/P/P

        F=SIN(T)**2/(1.-T*COTAN(T))-P

        RETURN

        END

Литература

1. Бучихин А. П., Гольданский В. И., Татур А. О., Шантарович В. И.. Атом Позитрония в органических жидкостях // Журнал экспериментальной и теоретической физики, Т. 60, вып. 3 – 1971, с.1136 – 1140.
2. Ferrell R. A. Phys. Rev., 1957, с. 108, с. 167.
3. Roellig L. O., Stewart A. T.. Proc. of the Conf. Held at Wayne State Univ. 1965, p. 127.
4. Пивцаев А. А., Разов В. И.. Исследование химических канцерогенов методом позитронной аннигиляционной спектроскопии с временным разрешением // Журнал прикладной спектроскопии, Т. 80, № 5, 2013, с. 806 – 809.
5. Бучихин А.П., Гольданский В.И., Татур А.О., Шантарович В.П. Атом позитрония в органических жидкостях.//Журнал экспериментальной и теоретической физики, - 1971. – 60, №3. – С. 1136 – 1140.
6. Tao SJ (1972) Positronium annihilation in molecular substances. J Chem Phys 56:5499–5510.

References

1. Buchihin A. P., Gol'danskij V. I., Tatur A. O., Shantarovich V. I.. Atom Pozitronija v organicheskih zhidkostjah // Zhurnal jeksperimental'noj i teoreticheskoj fiziki, T. 60, vyp. 3 – 1971, s.1136 – 1140.
2. Ferrell R. A. Phys. Rev., 1957, s. 108, s. 167.
3. Roellig L. O., Stewart A. T.. Proc. of the Conf. Held at Wayne State Univ. 1965, p. 127.
4. Pivcaev A. A., Razov V. I.. Issledovanie himicheskih kancerogenov metodom pozitronnoj annigiljacionnoj spektroskopii s vremennym razresheniem // Zhurnal prikladnoj spektroskopii, T. 80, № 5, 2013, s. 806 – 809.
5. Buchihin A.P., Gol'danskij V.I., Tatur A.O., Shantarovich V.P. Atom pozitronija v organicheskih zhidkostjah.//Zhurnal jeksperimental'noj i teoreticheskoj fiziki, - 1971. – 60, №3. – S. 1136 – 1140.
6. Tao SJ (1972) Positronium annihilation in molecular substances. J Chem Phys 56:5499–5510.