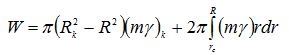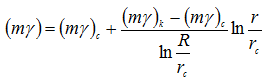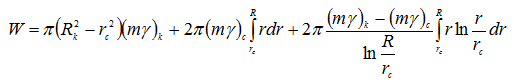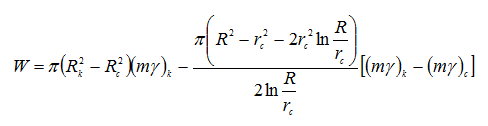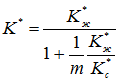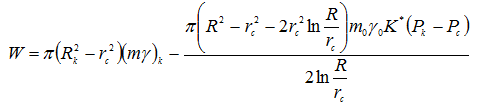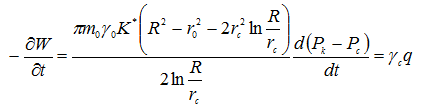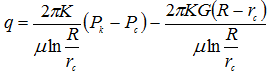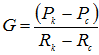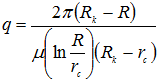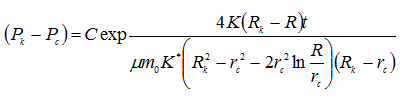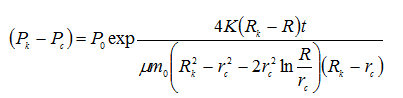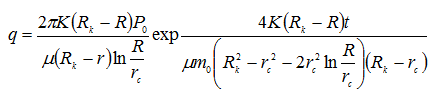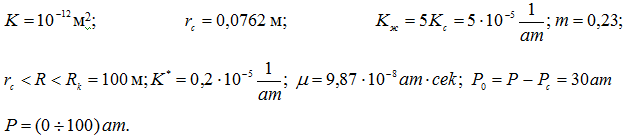ПЛOСКО-РАДИАЛЬНАЯ НЕСТАЦИОНАРНАЯ ФИЛЬТРАЦИЯ СЖИМАЕМОЙ ВЯЗКО-ПЛАСТИЕСКОЙ ЖИДКОСТИ В СЖИМАЕМОЙ ПОРИСТОЙ СРЕДЕ

Мустафаев С.Д.¹, Ибрагимов В.А.², Гулиев Р.А.³

¹ Кандидат технических наук, ² Кандидат физико-математических наук, Азербайджанский государственный университет нефти и промышленности, ³ Начальник Нефтегазодобывающего Управления им. А.Дж. Амирова

ПЛOСКО-РАДИАЛЬНАЯ НЕСТАЦИОНАРНАЯ ФИЛЬТРАЦИЯ СЖИМАЕМОЙ ВЯЗКО-ПЛАСТИЕСКОЙ ЖИДКОСТИ В СЖИМАЕМОЙ ПОРИСТОЙ СРЕДЕ

Аннотация

В статье применен метод последовательной смены стационарных состояний и решена аналитическая задача для плоско-радиального фильтрационного потока сжимаемой вязко-пластичной жидкости из сжимаемого кругового пласта к вертикальной скважине, расположенной в центре залежи, при этом получен алгоритм для дебита скважины, полученного из единицы толщины пласта в зависимости от текущего радиуса возмущения в дренажной зоне и времени эксплуатации скважин и на основе этого алгоритма по заданным исходным данным произведены численные подсчеты и построено семейство кривых, характеризующих ход процесса после мгновенного пуска скважины в режим работы.

Ключевые слова: сжимaемaя вязко-пластичная  жидкость, сжимаемая пористая среда, плоско-радиальный поток, нестационарная фильтрация, радиус депрессионного влияния.

Mustafayev S.D. ¹, Ibrahimov V.A. ², Guliyev R.A. ³

¹ PhD in Engineering, Аzerbaijan State Oil and Industry University, ² PhD in Physics and Mathematics, Аzerbaijan State Oil and Industry University, ³ Director of Oil and Gas Production Department

FLAT-RADIAI UNSTEADY FILTRATION OF INCOMPRESSIBLE VISCOUS-PLASTIC FLUID IN A COMPRESSIBLE POROUS MEDIUM

Аbstract

In the article the method of successive change of stationary states and solve analytical problem for plane-radial seepage compressible viscous-plastic fluid from a collapsible circular formation to a vertical well, located in the center of the deposit, with an algorithm for the well flow rate obtained from a unit of the thickness of the layer in Depending on the current radius of the disturbance in the drainage area and time of operation of wells and on the basis of this algorithm on the given input data and generated numerical counts a family of curves that characterize the course of the process, after starting well in the instant mode.

Keywords: compressible visco-plastic fluid compressible porous medium, flatradial flow, transient filtering, depression influence radius.

В работах [1,2] представлены решения задач о простых фильтрационных потоках сжимаемых ньютоновских жидкостей в сжимаемой пористой среде.

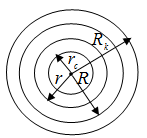
Рис.1. Схема кругового пласта

Пусть в центре круговой залежи, схематически представленной на рис.1, расположена эксплуатационная скважина. Допустим, что после ее пуска, за некоторое время t, радиус депрессионного влияния стал равен расстоянию R от скважины. Пользуясь методом последовательной смены стационарных состояний [1], определяется забойное давление скважины  соответствующее времени  после пуска скважины.

Отнеся расчет к единице мощности пласта, для веса жидкости в пласте имеем

(1)

Считая, что  в кольце  распределение стационарное, имеем

(2)

Подставляя (2) в (1), имеем:

(3)

Раскрыв интегралы и проведя алгебраические преобразования, имеем:

(4)

Выразим  (mγ) через давление

(5)

где 

 - коэффициент, учитывающий упругости пластовой жидкости и скелет породы;

γ - удельный вес пластовой жидкости;

γ₀ - удельный вес пластовой жидкости в начальный момент.

Тогда

(6)

где P_k - пластовое давление; P_c - забойное давление в скважине.

Дифференцируя (6) по t имеем

(6)

где q - дебит скважины из единицы толщины пласта; γ_с  - удельный вес пластовой жидкости на забое скважины.

Согласно [1]

(7)

где К - коэффициент проницаемости пласта; μ - коэффициент динамической вязкости пластовой жидкости.

Учитывая, что , из (7) имеем:

(8)

Приняв γ₀ = γ_с , из (7) и (9) получаем:

(9)

Откуда

(10)

Из практических соображений решение уравнения (9) должно удовлетворять условию:

(11)

Поэтому, учитывая (11) в (10), получаем:

(12)

Учитывая (12) в (9), получаем:

(13)

Рассмотрим численный пример.

Пусть для какой-то конкретной скважины и выкачиваемой нефтяной жидкости

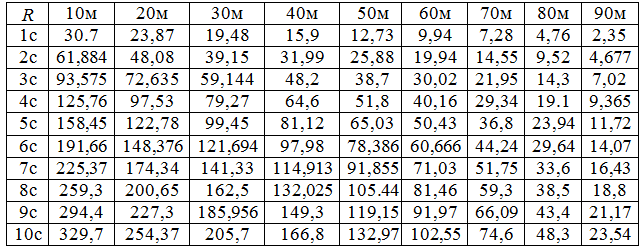
По этим данным по формуле (13) произведен расчет на ЭВМ. По результатам подсчета построена таблица (табл.1), на основании которой построены графики зависимости дебита от расстояния до скважины за количество суток (рис.2).

Таблица 1

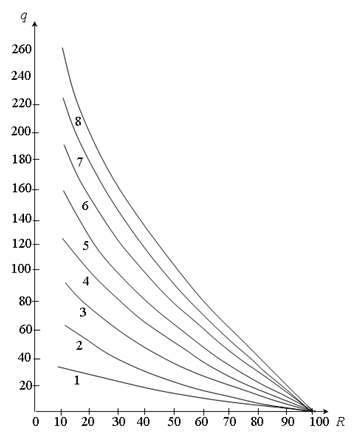
Рис.2. График зависимости дебита от (R) расстояния до скважины (в м³/сутки), где номера линий означают количество суток.

Анализируя результаты таблицы и построенных графиков, установлено:

1) С увеличением непрерывной продолжительности добычи, коли­чество выкачиваемой жидкости увеличивается по нелинейному закону, то есть количество выкаченной нефтяной массы за каждые сутки (хотя и не очень значительно) больше каждой из предыдущих суток.

2) По мере приближения к скважине дебит увеличивается по вогнутой кривой относительно оси R. Это означает, что в каждый момент времени непрерывного выкачивания нефти (в зависимости от ее вязкости) количество утекающей массы из любого радиального сечения пласта в сторону скважины больше количества протекающей.

Литература

1. Чарный И.А. Метод последовательной смены стационарных состояний и его приложения к залежам нестационарной фильтрации жидкостей и газов. Известия АН СССР, отделение техн. Наук, №3, 1949
2. Чарный И.А. Подземная гидрогазодинамика. Госкомтехиздат, Москва, 1963, с.272-284
3. Султанов Б.И. Исследование вопросов фильтрации в пористой среде нефтей и масел, обладающих структурно-механическими свойствами. Дисс. на соиск. уч. степени канд. Тех. наук, Баку, 1962, 153 с.

References

1. Charny I.A The method of successive change of stationary states and its application to the deposits of non-stationary filtration of liquids and gases. Proceedings of the Academy of Sciences of the USSR, Department tehn. Science, №3, 1949.
2. Charny I.A. Underground fluid dynamics. Goskomtehizdat, Moscow, 1963, s.272-284.
3. Sultanov B.I. Study on filtration in a porous medium oils and oils that have structural and mechanical properties. Diss, on soisk. Ouch. PhD degree. Those. Sciences, Baku, 1962, 153 p.