О ВЛИЯНИЕ ВНЕШНЕГО ШУМА НА СЦЕНАРИЙ РЮЭЛЯ-ТАКЕНСА-НЬЮХАУЗА В БАЛКАХ ТИМОШЕНКО

Крылова Е.Ю.¹, Душаканова Н. ², Папкова И.В. ³ (науч.рук.),  Бабенкова Т.В. ⁴

¹Кандидат физико-математических наук, Саратовский государственный университет им. Н.Г. Чернышевского, ² Студент,^{3, 4}Кандидат физико-математических наук, доцент Саратовский государственный технический университет им. Гагарина Ю.А.

О ВЛИЯНИЕ  ВНЕШНЕГО  ШУМА НА СЦЕНАРИЙ РЮЭЛЯ-ТАКЕНСА-НЬЮХАУЗА В БАЛКАХ ТИМОШЕНКО

Аннотация

Работа посвящена анализу влияния внешнего шума на параметрические колебания динамических систем. Показано, что с помощью внешнего воздействия можно управлять характером их колебаний.

Ключевые слова: нелинейная динамика, индуцированные шумом переходы,  параметрические колебания.

Krylova E.Y ¹, Dyshakanova N. ², Papkova I.V. ³, Babenkova T.B. ⁴

¹PhD in Physics and mathematics, Saratov State University, ²Student, ^3,4 PhD in Physics and mathematics, assosiate professor, Saratov State Technical University

ABOUT INFLUENCE OF EXTERNAL NOISE ON THE SCENARIO RUELLE-TAKENS-NEWHOUSE IN TIMOSHENKO BEAM

Abstract

The purpose of work is analysis of external noise influences on the  parametric oscillations of dynamical systems.

Keywords: nonlinear dynamics, noise-induced transitions, parametric oscillations.

В работе рассматривается влияние аддитивного внешнего шума на характер параметрических колебаний гибкой упругой  балки модели Тимошенко. В таких областях как физика, химия, биология, уже показано, что случайные воздействия играют весьма существенную роль в поведении динамических систем [1]. Внешние шумы способны приводить не только к флуктуациям в характеристиках динамических систем, но и вызывать качественную перестройку их режимов.

Рассматривается однослойная, упругая, изотропная балка, как область пространства  в декартовой системе координат XOZ (ось OX направлена слева направо вдоль срединной линии балки, ось OZ – вниз, перпендикулярно оси OX). Под срединной линией балки понимается фиксированная линия приведения z = 0. В указанной системе координат область, занимаемая балкой определяется в виде: , 2h – высота, а – длина балки.  Балка находится под действием поперечной знакопеременной нагрузки , приложенной к некоторой области балки, где  и  амплитуда и частота  нагрузки соответственно.

Математическая модель нелинейных диссипативных колебаний балки строится на основе гипотезы Тимошенко [2], с учетом нелинейной зависимости между деформациями и перемещениями в форме Кармана [3]. К уравнениям движения элемента балки присоединяются граничные условия шарнирного опирания  и нулевые начальные условия. Дифференциальная задача приводится к системе обыкновенных дифференциальных уравнений по пространственной координате методом конечных разностей (МКР) с погрешностью , которая по времени решается методом Рунге-Кутта четвертого порядка точности. Применение МКР позволяет рассматривать балку, как механическую систему с потенциально бесконечным числом степеней свободы.  Аддитивный шум добавлен в систему в форме случайного слагаемого с постоянной интенсивностью , где  - интенсивность шума. При исследовании колебаний результаты, полученные для центральной точки срединной линии балки, обобщаются на всю балку. При получении численных результатов использовались следующие параметры:  - отношение линейных размеров балки,  - коэффициент диссипации среды;  - число разбиений отрезка  в МКР;  - шаг по времени в методе Рунге-Кутты, .

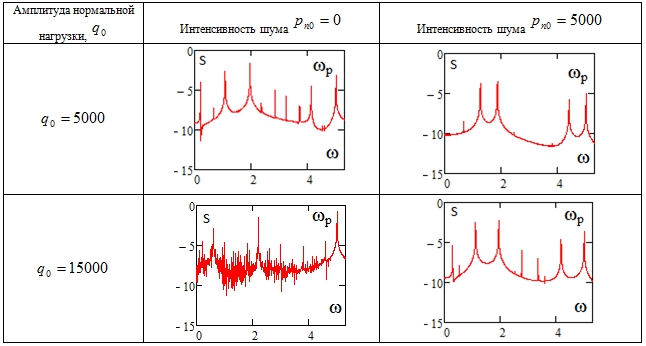
При частоте нормальной нагрузки  был получен сценарий Рюэля-Такенса-Ньюхауса. Далее проводился анализ влияния интенсивности аддитивного шума на характер колебаний балки.

Разрушения сценария Рюэля-Такенса-Ньюхауса  обнаружено не было.

В числебнных экспериментах с интенсивностью аддитивного шума менее  отмечалось, что при отношении амплитуды нормальной нагрузки к интенсивности шума более чем в 2 раз  происходит снижение реакции системы на шум. В случае , при превышении амплитудой внешней нагрузки  значение 50 спектр мощности Фурье стал очищаться в области частот больших . При  шумовая составляющая на спектре осталась только в области низких частот. При  спектр с учетом внешних флуктуаций и спектр без учета шумовой составляющей идентичны. В случае интенсивности шума  хаотическая реакция системы на внешний шум стала сокращаться при   шумовых составляющих в спектре Фурье почти не осталось.

В численных экспериментах с . Спектры мощность Фурье были серьезно зашумлены по всему рассматриваемому интервалу амплитуд внешней нагрузки (). Наблюдалось незначительное снижение реакции на аддитивный  внешний шум.

В численном эксперименте с интенсивностью внешнего шума   были обнаружены области, где система не только не проявляла хаотических реакций на внешнее шумовое воздействие, но и  под влиянием шумовой составляющей происходило уменьшение количества частот в спектре Фурье. Так, при  хаотические колебания под действием внешнего шума перешли в  квазипериодические (Таблица 1).

Полученные в результате численных экспериментов результаты  позволяют сделать вывод о том, что с помощью внешнего воздействия можно управлять характером колебаний  рассматриваемых распределенных механических систем.

 

Таблица 1

Литература

1. Хорстхемке В. Индуцированные шумом переходы: Теория и применение в физике, химии и биологии/ В. Хорстхемке, Р. Лефевр: Пер. с англ.-М.:Мир,1987.-400с.
2. Вольмир А.С. Нелинейная динамика пластинок и оболочек / А.С. Вольмир.- М.: Наука, 1972.- 492 с.
3. Karman, Th. Festigkeitsprobleme in Maschinenbau/ Th. Karman // Encykle. D. Math. Wiss. 1910. Vol. 4, №4, P. 311 – 385.

References

1. Horsthemke V. Inducirovannye shumom perehody: Teorija i primenenie v fizike, himii i biologii/ V. Horsthemke, R. Lefevr: Per. s angl.-M.:Mir,1987.-400s.
2. Vol'mir A.S. Nelinejnaja dinamika plastinok i obolochek / A.S. Vol'mir.- M.: Nauka, 1972.- 492 s.
3. Karman, Th. Festigkeitsprobleme in Maschinenbau/ Th. Karman // Encykle. D. Math. Wiss. 1910. Vol. 4, №4, P. 311 – 385.