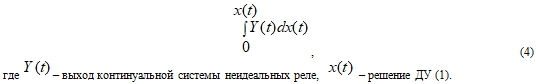НЕЛИНЕЙНЫЙ ОСЦИЛЛЯТОР С ГИСТЕРЕЗИСНЫМИ СВОЙСТВАМИ

Фомина Е.А.

Аспирант, Воронежский государственный университет

НЕЛИНЕЙНЫЙ ОСЦИЛЛЯТОР С ГИСТЕРЕЗИСНЫМИ СВОЙСТВАМИ

Аннотация

В статье рассмотрена математическая модель нелинейного осциллятора с гистерезисными свойствами. Получены качественные аспекты возникновения нерегулярных колебаний в нелинейной динамической системе.

Ключевые слова: нелинейный осциллятор, нелинейная динамическая система, диссипативность.

Fomina E.A.

Postgraduate student, Voronezh State University

NONLINEAR OSCILLATOR WITH HYSTERESIS PROPERTIES

Abstract

The article describes a mathematical model of a nonlinear oscillator with hysteresis properties. We got the qualitative aspects of irregular oscillations in nonlinear dynamical system.

Keywords: nonlinear oscillator, nonlinear dynamical system, dissipative.

Хаотические процессы в  детерминированных нелинейных системах - одна из фундаментальных проблем современного естествознания и основной объект внимания в нелинейной динамике. Область исследований здесь необычайно широка, поскольку охватывает анализ всех зависящих от времени явлений в различных системах, независимо от их природы. Так, например, в биологии и медицине большую роль играют физиологические ритмы, которые качественно меняются при переходе от нормы к патологии [1] или, например, предсказание погоды, которое также опирается на изучение турбулентности в атмосфере и попытке найти «порядок в хаосе».

Вопросам исследования возможных переходов от регулярных  к хаотическим режимам движения детерминированных динамических систем на фазовых плоскостях с периодическим возбуждением посвящена обширная библиография (см., например, [2]-[8]). Исследования отдельных областей фазового пространства систем, в которых имеют место устойчивые и неустойчивые колебания системы проведены в [2], [3],[6]-[8] с применением различных приближенных аналитических и численных методов, а также их сочетаний.

Простейшей нелинейной системой, в которой можно наблюдать вынужденные хаотические колебания, является осциллятор Дуффинга. Большое количество исследований было проведено на примере этой нелинейной системы и написано большое количество научных статей. Периодические вынужденные колебания, описанные  уравнением Дуффинга, предоставляют широкий спектр интересных явлений, которые характерны для поведения нелинейных динамических систем, такие как регулярное и хаотическое движение, сосуществующие аттракторы, регулярные и фрактальные границы областей притяжения, а также локальная и глобальная бифуркация.

Что касается нелинейных зависимостей гистерезисного типа, то они повсеместно возникают в различных разделах физики, механики, биологии и др. науках. Учет гистерезисных эффектов необходим во многих проблемах: гистерезис в задачах управления и биологии, ферромагнитный и диэлектрический гистерезис в физике, пластический гистерезис в механике и т.п. [9]-[16].

В хорошо известном нам уравнении Дуффинга нелинейным звеном выступает кубическая функция вида (1):

      (1)

В настоящей работе нелинейным элементом системы выбрано звено гистерезисного типа, с целью исследования поведения динамической системы с гистерезисными свойствами и анализа влияния управляющих параметров на развитие системы на длительных временах, а также последующими обобщением и систематизацией полученных результатов.

Нелинейный осциллятор с гистерезисными свойствами

Рассмотрим математическую модель нелинейного осциллятора  с гистерезисным звеном, на который оказывается периодическое воздействие.

Динамика системы описывается дифференциальным уравнением (2)  с начальными условиями (3):

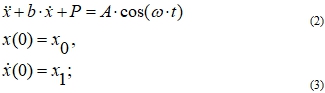
где  - конечная система неидеальных реле,  - набор неидеальных реле, на вход которых поступает ,  – решение рассматриваемой системы,  – пороговые числа, , A - амплитуда вынуждающей силы,  ω – частота, b – константа.

Как уже отмечалось ранее, целью данной работы является определение качественных аспектов возникновения (отсутствия) нерегулярных движений в рассматриваемой системе c гистерезисной нелинейностью, аппроксимируемой явным гистерезисным звеном -  конечной системой неидеальных реле; анализ поведения системы при изменении управляющих параметров: амплитуды вынуждающей силы, коэффициентов при гистерезисном звене, а также самой структуры гистерезисного звена; анализ влияния изменения начальных условий системы с целью определения устойчивости или неустойчивости нулевого решения системы (2)-(3), а также последующее обобщение и систематизация полученных результатов.

Оценка влияния изменений управляющих параметров на поведение системы

С помощью применения численных методов, и посредством построения   Simulink-схемы пакета Matlab было найдено численное решение системы (2)-(3). Управляющими параметрами системы являются: амплитуда внешнего возбуждения, структура гистерезисного звена (пороговые значения), коэффициенты при реле. В зависимости от значений данных параметров траектория движения системы имела вид: (см. рис.1.2 – 7.2).

Анализ поведения системы при изменении амплитуды вынуждающей силы

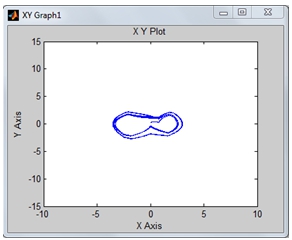
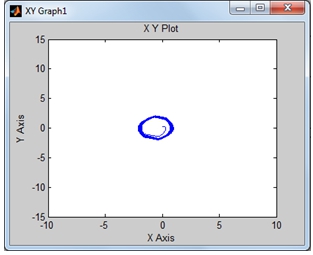
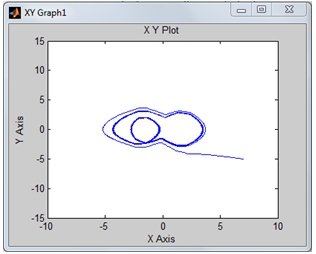
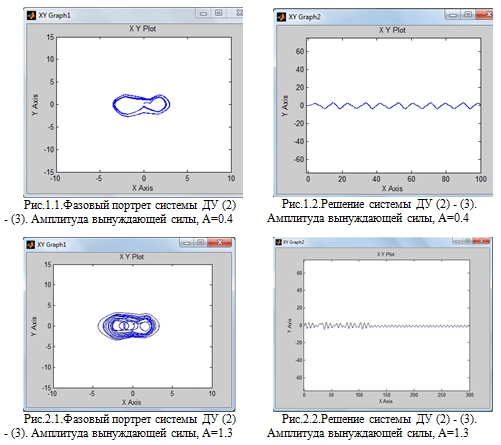
Первый этап исследований включал в себя тестирование поведения системы на наличие (отсутствие) нерегулярных колебаний при изменении амплитуды вынуждающей силы, A и получение соответствующих фазовых портретов системы. В результате многочисленных экспериментов, были получены промежутки на числовой оси, на которых система совершает нерегулярные колебания, а также промежутки – где поведение системы можно описать следующим образом, траектория системы находится в некоторой ограниченной области, т.е. система диссипативна (рис. 2.1, рис. 1.1.).

Рис.1.1 -Фазовый портрет системы ДУ (2) - (3). Амплитуда вынуждающей силы, А=0.4

Рис.2.1 - Фазовый портрет системы ДУ (2) - (3). Амплитуда вынуждающей силы, А=1.3

Чувствительная зависимость системы от начальных условий

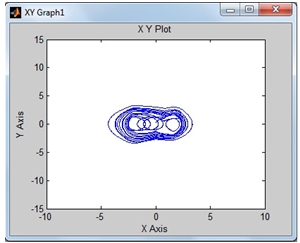
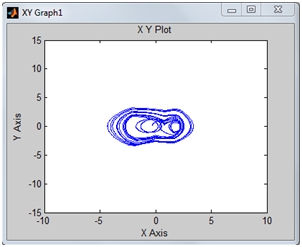
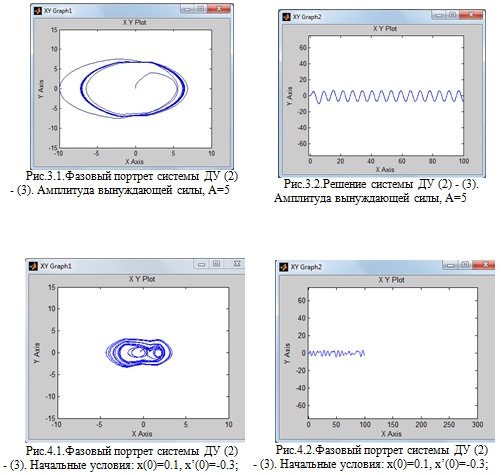
Вторым этапом в нашем исследовании было тестирование системы на ее зависимость к начальным условиям, так как, общеизвестно, что нелинейные динамические системы, в которых можно наблюдать хаотические колебания, чувствительно зависимы от начальных условий. По итогам численных экспериментов, мы получили, что наша система чувствительна к начальным условиям тогда, когда амплитуда вынуждающей силы достаточно велика. Причем, если начальные условия заданы в окрестности нуля, то система совершает нерегулярные колебания (рис.4.1, рис.4.2), а при начальных условиях, удаленных от нуля, система -  диссипативна (рис.5.1, рис.5.2). Изменение начальных условий  при малой амплитуде возбуждающей силы не влияет на динамику системы, система - диссипативна, нерегулярные колебания отсутствуют.

Рис.4.1 - Фазовый портрет системы ДУ (2) - (3). Начальные условия: x(0)=0.1, x’(0)=-0.3. Амплитуда вынуждающей силы, А=1.3

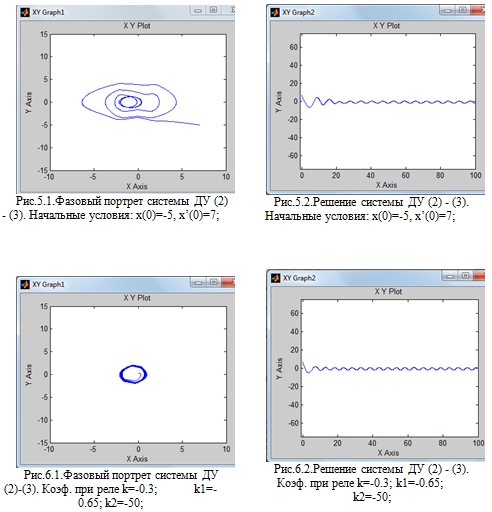
Рис.5.1 - Фазовый портрет системы ДУ (2) - (3). Начальные условия: x(0)=-5, x’(0)=7. Амплитуда вынуждающей силы, А=0.4

 

Анализ поведения системы при изменении коэффициентов при реле

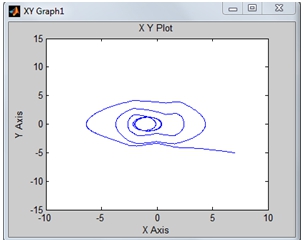
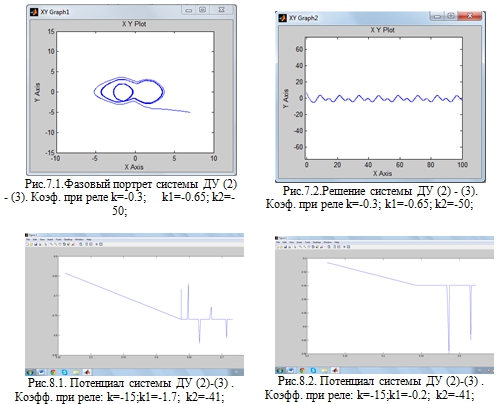
Следующий этап - тестирование при изменении коэффициентов при реле. Проведенные исследования показали, что изменение значений коэффициентов при реле не влияет на возникновение в системе нерегулярных колебаний  (рис.6.1, рис.6.2, рис.7.1, рис.7.2), траектория остается в ограниченной области, система диссипативна.

 

Рис.6.1 - Фазовый портрет системы ДУ (2) - (3). Коэф. при реле k=-0.3; k1=-0.65; k2=-50;

Рис.7.1 - Фазовый портрет системы ДУ (2) - (3). Коэф. при реле k=-0.3; k1=-0.65; k2=-50;

 

Оценка потенциала системы

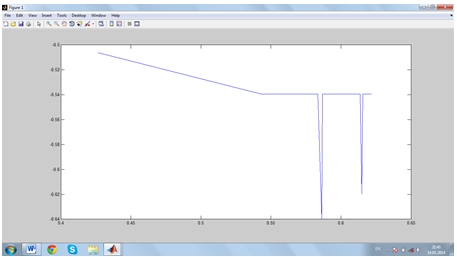
Потенциал рассматриваемой системы можно записать в виде (4):

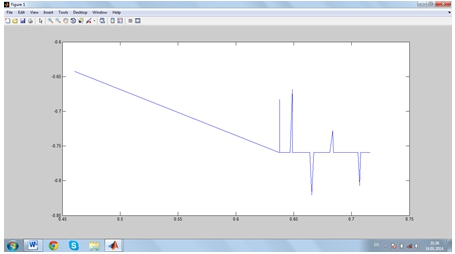
Заключительным этапом исследования была оценка потенциала системы при изменении значений управляющих параметров системы. По итогам тестирования было установлено, что при увеличении амплитуды вынуждающей силы и коэффициентов при реле значение потенциала растет, кол-во “ям” уменьшается (рис. 8.1, рис.8.2).

Рис.8.1 - Потенциал системы ДУ (2)-(3) . Коэффициенты при реле: k=-15;k1=-1.7; k2=-41;

 

Рис.8.2 - Потенциал системы ДУ (2)-(3) . Коэффициенты при реле: k=-15;k1=-0.2; k2=-41;

Заключение

Проведенные исследования показали, что наличие нерегулярных колебаний  в системе или, наоборот, детерминированное (диссипативное) поведение системы, а также вопрос об устойчивости нулевого решения системы зависит от значений управляющих параметров. По итогам исследования были получены следующие результаты:

1. При малых значениях амплитуды вынуждающей силы на длительных временах (в диапазоне значений 0.01 –  0.5 ) система диссипативна (рис.1.1, рис. 1.2), с увеличением амплитуды (в диапозоне 0.6 – 1.3) в системе возникают нерегулярные колебания (рис.2.1, рис. 2.2), в диапозоне (1.7 - 5) система диссипативна(рис.3.1, рис.3.2).
2. Изменение начальных условий при малой возбуждающей силе не влияет на динамику системы, система - диссипативна, нерегулярные колебания отсутствуют. При большой амплитуде система чувствительна к начальным условиям: если начальные условия заданы в окрестности нуля, то система совершает нерегулярные колебания (рис.4.1, рис.4.2), а при начальных условиях, удаленных от нуля, система -  диссипативна (рис.5.1, рис.5.2).
3. Изменение значений коэффициентов при реле не влияет на возникновение в системе нерегулярных колебаний (рис.6.1, рис.6.2, рис.7.1, рис.7.2).
4. При увеличении амплитуды вынуждающей силы и коэффициентов при реле значение потенциала растет, кол-во “ям” уменьшается (рис. 8.1, рис.8.2).
5. Нулевое решение системы ДУ (1)-(2) не устойчиво по Ляпунову, но устойчиво по Лагранжу - траектория остается в ограниченной области, система - диссипативна.

 

Литература

1. Гласс Л., Мэки М. От часов к хаосу: Ритмы жизни: Пер. с англ. – М.: Мир, 1991. – 248с.
2. Анищенко B.C. Сложные колебания в простых системах: механизмы возникновения, структура и свойства динамического хаоса в радиофизических системах. – М.: Наука, 1990. – 312с.
3. Гуляев В.И., Завражина Т.В., Завражина Н.М. Универсальные закономерности зарождения хаотических движений нелинейных механических систем. – К.: ВИПОЛ, 1999. – 135с.
4. Мун Ф. Хаотические колебания. – М.: Мир, 1990. – 312с.
5. Неймарк Ю.И.,Ланда ПС. Стохастические и хаотические колебания. – М.: Наука, 1987. – 424с.
6. Ueda Y. Survey of Regular and Chaotic Phenomena in Forced Duffing Oscillator/ Y. Ueda. 1991. –30с.
7. Байге Х. Детерминированный хаос и сегнетоэлектричество / Байге Х., Дистельхорст М., Дрождин С.Н.// Материалы семинаров научно образовательного центра «Волновые процессы в неоднородных и нелинейных средах». – Воронеж, 2003. – С.9 -22.
8. Никитина Н.В. Нелинейные системы со сложным и хаотическим поведением траекторий. – К.: Издательство Феникс, 2012. – 240с.
9. Красносельский M.А., Покровский А.В. Системы с гистерезисом. – М.: Издательство Наука. Главная редакция физико-математической литературы, 1983. – 272с.
10. Корректные периодические режимы в системах управления с монотонными гистерезисными нелинейностями/Семенов М.Е., Канищева О.И., Прохоров Д.М, Гулин А.Н.// Наукоемкие технологии. – 2010. – № 12. – С. 67-72.
11. Семенов М. Е.  О континуумах вынужденных устойчивых периодических режимов в системах управления./Семенов М.Е.// Автоматика и телемеханика. – 1994. – № 8. –  С.95-98
12. Покровский А.В. Устойчивые периодические режимы в системах с монотонными нелинейностями/ Покровский А.В., Семенов М.Е.// Автоматика и телемеханика. – 1990. – № 2. – С. 31-37
13. Зоны устойчивости и периодические решения перевернутого маятника с гистерезисным управлением/ Матвеев М.Г., Семёнов М.Е., Шевлякова Д.В., Канищева О.И.// Мехатроника, автоматизация, управление. – 2012. – № 11. – С. 8-14.
14. Семенов М.Е. Оптимальное управление в задаче о выборе производственной и ценовой стратегии/ Семенов М.Е., Лебедев Г.Н., Матвеев М.Г.// Системы управления и информационные технологии. – 2009. – № 4. – С. 71.
15. Еременко Ю.И. Об условиях применения ПИД-нейрорегулятора для управления объектами, описываемыми апериодическим звеном второго порядка с запаздыванием / Еременко Ю.И., Полещенко Д.А., Глущенко А.И. // Приборы и системы. Управление. Контроль. Диагностика. – 2013. – №6.  – С. 39-45.
16. Еременко Ю.И. Анализ методов реализации схемы нейросетевого управления с самонастройкой/ Еременко Ю.И., Полещенко Д.А., Глущенко А.И.// Приборы и системы. Управление. Контроль. Диагностика. – 2012. - №6. – С.50-55