ФУНКЦИЯ ИМПУЛЬСНОГО ОТКЛИКА ПОТЕНЦИАЛА ДЕЙСТВИЯ В НЕРВНОМ ВОЛОКНЕ
Понетаева Е.Г.1, Богатов Н.М.2, Григорьян Л.Р.3, Богатов Н.Е.4, Богатов Е.М.5, Щербаков А.С.6
1Аспирант, Кубанский государственный университет; 2Доктор физико-математических наук, профессор, Кубанский государственный университет; 3Кандидат физико-математических наук, доцент, Кубанский государственный университет; 4Магистрант, Кубанский государственный университет; 5 Магистрант, Кубанский государственный университет; 6 Магистрант, Кубанский государственный университет
ФУНКЦИЯ ИМПУЛЬСНОГО ОТКЛИКА ПОТЕНЦИАЛА ДЕЙСТВИЯ В НЕРВНОМ ВОЛОКНЕ
Аннотация
Проанализировано поведение импульсного сигнала при его распространении в нервном волокне. Сигнал бесконечно малой длительности на входе аксона имеет вид асимметричного импульса в пространственном и временном сечениях аксона. Максимум импульса уменьшается, а ширина увеличивается с увеличением пространственной координаты и времени.
Ключевые слова: нервное волокно, импульсный сигнал, функция импульсного отклика.
Ponetaeva E.G.1, Bogatov N.M.2, Grigoryan L.R.3, Bogatov N.E.4, Bogatov E.M.5, Csherbakov A.S.6
1Postgraduate student, Kuban State University; 2Doctor in Physics and mathematics, Professor, Kuban State University; 3PhD in Physics and mathematics, associate professor, Kuban State University; 4Master student, Kuban State University; 5Master student, Kuban State University; 6Master student, Kuban State University
IMPULSE RESPONSE FUNCTION OF THE ACTION POTENTIAL IN NERVE FIBER
Abstract
Behavior of the impulse signal was analyzed during the propagation process in the nerve fiber. An infinitesimal duration signal which is used as an axon input value has a view of asymmetrical impulse in space and time cross section. The maximum of pulse decreases and width of signal increases when coordinate and time increase.
Keywords: nerve fiber, impulse signal, impulse response function.
Regular functioning of the living organism is impossible without the exchange of information between its subsystems. One of the ways of information transfer is propagation of electrical impulses in the nerve fiber. Electric character of nerve pulses is proved in researches done by Hodgkin A.L., Huxley A.F. and others [1-3].
Modeling of bioelectrical effects is widely used in modern electrophysiology to study the processes occurring in living electroexcitable structures [4-7]. Soliton model of nerve fiber transmembrane potential change occurring in process of excitation propagation was developed in works [8-11]. Accurate analytical solution of nerve impulse propagation within Hodgkin-Huxley’s model, based on the integral Laplace transformation and Efros theorem when the input excitation pulse deviates from the Heaviside step function was obtained in [12].
Simulated results are generally consistent with the experimental data. Applied problems, e.g. bioprosthetics, require a solution of a general problem: an analysis of changes of arbitrary signals in nerve fiber. The problem of action potential propagation in nerve fiber for arbitrary input pulses was successfully solved in [13].
The aim of this research is to calculate the impulse response function of the action potential in nerve fiber.
Action potential is the change of the membrane potential between intracellular medium and extracellular substance, which moves with nerve signal propagation, when nerve cells are excited. Equation (1) described an action potential, V(x,t), propagation in nerve fiber [1].
Error! Objects cannot be created from editing field codes., (1)
where r is a radius of the axon, ra is a resistivity of the axoplasm, Сm is a capacitance per unit area of membrane, rm is a resistivity of membrane material, l is a membrane thickness, the action potential is measured from the resting potential.
We search for the solution of the equation (1) when ![]() meeting next conditions:
meeting next conditions:

 and denote
and denote
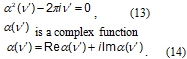 We can find imaginary part of
We can find imaginary part of 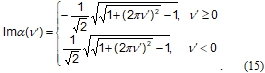 Similarly, we can find the real part of
Similarly, we can find the real part of The equation (15) shows that ![]() is an odd function of
is an odd function of ![]() and the equation (16) shows that
and the equation (16) shows that ![]() is an even function. We will have a solution of the equation (10) with
is an even function. We will have a solution of the equation (10) with ![]() for input arbitrary excitation pulse
for input arbitrary excitation pulse ![]() if we insert (14 – 16) to the (11).
if we insert (14 – 16) to the (11).
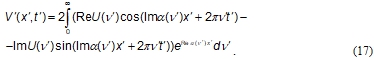
Let ![]() , where
, where ![]() is delta function. We denote the corresponding solution of (17) as
is delta function. We denote the corresponding solution of (17) as ![]() and name it impulse response function. From (12) we have
and name it impulse response function. From (12) we have ![]() then:
then:
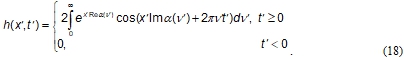
According to the Plancherel theorem, for arbitrary input excitation impulse ![]() we have:
we have:
![]() (19)
(19)
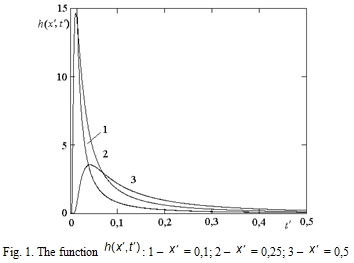
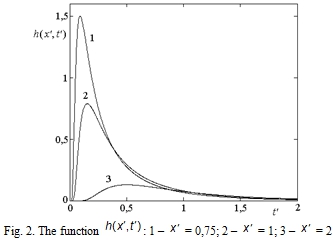
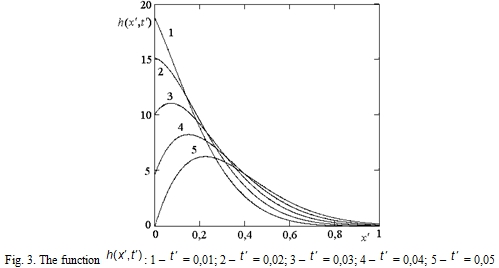
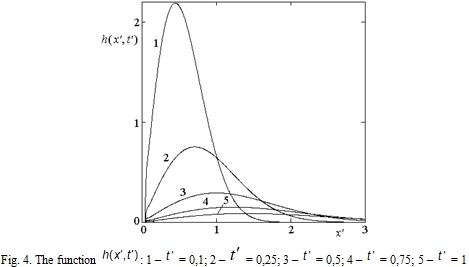
Fig. 1 – 4 show the function changes with different argument values. The function for x' = const is shown in Fig. 1 and Fig. 2. The function for t' = const is shown in Fig. 3 and Fig. 4.
Behavior of the impulse signal was analyzed during the propagation process in the nerve fiber. An infinitesimal duration signal ![]() which is used as an axon input value has a view of asymmetrical impulse in space and time cross section. The maximum of pulse decreases and width of signal increases when x' and t' increase.
which is used as an axon input value has a view of asymmetrical impulse in space and time cross section. The maximum of pulse decreases and width of signal increases when x' and t' increase.
References
- Hodgkin A. L., Rushton W. A. H. The electrical constants of a crustacean nerve fiber // Proc. Roy. Soc. London. 1946. Ser B. V. 133. P. 444-479.
- Hodgkin A. L., Huxley A. F. A quantative description of membrane current and its application to conduction and excitation in nerve // J. Physiol. (London). 1952. V. 117. N4. P. 500-544.
- Hodgkin A.L. Nerve impulse. М.: Mir, 1965. 128 с. (Rus)
- Frankenhaeuser В., Huxley A. The action potential in the myelinated nerve fibre of Xenopus Laevis as computed on the basis of voltage clamp data // J.Physiol. 1964. N P. 302-315.
- Fomin S.V., Berkinblit M.B. Mathematical problems in biology. М.: Nauka, 1973. 200 с. (Rus)
- Abbott L. F., Kepler Т. B. Model neurons: from Hodgkin-Huxley to Hopfield // Statistical Mechanics of Neural Networks, L. Garrido, ed., no. 368 in Lecture notes in Physics, Springer-Verlag, 1990. P. 5-18.
- Dominique Debanne. Information processing in the axon // Nature Reviews Neuroscience. V.5. N4. P. 304-316.
- Maksimenko E.V. The analytical model of the nerve impulse // Obozrenie prikladnoy i promishlennoy matematiki. Т. 10. Vol.3. pp. 696-697. (Rus)
- Maksimenko E.V. The Korteweg-de Vries equation using for transmembrane potential modeling in nerve fiber // Vestnik Severo-Kavkazskogo gosudarstvennogo tehnicheskogo universiteta, seriya «Estestvennonauchnaya». №1(7). pp. 234-235. (Rus)
- Maksimenko E.V. The nerve impulse propagation modeling with computer using // Obozrenie prikladnoy i promishlennoy matematiki. Т. 11. Vol.2. pp.368-369. (Rus)
- Maksimenko E.V. About mathematical methods using in biological researches // Obozrenie prikladnoy i promishlennoy matematiki. Т. 12. Vol. 2. pp. 431-432. (Rus)
- Selezov I.Т., Morozova L.V. Generalization of the action potential excitation and propagation in nerve fiber problem // Prikladna gidrimehanika. Т. 12. N. 3. pp. 75-83. (Ua)
- Bogatov N.М., Grigoryan L.R., Ponetaeva E.G. The modeling of electrical impulses propagation in nerve fiber // Collective monograph. Sovremennie problemy fiziki, biofiziki i infokommunikacionnyh tehnologiy. Krasnodar: Krasnodarskiy CNTI, 2012. pp. 33 – 44. (Rus)