CFD-МОДЕЛИРОВАНИЕ ОМЫВАНИЯ ПОВЕРХНОСТИ ТРУБ УДОБООБТЕКАЕМОЙ ФОРМЫ С НЕПОЛНЫМ ПОПЕРЕЧНЫМ ОРЕБРЕНИЕМ
Письменний Е.Н.1, Рогачов В.А.2, Баранюк А.В.3, Семеняко А.В.4, Вознюк М.М.5
1,2,3,4,5Национальный технический университет Украины Киевский политехнический институт
CFD-МОДЕЛИРОВАНИЕ ОМЫВАНИЯ ПОВЕРХНОСТИ ТРУБ УДОБООБТЕКАЕМОЙ ФОРМЫ С НЕПОЛНЫМ ПОПЕРЕЧНЫМ ОРЕБРЕНИЕМ
Аннотация
В статье рассматривается возможность снижения гидродинамического сопротивления секций теплообменных аппаратов путем применения новых видов развитых конвективных поверхностей нагрева на основе плоско-овальных труб с неполным поперечным оребрением, разработанных в НТУУ «КПИ» .
Ключевые слова: гидродинамическое сопротивление, омывание, отрывное течение, верификация.
Pis'mennij E.N.1, Rogachov V.A.2, Baranyuk A.V.3, Semenyako A.V.4, Voznyuk M.M.5
1,2,3,4,5National technical university of Ukraine is the "Kiev polytechnic institute"
CFD-MODELING OF FLOW NEAR-BY THE SURFACE OF TUBES OF THE COMFORTABLE-SHAPED FORM WITH INCOMPLETE FINING
Abstract
In the article possibility of decline of hydrodynamic resistance of sections of heat-exchange vehicles is examined by application of new types of the developed convectiv surfaces of heating trivial-oval tubes with incomplete transversal fining developed in NTUU «KPI».
Keywords: hydrodynamic resistance, that can be torn off flow, verification.
Введение
Проблема интенсификации теплообмена в конвективных поверхностях нагрева из которых состоит теплообменная секция теплообменного аппарата (ТОА) имеет особую актуальность, которая заключается в минимизации затрат на прокачку теплоносителя через ТОА и одновременным уменьшением его массогабаритных показателей.
Для решения этой проблемы в НТУУ «КПИ» предложено в качестве элементов теплообменной поверхности использовать плоско-овальные трубы удобообтекаемой формы с неполным поперечным оребрением [1-3]. Такие трубы по сравнению с широко применяемыми круглыми оребренными трубами при одинаковых затратах мощности на прокачку теплоносителя имеют на 10-15% большую тепловую эффективность. Аэродинамическое сопротивление шахматных пучков плоско-овальных труб в 1,3-1,4 раза меньше, чем для таких же по геометрическим характеристикам пучков из оребренных круглых труб. Поэтому, для углубления представлений о механизме и причинах интенсификации теплообмена, уровне турбулизации течения в новых типах поверхностей целесообразно использовать методы CFD-моделирования.
CFD-модель позволит детализировать характер течения вблизи несущей трубы и ребер, а также объяснить ожидаемый эффект интенсификации теплообмена оребренной плоско-овальной трубы. Для проверки адекватности численной модели, необходимо провести ее верификацию на известных экспериментальных данных [1]. После чего станет возможным, не проводя дорогостоящих экспериментов, определить оптимальные геометрические характеристики несущей плоско-овальной трубы и ее оребрения.
Постановка задачи
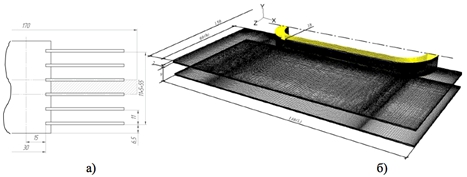
CFD-модель базируется на полной трехмерной модели элемента плоско-овальной трубы с плоским приварным оребрением (рис. 1). Поставленная задача является внешней. Представленная на рис. 1а изучаемая поверхность, размещена в канале аэродинамической трубы прямоугольного сечения. Тонкими осевыми линиями выделен исследуемый элемент поверхности. Расчетный элемент выбран таким образом, чтобы смоделировать гидродинамическую картину течения жидкости в полуоткрытых каналах прямоугольной формы, образованных ребрами и криволинейной поверхностью несущей трубы. С этой целью выбран средний по высоте плоско-овальной трубы межреберный канал.
Для подготовки численной модели использовался пакет CFD-моделирования ANSYS-Fluent. Расчетная область (рис. 2б) покрывалась неравномерной, со сгущением к стенкам трубы декартовой сеткой. Размер минимального шага у стенки трубы выбирался согласно рекомендаций [6] из условия Red-1. Минимальный и максимальный шаги при этом составляли 5×10-5 и 1×10-4 м. Максимальное количество ячеек необходимое для дискретизации составило ~4 млн.
Рис. 1 – Область решения задачи (а) и конечно-элементная модель плоско-овальной трубы (б)
Методика проведения исследований подробно описана в опубликованных ранее работах [1-4].
Результаты верификации CFD-модели
Для проверки адекватности воспроизведения и точности предлагаемой CFD-модели основных аэродинамических характеристик потока проведены исследования распределения статического давления вдоль поверхности ребра, которые представлены в виде безразмерных коэффициентов давления и вычисляемые с помощью соотношения:
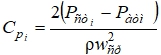 (1)
(1)
где Ратм – атмосферное давление; Рст i – статическое давление в i-м сечении; wср – среднерасходная скорость потока; – плотность омываемого воздуха.
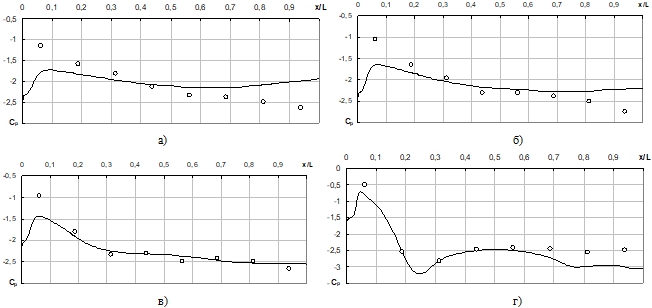
Продольное распределение коэффициентов давления Cpi при разных относительных высотах ребра y/h показано на рис. 2. Анализ представленных ниже данных свидетельствует, что CFD-модель достаточно корректно отражает поле давлений в прикорневой области ребра (y/h = 0,875) и вблизи центра канала (y/h = 0,625). Максимальное отклонение расчетных данных от экспериментальных (по краям кривой) составляет 20%. Но в сечениях y/h = 0,125 и y/h = 0,375, находящихся вблизи вершин ребер, корреляция носит только качественный характер, что связано, по нашему мнению, с недостаточной детализацией расчетной области.
Рис. 2. – Распределение безразмерных коэффициентов давления при Redэ = 50×103 в сечениях y/h = 0,125 (а), y/h = 0,375 (б), y/h = 0,625 (в) и y/h = 0,875 (г): точки – эксперимент; линии – численное моделирование
При этом, необходимо отметить, что при помощи численного моделирования для всех сечений y/h получены данные, которые не обнаружены в физическом эксперименте [3]. Так, область обратного положительного градиента давления вблизи передней кромки ребра x/L » 0,05 (рис. 2) вязана с возникновением на поверхности ребра отрывного пузыря, примыкающего к его острой кромке [9]. Второй и меньший по величине градиент давления, наблюдаемый ниже по потоку только в сечении y/h = 0,875 (рис. 2, г), свидетельствует о наличии отрывной области, находящейся на поверхности несущей трубы в месте, где скругленный ее участок переходит в линейный, так называемый начальный участок.
Резюмируя полученные результаты по верификации, можно констатировать, что разработанная CFD-модель достаточно хорошо воспроизводит закономерности распределения коэффициентов Срi и может быть применена для проведения дальнейших исследований теплогидродинамических процессов при омывании плоско-овальной трубы.
Результаты моделирования гидродинамического процесса
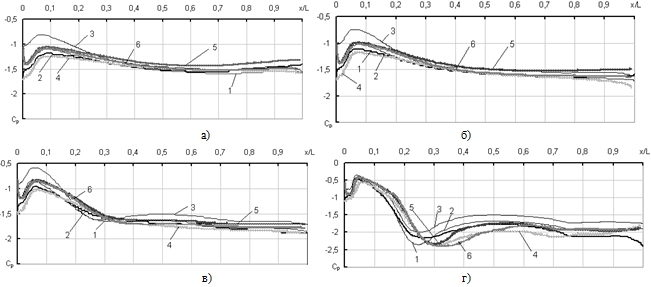
Продольные распределения коэффициентов Cpi на ребре при Redэ = 50×103 и различных относительных удлинениях d2/d1 представлены на рис. 3.
1 –h = 60 мм (d2/d1 = 2,8); 2 –h = 45 мм (d2/d1 = 2,8); 3 –h = 60 мм (d2/d1 = 2,8);
4 –h = 60 мм (d2/d1 = 2); 5 –h = 45 мм (d2/d1 = 2); 6 –h = 30 мм (d2/d1 = 2).
Рис. 3. – Распределение коэффициентов Cpi вдоль ребра в сечениях y/h = 0,125 (а), y/h = 0,375 (б), y/h = 0,625 (в) и y/h = 0,875 (г)
Анализ рис. 3 свидетельствует, что зависимости Cpi = f(x/L) имеют немонотонный характер, указывающий на постепенный рост скорости внутри межреберного канала. В интервале 0,125 ≤ y/h ≤ 0,875 на участке 0 ≤ x/L ≤ 0,05 (вблизи передней острой кромки ребра) наблюдается стремительное падение, а затем постепенный рост давления, до максимума, координаты которого практически совпадают с координатами отрывного пузыря, примыкающего к кромке ребра (рис. 3). Второй градиент давления прослеживается на всех кривых для сечения y/h ≤ 0,875 (рис. 3, г), расположенного ближе к корню ребра. Причем, минимумы давлений малоподвижны и не зависят от высоты ребра h. Их координата для профиля трубы d2/d1 = 2,8 составляет x/L » 0,23, а для трубы d2/d1 = 2,0 –x/L » 0,3.
На рис. 4 по результатам моделирования представлена картина течения на поверхностях ребра и несущей трубы в виде траекторий движения частиц потока. Численный эксперимент позволил получить первую отрывную зону, примыкающую к передней кромке ребра. Напомним, что толщина ребра в данных исследованиях имеет 2 мм, а она по оценкам работ [8, 9] существенно влияет на длину отрывной зоны, которая для указанной толщины составляет ~ 7 мм. Этот результат подтверждается вычислительным экспериментом в котором длина отрывной зоны для различных Redэ и y/h является величиной фиксированной и равной x » 0,05L, где L = 140 мм.
Отрывной пузырь 1 деформирован (растянут вдоль по потоку) со стороны свободного торца ребра и около „кармана”, размещенного между выступающими частями ребер вблизи лобовой части трубы. Логично допустить, что деформация отрывного пузыря связана в первую очередь с взаимодействием потоков, которые двигаются в образованных ребрами полуоткрытых каналах. Таким образом, вблизи стенки трубы существует две замкнутые отрывные области. Длина второго отрывного пузыря 2 составляет ~ 7 мм , а его высота в средней части ~ 1,4 мм. Дальше за точкой присоединения на стенке трубы начинает развиваться пограничный слой, срыв которого происходит в кормовой части за миделевым сечением закругленного участка трубы и переходит в ближний след 3, который обычно формируется позади тел цилиндрической формы и носит циркуляционный характер. Представленная на рис. 3 схема течения в качественном отношении похожа на схему течения в межреберных каналах плоско-овальных труб, полученную по результатам экспериментальных исследований методом визуализации [3].
Резюмируя представленные результаты, можно констатировать, что с помощью вычислительного эксперимента удалось более полно описать закономерности течения в межреберных каналах плоско-овальных труб с неполным поперечным оребрением и объяснить механизм интенсификации теплообмена в них [4].
Выводы
По результатам численного моделирования можно сделать следующие выводы:
- верификация с экспериментальными данными [1] показала, что различия между расчетными и опытными коэффициентами давления, в среднем, не превышают 18 %;
- численный расчет расширил представления об особенностях течения на ребре плоско-овальной трубы и позволил получить модель течения на поверхностях трубы и ребра.
Литература
- Письменний Е.Н., Терех А.М., Семеняко А.В., Баранюк А.В. Теплоаэродинамическая эффективность трубчатых поверхностей нагрева ре-генераторов ГТУ // Промышленная теплотехника. – 2010. – Т.32, №4 – С. 63-73.
- Письменний Е.Н., Терех А.М., Бурлей В.Д., Баранюк А.В. Теплообмен и аэродинамическое сопротивление малорядных пучков плоско-овальных труб с неполным оребрением // Промышленная теплотехника. – 2010. – Т.32, №5 – С. 34-41.
- Семеняко А.В., Письменный Е.Н. Течение на поверхности плоско-овальных труб с поперечным оребрением // Труды XVII школы-семинара молодых ученых и специалистов под руководством академика РАН А.И. Леонтьева. – 25-29 мая. – г. Жуковский, Россия. – 2009. – Т.2. – С. 132-135.
- Письменный Е.Н., Рогачов В.А., Баранюк А.В., Семеняко А.В., Вознюк М.М. CFD-моделирование процессов теплобмена труб удобообтекаемой формы с неполным поперечным оребрением // Международный научно-исследовательский журнал. – 2014. – №1 (20) – С. 30-36.
- Быстров Ю.А., Исаев С.А., Кудрявцев Н.А., Леонтьев А.И. Численное моделирование вихревой интенсификации теплообмена в пакетах труб – Санкт-Петербург: Судостроение, 2005. – 389 с.
- Мочалин Е.В., Халатов А.А. Гидродинамика закрученного потока в ротационных фильтрах – Институт технической теплофизики НАН Украины. – Киев, 2010. – 428 с.
- Краус А. Охлаждение электронного оборудования – Л.: «Энергия», 1971. – 246 с.
- Эпик Э.Я. Проблемы прогнозирования и расчета верхнего теплового ламинарно-турбулентного перехода (проблемный доклад) // Труды V Минского международного форума по тепло-и массообмену, 24-28 мая 2004,-Минск.-2004.-10 с.
- Сперроу Е., Кер Н. Влияние неравномерного распределения скорости на входе на турбулентный теплообмен и потери давления в плоско-паралельном канале прямоугольного сечения // Теплопередача – 1983 – т.105, №3 – С.100-109.