Разработка адаптивного алгоритма определения характеристик продольного режима ПОЛЕТА летательных аппаратов

Обеспечение управляемости БПЛА с учётом погрешности параметрической оценки выступает актуальной проблемой интеграции автоматизированных систем, существующих на современном этапе. Такой процесс осуществляется, учитывая весовой разброс, неточность данных параметрических характеристик продольного режима работы БПЛА. Для того чтобы компенсировать весовой разброс посредством классических положений формирования системы управляемости БПЛА с цифровой надстройкой контура управления, нужно применять коэффициенты, отражающие обратные и прямые взаимосвязи составляющих. В данном случае это способствует сокращению резерва устойчивости БПЛА в ходе их движения, а также колебаний инженерно-технической конструкции, увеличению скорости отклонений управленческих компонентов.

В целях решения обозначенной проблемы целесообразно применить на практике адаптивный алгоритм определения параметрических характеристик продольного режима работы БПЛА. Они не предполагают наличие полного объёма информации о системе управления при начальных изменениях и условиях функционирования БПЛА. Это реализуется при помощи подстраивания параметрических системных характеристик на базе информационных данных, которые собираются в ходе совершения полета.

Цель исследования – сформировать адаптивный алгоритм определения характеристик продольного режима работы летательных аппаратов.

Задачи исследования:

1. Осуществить постановку задачи адаптивного управления продольным режимом полета летательных аппаратов.

2. Представить результаты формирования адаптивного алгоритма определения характеристик продольного режима работы летательных аппаратов.

3. Отразить результаты сравнительного анализа и изучения работоспособности адаптивного алгоритма определения характеристик продольного режима работы летательных аппаратов.

Объект исследования – БПЛА.

Предмет исследования – управление продольным режимом работы летательных аппаратов на примере БПЛА.

Научная новизна исследования:

1. Осуществлена постановка задачи адаптивного управления продольным режимом полета летательных аппаратов с формированием структуры адаптивного управления, сочетающей применение априорных данных и текущих результатов выявления параметрических характеристик БПЛА.

2. Создан адаптивный алгоритм определения характеристик продольного режима полета летательных аппаратов, способствующий стабилизации корней полиномиальной модели на фоне модификации рекурсивной концепции метода наименьших квадратов.

Практическая значимость данного исследования состоит в том, что приведенный адаптивный алгоритм определения параметрических характеристик продольного режима работы летательных аппаратов может быть применен для совершенствования процедур текущей идентификации параметрических характеристик продольного режима работы БПЛА различных моделей.

Обзор литературных источников

К управлению высотой и скоростью БПЛА в академическом сообществе представлен общепринятый подход, который подразумевает, что высота и скорость как характеристики продольного режима управления БПЛА разделены. При использовании контроллеров высота БПЛА управляется рулём, а скорость – тяговым стабилизатором.

Одной из актуальных задач в национальной гражданской авиации выступает оптимизация управления высотой и скоростью БПЛА, что отмечено различными авторами

Во второй половине предыдущего столетия возник подход к управлению полетом БПЛА, базирующийся на манипулировании кинетической и потенциальной энергией. Ключевые концептуальные положения подобного алгоритма приведены в работах

На базе подхода к управлению полетом БПЛА, основанного на манипулировании кинетической и потенциальной энергией, были протестированы контроллеры на примере разных типов БПЛА в сфере управления полетом

В ходе исследования процессов управления и эффективности систем полета БПЛА различными авторами были созданы математические модели. Так, в статье В.А. Федулова, Н.В. Быкова, В.Д. Баскакова представлена математическая модель, позволяющая оценить эффективность системы, поражающие вражеские БПЛА. Математическая модель была сформирована на основе принципов имитационного моделирования

В статье

Поскольку полная математическая модель движения БПЛА крайне трудная в практической реализации, целесообразно её упростить при помощи концептуальных моделей управления режимом полета БПЛА, приведенных в монографиях

В статье А.В. Рысина, В.Н. Бойкачёва, Я.Б. Островского представлены принципы преобразования линейных систем управления БПЛА к форме в соответствии с каноническим подходом

Научное исследование, проведенное А.А. Воеводой, Ю.П. Филюшовым, В.Ю. Филюшовым, ориентировано на практическое осуществление современных программно-аппаратных средств с целью имплементации алгоритма управления траекторией движения БПЛА. Авторы применили современные вычислительные пакеты и прикладное обеспечение для формирования оптимальной траектории полета БПЛА

Возможность разработки смешанного адаптивного подхода к управлению продольным режимом полета БПЛА была высказана в исследовании

Математическое моделирование продольного режима работы БПЛА осуществляется при помощи уравнения движения, которое может учитывать ключевые факторы управления летательными аппаратами. Интеграция адаптивного алгоритма была обусловлена практическим применением концепции продольного режима работы БПЛА, которая позволяет учесть нелинейность параметрических характеристик. Воздействие возмущений ветра описывалось на базе гипотезы о постепенном охвате ветром БПЛА. Посредством введенного коэффициента Sкр учитывалось влияние на вращение БПЛА по крену при малых углах.

На рисунке 1 проиллюстрирована схема задачи адаптивного управления продольным режимом работы летательных аппаратов.

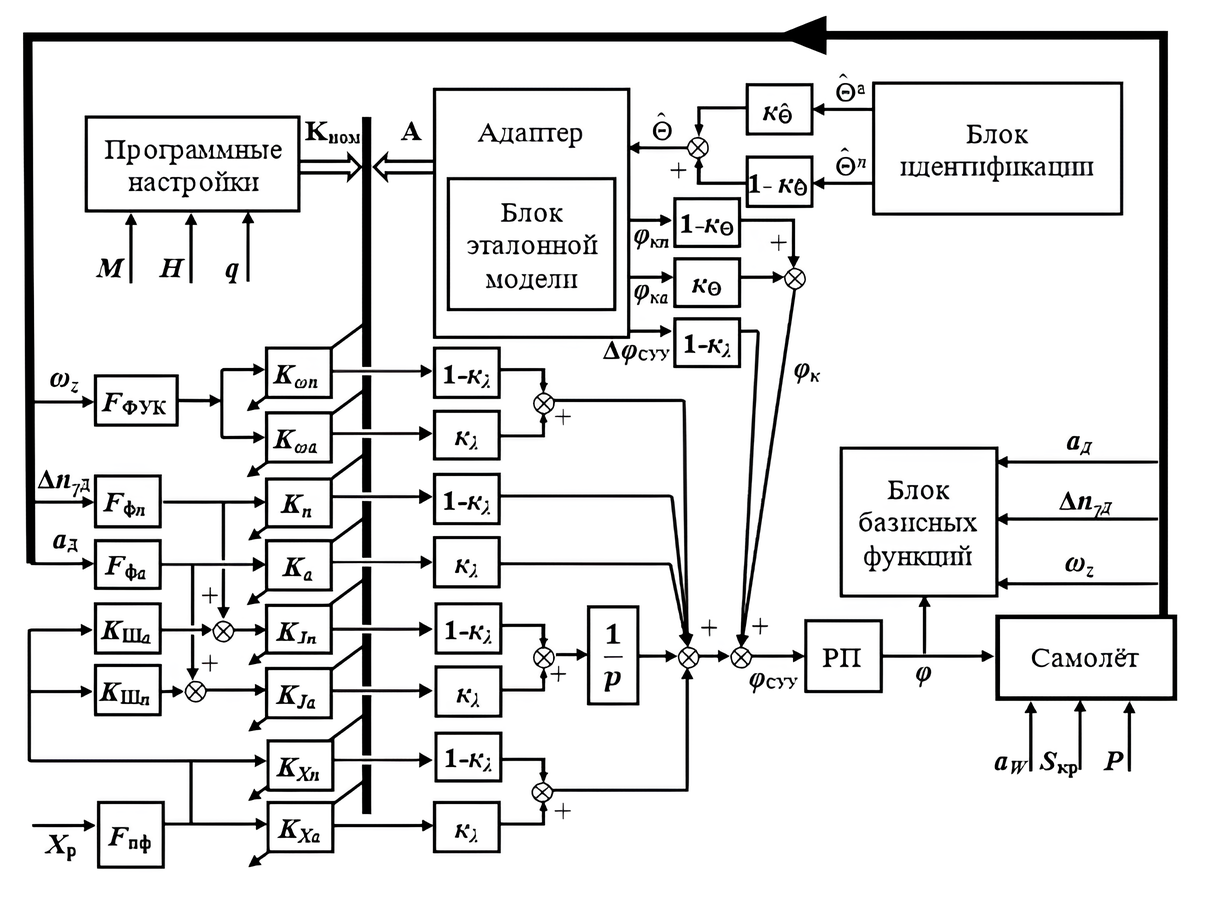
Рисунок 1 - Схема задачи адаптивного управления продольным режимом полета летательных аппаратов

DOI:10.60797/IRJ.2025.152.7.1

По сравнению с классическими системами управления продольным режимом работы БПЛА адаптивный алгоритм подразумевает работу адаптера (элемент адаптации системы), определение параметрических характеристик продольного режима работы БПЛА. Исходя из оценки параметрических характеристик продольного режима работы БПЛА, элемент адаптации системы выявляет корректировки коэффициентов, адаптирующих систему, с помощью которых обеспечивается эталон математической модели. Передаточные показатели (при общем обозначении K) представляют собой совокупность номинальных уровней цифровых надстроек, корректировки коэффициентов, адаптирующих систему.

Информационная база научного исследования – данные результатов трубных продувок БПЛА, параметрические инерционные характеристики продольного режима работы.

Авторский адаптивный алгоритм определения характеристик продольного режима полета летательных аппаратов включает в себя совокупность стадий:

1. Анализ имеющихся способов адаптации управленческой системы при использовании продольного режима полета БПЛА на основе существующих академических работ

Наиболее результативным может быть беспоисковый способ адаптации управленческой системы при использовании продольного режима полета БПЛА.

2. Определение текущей динамики БПЛА в рамках адаптивного алгоритма.

3. Приближение текущей динамики БПЛА к модели эталона продольного режима полета.

Модель эталона можно рассматривать в качестве звена III порядка, о чём свидетельствует формула (1):

(1)

Приведенный эталон соответствует передаточной модели БПЛА как замкнутой системы с адаптивным управлением продольным режимом полета, не учитывая силу тяжести фильтров и стабилизатора БПЛА. Для того чтобы динамическое изменение эталонной модели соответствовало колебаниям, нужно компенсировать коэффициент , обозначающий апериодический корень, который определяется астатизмом адаптивного управления, нулевым значением общего знаменателя p. Параметрические характеристики модели эталона отобраны таким образом, что значения  и  положительные, но не более 4 баллов.

4. Проведение сравнительного анализа двух методических подходов к формированию адаптивного алгоритма определения характеристик продольного режима полета летательных аппаратов.

Первый методический подход к формированию адаптивного алгоритма определения характеристик продольного режима полета летательных аппаратов базируется на устойчивости уровней коэффициентов, входящих в замкнутую систему математических уравнений, исходя из модели эталона. Приведенное утверждение обозначено в формулах (2), (3):

(2)

(3)

По причине фильтрации обратных взаимосвязей  обладает наиболее высоким порядком по сравнению с. Присутствует ограничение по количеству параметрических характеристик продольного режима работы БПЛА. Соответственно, целесообразно поддерживать адаптивный алгоритм согласно модели эталона. Для того чтобы это сделать, характеристика  была приведена к виду, обозначенному в формуле (4):

(4)

Затем целесообразно приравнять параметры полинома в формуле (4) к параметрическим характеристикам, выделенным в формуле (2). Тогда формируется система математических уравнений. Её решение – корректировки адаптивной системы продольного режима полета БПЛА.

Второй методический подход к формированию адаптивного алгоритма определения характеристик продольного режима полета летательных аппаратов базируется на достижении устойчивости изменения доминирующих характеристик D(p): комплексно-сопряженной пары коэффициентов и параметра p1. Тогда выражение D(p) нужно преобразовать таким образом, чтобы каждому передаточному коэффициенту соответствовала полиномиальная функция. Например, это приведено в формуле (5):

(5)

Если известны значения DЭ(p), pэ1, pэ2, формируется система математических уравнений. Её решение – корректировки адаптивной системы продольного режима полета БПЛА. Это обозначено в формуле (6):

(6)

При этом корректировка адаптивной системы продольного режима полета БПЛА Axa(n) определяется так, чтобы соблюдалось равенство . Формула (7) непосредственного вычисления приведена ниже:

(7)

Второй методический подход к формированию адаптивного алгоритма определения характеристик продольного режима полета летательных аппаратов является основным в проведении научного исследования, поскольку по сравнению с первым рассмотренным методическим подходом обеспечивается устойчивость доминирующих коэффициентов согласно заданным числам. Кроме того, объединение адаптивного алгоритма с автоматизированной системой показало, что второй методический подход к формированию адаптивного алгоритма определения характеристик продольного режима полета летательных аппаратов наиболее эффективен.

5. Оценка параметрических характеристик продольного режима полета БПЛА.

Решение подобной задачи лежит в основе осуществления текущей идентификации параметрических характеристик. Анализ нескольких научно-исследовательских трудов

В процессе реализации научного исследования был использован методический подход, в рамках которого упрощена рекурсивная концепция МНК, однако все параметрические характеристики структурно соответствуют между собой. В авторском методическом подходе к анализу текущей идентификации использована концепция линейного моделирования с насыщением двух характеристик: f(ε) и λ.

Следовательно, изменения параметрических характеристик адаптивной системы управления продольным режимом работы БПЛА определяются в рамках формулы (8):

(8)

где λ – характеристика, вычисляемая по формуле (9):

(9)

f(ε) – характеристика, вычисляемая по формуле (10):

(10)

Можно отметить, что производная выбранной функции будет с наибольшей вероятностью положительной по математическому знаку. Изменения параметрических характеристик адаптивной системы управления продольным режимом работы могут определяться линейно независимыми параметрами, которые по своему значению отличны от нуля, тогда адаптивный алгоритм будет стабильным с асимптотической точки зрения, поскольку решение, полученное в рамках математического уравнения ε, принимающее нулевое значение, не будет выступать направлением адаптивного алгоритма.

– ожидаемое значение при выявлении оценки идентификации характеристик;

– оценка идентификации;

ε – ошибка.

Расчёт оценок параметрических характеристик в ходе идентификации подразумевает реализацию таких стадий, как:

1) фильтрация корректируемых параметрических характеристик;

2) выявление модели базисной функции;

3) расчёт текущей оценки параметрических характеристик;

4) сглаживание полученного решения;

5) расчёт первоначальной совокупности оценок моментных и силовых параметрических характеристик.

Использовались две моментные характеристики:  и  с учётом влияния на БПЛА с адаптивным механизмом управления продольным режимом полета, учитывая возмущения ветра и возможные вращения аппарата по крену (см. табл. 1).

Масштаб полученной оценки, в первую очередь, определяется в ситуации малой амплитуды движения БПЛА, так как полученные значения практически соответствуют ожидаемым. Воздействие на степень точности расчётов при выявлении текущего состояния относительной погрешности крайне низкое. Кроме того, относительная погрешность оценки параметрической характеристики, обусловленной наличием ветра, соответствует полученным расчётам, не воздействует на интеграцию адаптивного алгоритма управления продольным режимом полета БПЛА.

При управлении продольным режимом полета БПЛА решение математической модели может быть не единственным. Тем не менее, при синтезе параметрических характеристик решение математической модели единственное, оно достаточное для практического применения в адаптивном алгоритме управления продольным режимом полета БПЛА, обеспечивает стабилизацию движения БПЛА в условиях адаптивного управления.

Особенности формирования адаптивного алгоритма определения характеристик продольного режима полета БПЛА, выбор критериев для создания модели эталона, выявление критериев скорости работы стабилизатора БПЛА позволили проанализировать интеграцию адаптивного алгоритма определения характеристик продольного режима полета БПЛА при осуществлении полета с одинаковой скоростью. При сравнении режима работы БПЛА без и с адаптивным алгоритмом определения характеристик продольного режима работы было отмечено, что практическое применение авторского алгоритма комплекс корней и астатический корень находятся рядом с уровнями модели эталона с учётом весовых разбросов (см. рис. 2, 3).

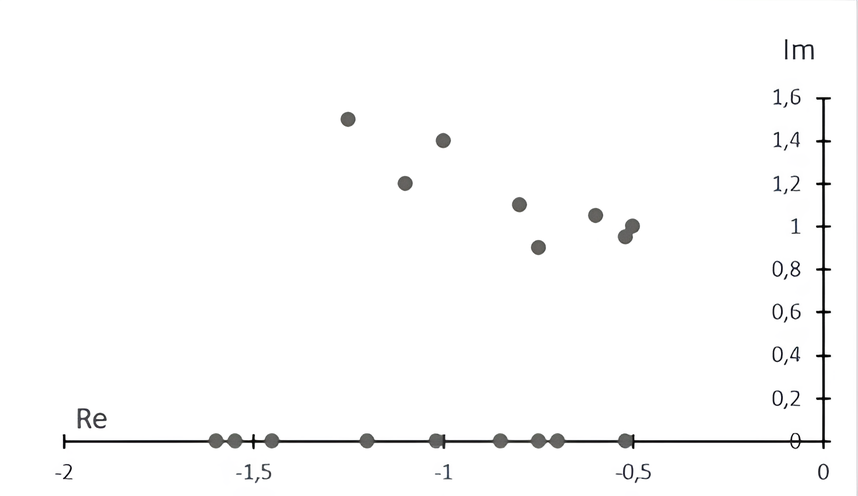
Рисунок 2 - Исследование режима работы БПЛА без применения адаптивного алгоритма определения параметрических характеристик продольного режима полета

DOI:10.60797/IRJ.2025.152.7.3

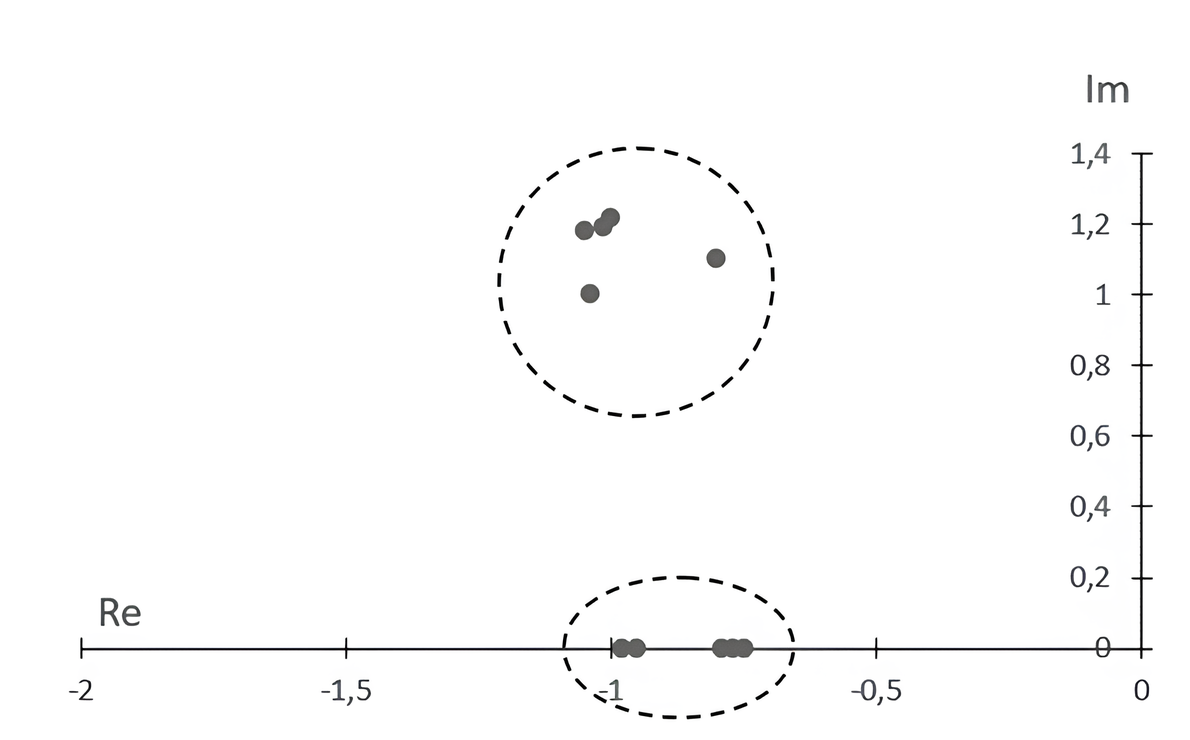
Рисунок 3 - Исследование режима работы БПЛА с применением адаптивного алгоритма определения параметрических характеристик продольного режима полета

DOI:10.60797/IRJ.2025.152.7.4

Практическое использование векторных сигналов при управлении продольным режимом полета способствовало обеспечению устойчивости комплекса корней и астатического корня в некоторой ограниченной области значений рядом с уровнями модели эталона. В данном случае это гарантирует высокую степень качества динамики летательных аппаратов.

При анализе переходных процессов в управлении БПЛА при помощи адаптивного алгоритма управления продольным режимом полета было обнаружено, что при малых сигналах отмечается ошибка реакции БПЛА, что возможно при низком значении и недокомпенсированности астатического корня. Анализ обратных взаимосвязей показал, что переходные процессы в управлении БПЛА в рамках настраивания адаптивного алгоритма находятся на приемлемом уровне. Практическое использование адаптивного алгоритма определения параметрических характеристик продольного режима полета БПЛА, учитывая многорежимность аппаратов при весовом разбросе неустойчивости ±2,6%, способствовало обеспечению значительного запаса устойчивости по малой и большой амплитуде.

Работоспособность адаптивного алгоритма определения характеристик продольного режима полета летательных аппаратов исследовалась с точки зрения корректировки скорости движения. Кроме того, были использованы разные маневры БПЛА: торможение, разворот, разгон. На примере каждого из них была достигнута устойчивость и управляемость продольным режимом полета БПЛА, учитывая корректировки скорости движения. Процесс оценки текущей идентификации также был относительно устойчивым.

По сравнению с классическими алгоритмами управления продольным режимом полета БПЛА практическое использование адаптивного алгоритма определения параметрических характеристик продольного режима полета, учитывая многорежимность объектов исследования при весовом разбросе неустойчивости ±2,6%, способствует:

1. Обеспечению значительного запаса устойчивости по малой и большой амплитуде.

2. Уменьшению скорости стабилизатора летательных аппаратов в два раза.

3. Обеспечению стабильности и управляемости БПЛА при влиянии параметрических характеристик – возмущений, которые определяются скачкообразными изменениями и потенциальным сокращением результативности работы стабилизатора летательных аппаратов.

На основании результатов проведенного научного исследования и вышеизложенного материала были сделаны следующие ключевые выводы в работе:

1. Актуальная проблема исследования: обеспечение управляемости БПЛА с учётом погрешности параметрической оценки в условиях интеграции автоматизированных систем, существующих на современном этапе.

2. Адаптивный алгоритм подразумевает работу адаптера (элемент адаптации системы), определение параметрических характеристик продольного режима полета БПЛА. Исходя из оценки параметрических характеристик продольного режима полета БПЛА, элемент адаптации системы выявляет корректировки коэффициентов, адаптирующих систему, с помощью которых обеспечивается эталон математической модели.

3. Информационная база научного исследования – данные результатов трубных продувок БПЛА, параметрические инерционные характеристики продольного режима полета.

4. Авторский адаптивный алгоритм определения характеристик продольного режима полета летательных аппаратов включает в себя совокупность стадий: анализ имеющихся способов адаптации управленческой системы при использовании продольного режима полета БПЛА на основе существующих академических работ; определение текущей динамики БПЛА в рамках адаптивного алгоритма; приближение текущей динамики БПЛА к модели эталона продольного режима работы; проведение сравнительного анализа двух методических подходов к формированию адаптивного алгоритма определения характеристик продольного режима работы летательных аппаратов: по результатам был выбран второй методический подход, поскольку по сравнению с первым рассмотренным методическим подходом обеспечивается устойчивость доминирующих коэффициентов согласно заданным числам; оценка параметрических характеристик продольного режима полета БПЛА.

5. По сравнению с классическими алгоритмами управления продольным режимом полета БПЛА практическое использование адаптивного алгоритма определения параметрических характеристик продольного режима работы, учитывая многорежимность объектов исследования при весовом разбросе неустойчивости ±2,6%, способствует обеспечению значительного запаса устойчивости по малой и большой амплитуде; уменьшению скорости стабилизатора летательных аппаратов в два раза; обеспечению стабильности и управляемости БПЛА при влиянии параметрических характеристик – возмущений, которые определяются скачкообразными изменениями и потенциальным сокращением результативности работы стабилизатора летательных аппаратов.