АНАЛИТИЧЕСКИЕ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО С ПАРАМЕТРАМИ

АНАЛИТИЧЕСКИЕ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО С ПАРАМЕТРАМИ

Научная статья

Алыбаев К.С.^1, *, Нарымбетов Т.К.²

¹ ORCID: 0000-0002-7962-534X;

² ORCID: 0000-0003-0921-4542;

^{1, 2} Жалал-Абадский государственный университет, Жалал-Абад, Киргизская Республика

* Корреспондирующий автор (alybaevkurmanbek[at]rambler.ru)

Аннотация

В данной работе рассматриваются аналитические  функции комплексного переменного с малыми параметрами порождаемые некоторыми операторами. Исследуется асимптотическое поведение функции, по малому параметру. Задача решена с использованиям линии уровня гармонических функции. Область аналитичности функции разделяется некоторыми линиями на части и в некоторых частях пределы (по малому параметру) существуют, а в других бесконечны или не существуют.

Ключевые слова: Аналитические функции; отображения пространств; линии уровня; параметры; пути интегрирования.

ANALYTICAL FUNCTIONS OF AN COMPLEX VARIABLE WITH PARAMETERS

Research article

Alybaev K.S.^1, *, Narymbetov T.K.²

¹ ORCID: 0000-0002-7962-534X;

² ORCID: 0000-0003-0921-4542;

^{1, 2} Jalal-Abad State University, Jalal-Abad, Kyrgyz Republic

* Corresponding author (alybaevkurmanbek[at]rambler.ru)

Abstract

In this paper, we consider the analytic functions of a complex variable with small parameters generated by some operators. We study the asymptotic behavior of a function with respect to a small parameter. The problem is solved using line-level harmonic functions. The analytic domain of the function is divided by some lines into parts, and in some parts the limits (by a small parameter) exist, but in others they are infinite or do not exist.

Keywords: analytical functions; display spaces; level lines; options; integration paths. 

Введение

Теория функций комплексного переменного имеют многочисленные приложения для решения задач гидро-аэродинамики, теории упругости, электростатистики, магнитных и тепловых полей и т.д.  Следовательно развитие теории функций комплексного переменного для разработки новых методов решения различных математических и практических задач является актуальной. 

Обозначения и вспомогательные понятия

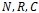• - соответственно множество натуральных, действительных и комплексных чисел;
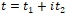•  - комплексная переменная, где  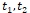- действительные переменные; ;
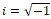• ε - малый положительный вещественный параметр, если функция зависит от ε“по ε” будет обозначать ;
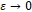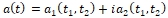•  - комплекснозначная функция комплексной переменной, где  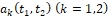вещетвеннозначные функции двух вещественных переменных;
•  - односвязная область в том смысле, что две любые ее точки можно соединить спрямляемой кривой;
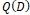•  - пространство аналитических комплекснозначных функций в D;
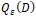• - пространство аналитических комплекснозначных функций в D с параметром ε;
• Множество 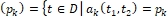 называется линией уровня функции  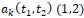в области D;
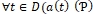•  - означает:  для любого t из D функция a(t) обладает свойством P:

Постановка задачи

Рассмотрим пространство 

Определение 1. Если  для любого  найдется  такое, что при  (или на кривой p)  имеет место неравенство

то будем говорить, что  стремится при   к функции  равномерно относительно t в области D  (или на кривой c).

Далее согласно принятого определения исследуем задачу  В частности к таким задачам сводятся исследование асимптотического поведения решений сингулярно возмущенных обыкновенных дифференциальных  уравнений или систем в комплексных областях.

Решение поставленной задачи для произвольной функции комплексной переменной практически является неразришимой. Ограничимся рассмотрением некоторых аналитических функций комплексного переменного.

Пусть заданы пространства   и оператор   переводящий элемент пространства  в элемент пространства .

Если  

Представление аналитических функций на линиях

Справедливо утверждение: Гармонические функции принимают  каждое свое значение на некоторых линиях (линиях уровня) и совпадают с постоянными на линиях будучи торжественно не равными постоянной.

Функция z(t) в целом на линии (p) представляется в виде

, причем в каждой точке  функция  принимает значение p согласно утверждения. Выражение  означает значение функции    в некоторой точке .

В нащих дальнейщих исследованиях при рассматрение аналитических функций на линиях будем учитывать такие представления.

Решения задачи для некоторых операторов

Пусть  скалярная функция.

I. Определим оператор . Пусть  и её внутренняя точка, и выполняется следующее условие: 

Из условия  вытекает, функция  в области D не имеет кратных точек и t₀ является простым нулем функции  [1,2,3].

Область D полностью покрывается взаимно ортогональными линиями уровней функций 

Для внесения ясности в топологию области D в терминах линии уровня введем в рассмотрение линию . В силу условия   такая линия существует. Линия  проходит через точку t₀ и область D делит на части  где выполняются соотношения  причем выполнения  одновременно в двух областях исключается. Для определенности возьмём , причем равенства имеет место только на линии

Рассмотрим следующие случаи:

1. Пусть t произвольная точка принадлежащая 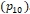. Рассмотрим функцию

Функция  принимает значение 0.

Отсюда вытекает для функции  в рассматриваемой точке  не существует, но она ограничена по модулю. Точка t произвольная из  не существует, но она ограничена по модулю.

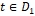2.  Введем на рассмотрение линию

и область, ограниченную линиями  обозначим , а оставшуюся часть D₁ обозначим D₁₁. Линию  отнесем к области D₁₁.

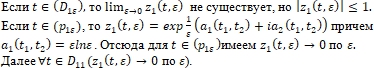
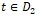3. . Рассмотрим линии

Область ограниченную линиями  обозначим  оставшуюся часть D₂ обозначим D₂₁. Линию  отнесем к области D₂₁. Далее, если  не существует, но по мере приближения t к линии   Примечание. Если условие U заменить на следующее.

то линия  в точке  разветвляется и области D разделяет на  частей, причем ровно в  областях (содержащие ветви ) предел   по ε не существует, а в n областях . Такие области чередуются. К примеру 

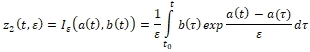II. Пусть    (1)

Пусть выполняются условия:

Как и в предыдущем случае определим линию  и области .

Для исследования функции  по ε определим пути интегрирования. Согласно U2 функция . Следовательно пути интегрирования можно выбрать произвольными, но полностью принадлежащими D.  Если , то путь состоит из части  соединяющую точки .

Если , то путь состоит из части  соединяющую точки  и части линии соединяющую точки . Линии  порождаемые гармоническими функциями,  являются аналитическими кривыми и их уравнения можно представит параметрически . В качестве параметра возьмём длины кривых . Пусть  длина кривой  отчитываемого  точки t₀ до точки. Уравнение кривой  представим в виде

где  текущие координаты точек принадлежащие кривым . С учетом выбранных путей интегрирования и их параметрическое представление,  (1) представим в виде

 

В (4) интеграл в правой части имеет порядок ε. Следовательно  не имеет предела по ε, но ограничена по модулю.

Пусть .  Из (2), интегралы в правой части проинтегрировав по частям, получим

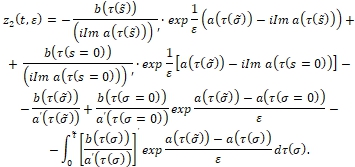   (5)

В , а интеграл имеет порядок ε. Для значений  имеем  Тогда 

Пусть .  Рассмотрим линию . Линией  область D₂ разделяется на части . Если линия

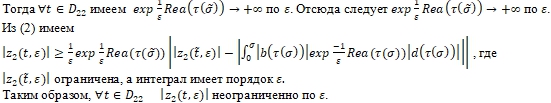
III. Рассмотрим векторные аналитические функции комплексного переменного.

Определение. Пусть   то будем говорить, что  векторная аналитическая функция комплексного переменного с компонентами  .

Пространство таких функций обозначим . Пространство функций  обозначим .

Норму определим так

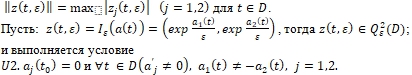
Из U2 вытекает, что функции  не имеют кратных точек и через каждую точку области D проходит единственная линия уровня функций . В отличие от примера I в данном случае область D покрывается линиями уровней двух пар  и это затрудняет описание топологии области D в терминах линии уровня. Но согласно U2 линии

пересекаются в точке

В общем случае линии  могут иметь несколько точек пересечения отличных от t₀ и определить такие точки практически невозможно.

Для наглядности предположим:

U3. Линии  в области D не имеют других точек пересечения, кроме точки t₀.

Тогда в силу  область D линиями  разделяется на четыре части и только в одной части, эту часть обозначим D1, выполняются соотношения.

  причем равенства имеет место только на границе D1, состоящее из частей линии  (рис. 1).

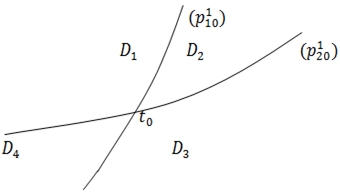
Рис. 1 – Деление области D линиями 

Заметим, если в условии     то линии  совпадают и область D разделяется на две части, при этом не существует область, где одновременно выполняются неравенства 

Линиями уровня  разделим на части  (рис. 2).

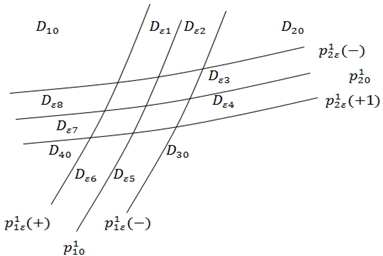
Рис. 2 – Деление областей 

 

Далее исследуем предел

Если учесть результаты I, то

Для областей  не существуют.

IV. Пусть 

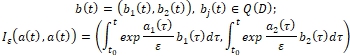
и выполняются условия U2, U3.

Для этого случая, учитывая вычисления проведенные в случаях II, III получим 

а для областей  не существуют.

V. Пусть  скалярные функции;

   (7)

 - константа не зависящая от ε.

Далее будем рассматривать  пространство  с множеством

 некоторая положительная не зависящая от ε}

Пусть выполняется условия U1.

Решим задачу при каких условиях

  с множеством H.

Для решения этой задачи как и в I определим линию и области

В (7) пути интегрирования определим как и в случае  II и используем их параметрическое представление.

Пусть  Тогда из (7) имеем

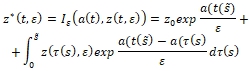   (8)

где 

Поведение интеграла в (8) при , имеющимися сведениями о функции  невозможно определить, но этот интеграл ограничен. Наличие первого слагаемого показывает, в рассматриваемом случае, предел   не существует.

Из (8) переходя к модулю получим

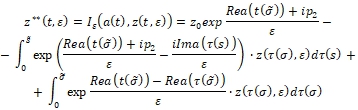где  Отсюда  при    (9) Теперь рассмотрим случай . Для этого случая из (7) имеем     (10) где  В (10) проведем следующее преобразование     (11) В (11) выражение содержащееся в [...] даёт функцию . Учитывая это (11) перепишем в виде   (12) Если  (определена в I), то из (12) вытекает     (13) где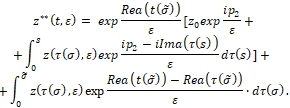 

К интегралу (13), применяя метод интегрирование по частям (функция ) строго монотонна вдоль линии , что и обеспечивает такую возможность) получим

где  некоторая постоянная не зависящая от ε.

Таким образом 

По определению

Отсюда при условии 

Пусть   (11) представим в виде

Если   органичена.

Если   а выражение содержащееся в [...] ограничена по модулю. Следовательно  не ограничена.

Выводы

Таким образом доказано, что аналитические функции (скалярные или векторные) с малыми параметрами обладают рядом специфических свойств. В частности существуют линии делящие области на части и на таких линиях и областях примыкающих к данным линиям пределы функции  по малому параметру не существуют, а в других областях бесконечны или существуют и в последнем случае предельная функция принадлежит к пространству  или

При рассмотрении операторов  отображающих элементы из пространства   только при определенных условиях принадлежит пространству  .

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Евграфов М.А. Аналитические функции / М.А. Евграфов. – Москва: Наука, 1991. - 448 с.
2. Лаврентьев М.А. Методы теории функций комплексного переменного / М.А. Лаврентьев, Б.В. Шабат. – Москва: Наука, 1973. – 739 с.
3. Федорюк М.В. Метод перевала / М.В.Федорюк. – Москва: Наука, 1977. - 368 с.
4. Алыбаев К.С. Метод линий уровня исследования сингулярно возмущенных уравнений при нарушении условия устойчивости / Алыбаев К.С. // Вестник КГНУ. – Серия 3, Выпуск 6. – Бишкек, 2001. – С. 190-200.
5. Алыбаев К.С. Метод погранслойных линий построения регулярно и сингулярных областей для линейных сингулярно возмущенных уравнений с аналитическими функциями /К.С. Алыбаев, К.Б. Тампагаров //Естественные и математические науки в современном мире: сб. статей по материалам XLVII международной научно-практической конференции. № 10 (45). Россия, Новосибирск: СиБАК, 2016. - С.59-66.
6. Шишкова М.А. Рассмотрение одной системы дифференциальных уравнений с малым параметром при высших производных /М.А.Шишкова//Доклады АН СССР. – 1973. - Т. 209, № 3. – С. 576-579.
7. Алыбаев К.С. Построение областей притяжения при вырождении сингулярно возмущенных уравнений /К.С. Алыбаев, А.Б. Мурзабаева // Международный научно-исследовательский журнал. № 9 (75). Екатеринбург, 2018. - С. 7-11.

Список литературы на английском языке / References in English

1. Evgrafov M. A. Analiticheskie funkcii [Analytical functions]/ M. A. Evgrafov. - Moscow: Nauka, 1991. - 448 PP. [in Russian]
2. Lavrentiev M. A. Metody teorii funkcij kompleksnogo peremennogo [Methods of the theory of functions of a complex variable] / M. A. Lavrentiev, B. V. Shabat. - Moscow: Nauka, 1973. – 739 p [in Russian]
3. Fedoryuk M. V. Metod perevala [The method of the pass] / M. V. Fedoryuk. Moscow: Nauka, 1977. - 368 p. [in Russian]
4. Alybaev K. S. Metod linij urovnya issledovaniya singulyarno vozmushchennyh uravnenij pri narushenii usloviya ustojchivosti [Method of level lines of the study of singularly perturbed equations in violation of the conditions of stability] / Alybaev K. S. // Vestnik KNU. - Series 3, Issue 6. - Bishkek, 2001. - Pp. 190-200. [in Russian]
5. Alybaev K. S. Metod pogranslojnyh linij postroeniya regulyarno i singulyarnyh oblastej dlya linejnyh singulyarno vozmushchennyh uravnenij s analiticheskimi funkciyami [Method of boundary-layer lines of regular and singular domains construction for linear singularly perturbed equations with analytical functions] /K. S. Alybaev, K. B. Tampagarov //Natural and mathematical Sciences in the modern world: collection of articles based on XLVII international scientific-practical conference. 10 (45). Russia, Novosibirsk: Sibak, 2016. - Pp. 59-66. [in Russian]
6. Shishkova M. A. Rassmotrenie odnoj sistemy differencial'nyh uravnenij s malym parametrom pri vysshih proizvodnyh [Consideration of one system of differential equations with a small parameter at higher derivatives] /M. A. Shishkova/ / Reports of the USSR Academy of Sciences. - 1973. - Vol. 209, No. 3. - Pp. 576-579. [in Russian]
7. Alybaev K. S. Postroenie oblastej prityazheniya pri vyrozhdenii singulyarno vozmushchennyh uravnenij [Construction of regions of attraction at degeneration of singularly perturbed equations] / K. S. Alybaev, A. B. Murzabaeva / / international scientific research journal. 9 (75). Ekaterinburg, 2018. - Pp. 7-11. [in Russian]