О МЕТРИЧЕСКОЙ СВЯЗНОСТИ ЛЕВИ-ЧИВИТА НА РАСПРЕДЕЛЕНИЕ ПЛОСКОСТЕЙ

О МЕТРИЧЕСКОЙ СВЯЗНОСТИ ЛЕВИ-ЧИВИТА НА РАСПРЕДЕЛЕНИЕ ПЛОСКОСТЕЙ

Научная статья

Омельян О.М.* ORCID 0000-0003-4359-1376, Балтийский федеральный университет им. И. Канта, Калининград, Россия

* Корреспондирующий автор (olga_omelyan2002[at]mail.ru)

Аннотация В n-мерном проективном пространстве исследуется распределение m-мерных плоскостей с заданным метрическим тензором. Рассматривается  объект касательной связности  и показывается, что аффинная распределенная связность может являться обобщенной связностью Леви-Чивита в случае голономного распределения и в случае полунормализованного 1-го рода распределения с соответствующей адаптацией репера. Доказывается, что подобъект касательной распределенной связности  также может быть охвачен полем метрического тензора, но лишь в адаптированном репере.

Ключевые слова: распределение, репер, проективное пространство, метрический тензор, объект связности, обобщенная связность Леви-Чивита, охват.

ON LEVY-CHIVITA METRIC CONNECTIVITY ON DISTRIBUTION OF PLANES

Research аrticle

Omelyan O.M.* ORCID 0000-0003-4359-1376, Kant Baltic Federal University, Kaliningrad, Russia

* Corresponding author (olga_omelyan2002[at]mail.ru)

Abstract

In n-dimensional projective space, the distribution of m-dimensional planes with a given metric tensor is investigated in the paper. The object of tangent connection is considered, and it is shown that the affine distributed connection can be generalized with a Levi-Civita connection in the case of a holonomic distribution and in the case of a semi-normalized distribution of the 1st kind with the corresponding adaptation of the frame. It is proved that the subobject of the tangent distributed connection can also be covered by the field of the metric tensor, but only in the adapter frame.

Keywords: distribution, frame, projective space, metric tensor, connected object, generalized Levi-Civita connection, coverage.

В проективном пространстве P_n рассмотрим распределение   m-мерных плоскостей P_m  с заданным метрическим тензором g. На распределении плоскостей рассмотрим касательную распределенную связность с объектом  компоненты которого удовлетворяют сравнениям [1, C.179] по модулю базисных форм {wⁱ, w^a}. Эта связность содержит аффинную связность с подобъектом  _,  обобщающую классическую аффинную связность без кручения на поверхности. Возникает вопрос: может ли касательная распределенная связность быть связностью Леви-Чивита, то есть существует ли охват компонент объекта касательной связности с помощью метрического тензора g и его пфаффовых производных? Следует отметить, что компоненты g_ij дважды ковариантного тензора g удовлетворяют условиям

Продолжая уравнения (1), получим сравнения для пфаффовых  производных компонент метрического тензора g по модулю базисных форм w¹

Пусть компоненты объекта аффинной связности симметричны, то есть кручение В этом случае из сравнений [1, C. 180] для компонент объекта аффинной связности естественно предположить, что трехиндексные формы симметричны по нижним индексам, то есть  а значит распределение является голономным, либо Проциклируем  сравнения (2₁) для пфаффовых производных g_ijkпо индексам  i, j, k.

В систему (3) подставим  выражения  трехиндексных форм из  [1]  и, учитывая симметрию метрического тензора, вычтем последнее сравнение из суммы двух первых

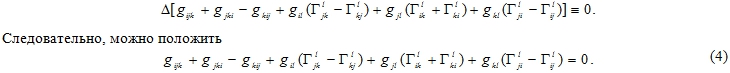
Будем рассматривать голономное распределение . С учетом симметрии компонент аффинной распределенной связности по нижним индексам  получаем, что (4) преобразуется к виду:

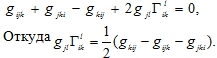Меняя индексы соответствующим  образом и  учитывая, что у метрического тензора g_ij существует обратный тензор g^ij, связанный с ним следующим соотношением, получаем                 Замечание 1 При выводе формулы (5) мы использовали условие симметрии форм а не условие голономности распределения из которого автоматически вытекает симметрия форм  . Следовательно, формула (5) справедлива лишь при условии, что формы  симметричны по нижним индексам. Формулу (5) также можно получить при адаптации репера нормализации 1-го рода неголономного распределения. Для этого запишем деривационную формулу репера для точек   в виде: Произведем оснащение распределения к каждой точке  A присоединим плоскость дополнительной  размерности P_n-m. Тогда из уравнений (6) видно, что если , то: то есть сравнения  являются условиями относительной инвариантности плоскости P_n-m = [A, A_a]. Выражения для трехиндексных форм в репере, адаптированном нормализации 1-го рода, принимают вид:   Тогда обращаясь к системе (3) и используя равенство вытекающее и  выражений (7) для трехиндексных форм, можно получить очевидное сравнение

Подставляя в эти сравнения выражения для трехиндексных форм из [1], получаем равенство (4), откуда следует формула (5). Теорема 1 Аффинная связность с подобъектом компоненты которого определяются по формуле (5), является обобщенной связностью Леви-Чивита на голономном распределении и на полунормализованном 1-го рода неголономном распределении . Замечание 2 Объект  с помощью метрического тензора g и его пфаффовых производных по формуле (5), совпадающей с формулой, определяющей связность Леви-Чивита на поверхности.

Предположим, что компоненты объекта линейной подсвязности несимметричны, то есть кручение Так как любую двухиндексную величину можно представить в виде суммы симметричной и антисимметричной частей, то

Подставляя равенства (8) в (4), получим Используя формулу (8), имеем

Теорема 2 На неголономном распределении аффинная связность с подобъектом  компоненты которого определяются формулой (9), порождается полем метрического тензора g и объектом кручения S. Замечание 3 Из формулы (9) следует формула (5) при условии, что S=0. Обратимся теперь к подобъекту касательной распределенной связности. В адаптированном нормализации 1-го рода репере, уравнения [1, C. 179] упрощаются Сравнения (3₂) для пфаффовых производных g_ija метрического тензора принимают вид:

Свернем сравнение (10) с тензором в результате получим Так как то Следовательно, можно положить _. Введем обозначение  тогда с учетом   то есть.

Теорема 3 На полунормализованном 1-го рода распределении  в адаптированном репере существует порожденная полем метрического тензора касательная распределенная подсвязность с подобъектом  компоненты которого определяются по формуле (11). Установим принципиальное различие понятий обобщенной связности Леви-Чивита ­и индуцированной связности. При исследовании распределения плоскостей обнаружилось 2 способа определения  касательной  распределенной  связности с объектом _.  1. индуцирование связности оснащающим квазитензором λ [2, C. 64]; 2.порождение связности метрическим тензором g. Возникает очевидный вопрос: существует ли связь между этими двумя способами определения связности? Запишем выражения объекта касательной распределенной связности Г с помощью оснащающего квазитензора λ причем сравнения для компонент оснащающего квазитензора λ имеют вид [2, C. 64].  Для того чтобы найти зависимость между g и λ, мы в соответствии с условиями пунктов 3–5, рассмотренных выше, приравняем  правые части  выражений  охватов для объекта связности Г. Во-первых,  приравняем (12) и (5)

Свернем выражения (13) по индексам i и j

Теорема 4 Если индуцированная аффинная связность 1-го типа  совпадает с обобщенной  связностью Леви-Чивита    голономного распределения   и полунормализованного 1-го рода распределения  то оснащающий подквазитензор  является функцией (14), то есть нормализация 1-го рода распределений  и  порождает нормализацию 2-го рода.

Во-вторых, приравняем (12) и (9) Сворачивая выражения (15) по индексам i и j, получаем

Теорема 5 Если индуцированная аффинная связность 1-го типа  совпадает со связностьюпорождаемой полем метрического тензора и объектом кручения неголономного распределения то оснащающий подквазитензор λ_k является функцией (16), то есть нормализация 1-го рода и объект кручения распределения  порождают нормализацию 2-го рода. И наконец, приравняем (12) и (11), получим

Свернем (17) по i и j Теорема 6 Если индуцированная касательная подсвязность 1-го типа  совпадает с обобщенной связностью Леви-Чивита полунормализованного распределения , то оснащающий подквазитензор λ_a является функцией (18), то есть метрика распределения  порождает оснащение Картана, подчиненное нормализации 1-го рода. Вывод Итак, в общем случае формулы (14, 16, 18) не имеют места, поэтому определение касательной  распределенной  связности с объектом  на распределении NS_n с помощью оснащающего квазитензора λ, либо с помощью метрического тензора g есть два разных способа задания связности. В первом случае говорят об индуцированной связности 1-го типа, а во втором случае будем говорить об обобщенной связности Леви-Чивита.

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы/ References

1. Омельян О. М. Об объекте кривизны групповой связности на распределении плоскостей / О. М. Омельян // Тр. мат. центра им. Н.И. Лобачевского. –Казань, 2002. –Т. 18. – С. 69.
2. Омельян О. М. Понятие связности Леви-Чивиты, обобщенное на распределение плоскостей / О. М. Омельян  // Тр. мат центра им. Н.И. Лобачевского. – Казань, 2003. –Т. 21. – С. 179 - 180.
3. Омельян О. М. Четыре индуцированных связности на распределении плоскостей / О. М. Омельян // Тр. межд. конф. по геометрии и анализу. – Пенза, 2003. – С. 63 - 69.
4. Омельян О. М. Обобщение связности Леви-Чивита на распределение плоскостей / О. М. Омельян // Диф. геом. многообр. фигур. –Калининград, 2004. –№ 35. –С. 105 – 113.
5. Омельян О. М. Теоретико-категорный подход, естественно расширяющий фундаментальное понятие связности, и его приложение к геометрии дифференциальных систем / О. М. Омельян, Л. Е. Евтушик // Фундаментальная и прикладная математика. – Москва, 2010. – Т. 16.– Вып.1. – С. 55 – 63.
6. Омельян О. М. О совпадении групповых связностей, индуцированных внутренним композиционным оснащением распределения / О. М. Омельян // Матем. заметки. – Москва, 2017. Т. 102:6. – С. 896–907.
7. Евтушик Л. Е. Дифференциально-геометрические структуры на многообразиях / Л. Е. Евтушик, Ю. Г. Лумисте, Н. М. Остиану и др. // Пробл. геом. / ВИНИТИ. ¾ М., 1979. ¾ Т. 9. ¾ С. 5 – 247.
8. Лаптев Г. Ф. Распределения касательных элементов / Г. Ф. Лаптев // Пробл. геом. / ВИНИТИ. – М., 1971. – Т. 3. – С. 29 – 48.
9. Лаптев Г. Ф. Распределения m-мерных линейных элементов в пространстве проективной связности. I / Г. Ф. Лаптев, Н. М. Остиану // Тр. геом. семин./ ВИНИТИ. ¾М., 1971. ¾ Т. 3. ¾ С. 49 – 94.
10. Остиану Н. М. Распределения m-мерных линейных элементов в пространстве проективной связности. II / Н. М Остиану // Тр. геом. семин. / ВИНИТИ. – М., 1971. –Т. 3. – С. 95 – 114.