ОПРЕДЕЛЕНИЕ КАСАТЕЛЬНЫХ СИЛ ПУЧЕНИЯ ПРИ ТЕПЛОМАССОПЕРЕНОСЕ В ОКРЕСТНОСТИ ОДИНОЧНОЙ СВАИ

ОПРЕДЕЛЕНИЕ КАСАТЕЛЬНЫХ СИЛ ПУЧЕНИЯ ПРИ ТЕПЛОМАССОПЕРЕНОСЕ В ОКРЕСТНОСТИ ОДИНОЧНОЙ СВАИ

Научная статья

Попов В.И.*

Институт горного дела Севера им. Н.В. Черского Сибирского отделения Российской академии наук, Якутск, Россия

* Корреспондирующий автор (popov.gtf[at]mail.ru)

Аннотация

На основе решения задачи совместного тепломассопереноса, в рассматриваемой области определены температура, влагосодержание, льдосодержание, а также концентрация растворенных в жидкой фазе солей, негативно действующих на процессы замерзания. В зонах достаточного увлажнения порового пространства при замерзании развиваются значительные касательные напряжения. На основе введения пространственных элементов -ледяных включений (шлиров) с известным раскрытием, определяемым из решения задачи тепломассопереноса организован переход к расчету напряженно-деформированного состояния в системе мерзлый грунт – свая в рамках упругой постановки. Представлены результаты моделирования процесса формирования сил морозного пучения возле заглубленной сваи на основе двумерной математической модели тепломассопереноса.

Ключевые слова: тепломасооперенос, свая, пучение, касательные силы пучения.

DETERMINATION OF TANGENTIAL HEAVING FORCES UNDER HEAT AND MASS TRANSFER IN THE VICINITY OF A SINGLE PILE

Research article

Popov.V.I.*

Chersky Institute of Mining of the North SB RAS, Yakutsk, Russia

* Corresponding author(popov.gtf[at]mail.ru)

Abstract

The temperature, moisture content, ice content, as well as the concentration of salts dissolved in the liquid phase, adversely affecting the freezing processes, are determined in the considered region on the basis of solving the problem of joint heat and mass transfer. Significant shear stresses develop in the zones of sufficient moistening of the pore space during freezing. The transition to the calculation of the stress-strain state in the frozen soil, pile as part of the elastic formulation, was organized on the basis of introducing spatial elements of ice inclusions (slits) with a known disclosure determined from the solution of the heat and mass transfer problem. The results of the simulation of the forces formation of frost heaving near a recessed pile on the basis of a two-dimensional mathematical model of heat and mass transfer are presented.

Keywords: heat and mass transfer, pile, heaving, tangential heaving forces.

Введение

Негативное воздействие морозного пучения на горнотехнические сооружения в период промерзания грунтов является основной причиной их деградации, начиная с момента строительства и в течение всего периода их эксплуатации [1, C. 12], [2, C. 15], [3, C. 204] . Совокупное влияние температуры среды, состояния поверхности грунта и распределение его параметров по глубине, включая распределения влажности и льдистости а также их динамика создают сложный спектр причин ответственных за формирование условий морозного пучения оснований [4, C. 51], [7, C. 5]. Большинство методов расчета сил морозного пучения промерзающих и оттаивающих оснований базируется, в основном, на решении задачи теплопереноса и определении амплитудных значений границы промерзания - протаивания грунтов оснований [8, C. 5], [9, C. 37], [10, C. 4].

Применение методов численного моделирования поведения сооружений позволяет контролировать по этапам процессы изменения температурно-влажностных полей и связанных с ними деформаций, а следовательно прогнозировать эффективность использования различных материалов и мероприятий для снижения или исключения негативных явлений, действующих на свайные фундаменты и грунты оснований в условиях их сезонного промерзания-оттаивания. Пошаговое решение строится следующим образом, сначала рассматривается задача тепломассопереноса, в результате решения которой, определяются поля концентрации, влагосодержания - (w) и льдосодержания - (Lod) на каждом шаге по времени, затем определяется степень заполнения порового пространства льдом и при достижении определенного критерия решается задача определения плоской картины НДС в мерзлых грунтах основания.

Задача тепломассопереноса

Математическая модель процесса тепломассопереноса при промерзании состоит из системы трех уравнений параболического типа с учетом конвективных членов: уравнения конвективной теплопроводности, диффузионно - конвективного движения влаги и растворенного компонента. Система замыкается уравнением фазового состояния порового раствора Т_F=T_F(w,C), учитывающим специфические характеристики среды - потенциал адсорбционного взаимодействия выраженный через влагосодержание, величину удельной поверхности, концентрацию порового раствора [11, C. 238]. С помощью введения параметра захвата предусмотрена возможность учета селекции растворенного компонента на межфазовой границе лед-рассол.

Решение системы уравнений осуществляется на основе конечно - разностных соотношений полученных с помощью интегро-интерполяционного метода. Применены процедуры расщепления по физическим процессам (конвективный перенос (фильтрация), диффузия, фазовый переход) исходной системы уравнений.

Моделирование тепломассопереноса в системе свая – промерзающий массив в течение годового климатического цикла проведено для случаев отсутствия инфильтрации загрязнения с поверхности и при её наличии. Расчеты проведены для значений; температуры массива Т_мас= –2^оС; температуры рассола Т _рас= –2^оС; начальная концентрация порового раствора в массиве С₀=1 г/л.; концентрации рассола С_рас=100 г/л; начальная влажность массива равна 0,2. Динамика температуры среды теплообмена соответствует годовому циклу. В момент времени t=t_x в течение времени t_инф высокоминерализованный раствор с температурой Т_рас и концентрацией С_рас инфильтруется с поверхности массива в околосвайную область. На поверхности массива происходит конвективный теплообмен с воздушной средой с температурой Т_СР, при этом, потоки влаги и солей в период отсутствия инфильтрации равны нулю. На боковых границах рассматриваемой области ставятся условия равенства нулю потоков тепла, влаги и соли. Так как массив имеет отрицательную температуру то величины содержаний воды, льда и концентрации определяются на основе уравнения фазового равновесия по исходным значениям влагосодержания и концентрации, заданных для талого состояния. Расчетная область имеет размеры 10 м. в глубину и 20.4 в ширину, с центральным расположением бетонной сваи толщиной 0.4 м. и длиной 5.5 м. из которых 5 м. заглублены в грунт основания.

Определение НДС пучения

Учет влияния касательных сил пучения [12, C. 83] на поверхность сваи определяется суперпозицией силового воздействия структурных элементов - «шлиров», ледяных включений прямоугольной формы. При воздействии знакопеременных температур на поверхность массива горных пород в последнем происходят процессы перераспределения влаги и образования льда. Пороговый критерий возникновения условий механического воздействия на поверхность расположенной в массиве фундаментной сваи определяем по заполнению порового пространства льдом на 85% [4, C. 92]. Для численного расчета напряженно-деформированного состояния основания введем размеры «шлиров», как узких включений толщиной d и длиной 2а, с углом ориентации β к горизонтальной оси x главной системы координат. Поле напряжений вокруг «шлира» определяется на основе производящей функции метода разрывных смещений [13, C. 85]:

Используя, полученное из решения задачи тепломассообмена, распределение избыточного льдосодержания в расчетной области и размерные параметры включений перейдем к числовой плотности распределения одинаковых включений в узлах расчетной сетки. Тогда компоненты напряженно деформированного состояния в расчетной области можно представить в виде суперпозиции соответствующих решений для одиночного включения:

а) решения задачи о напряженно деформированном состояния в плоскости с распределенными элементами - «шлирами» и расчет напряжений на граничных элементах представляющих свободную поверхность массива;

б) решения задачи с фиктивными граничными условиями обеспечивающими отсутствие касательных и нормальных напряжений на поверхности массива основания.

Расчет наряжений во внутренних точках расчетной области определяется как

Здесь первый интеграл представляет суммирование вкладов в величину напряжений в теле основания от структурных элементов «шлиров», распределенных по расчетной области S с числовой плотностью P(ρ), второй интеграл представляет вклад граничных элементов на свободной поверхности массива B.

Представленное решение относится к задаче о полуплоскости с распределенными в ней ледяными включениями (шлирами) при этом граница полуплоскости свободна от касательных и нормальных напряжений. Для определения воздействия касательных сил пучения (от роста «шлиров») на основе полученного решения определим эти напряжения на граничных элементах (площадках) вдоль линии раздела сваи и грунта. На (рис. 1) представлены соответствующие результаты.

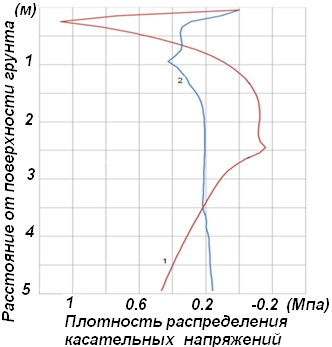
Рис.1 – Распределение касательных сил пучения по длине сваи: 1 – диффузионная модель промерзания, 2 – учет инфильтрационных потоков минерализованного раствора

 

Заключение

Разработана комплексная модель взаимодействия фундаментной сваи с породами основания в условиях промерзания и инфильтрации растворов повышенной концентрации. Инфильтрация минерализованных растворов в зоне расположения фундаментной сваи существенно снижает ее несущую способность.

Представленная модель взаимодействия сваи и промерзающего основания позволяет на ограниченной основе данных о сложении основания и климатических параметров создавать сезонные прогнозы устойчивости свайного фундамента при угрозах техногенного загрязнения грунтового основания.

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Киселев М. Ф. Мероприятия против деформаций зданий и сооружений от действия сил морозного выпучивания фундаментов/ М. Ф. Киселев// М.: Стройиздат.- 1971.- 104 с.
2. Далматов Б. И. Воздействие морозного пучения грунтов на фундаменты сооружений / Б. И. Далматов // Ленинград ; Москва : Госстройиздат. [Ленингр. отд-ние].- 1957. - 60 с.
3. Sritharan S. Effects of seasonal freezing on bridge column-foundation-soil interaction and their implications / S. Sritharan, M. T. Suleiman, D. J. White//.Earthquake Spectra -2007.-23:1. –P. 199-222.
4. Деформации и напряжения в промерзающих и оттаивающих породах. Под ред. Ершова Э. Д. – М.: МГУ.- 1985. - 167с.
5. Qiang L.I. Numerical simulation of pile foundation performance in liqufiable soils with a frozen crust / Liang TANG , Zhaohui YANG , Xianzhang LING// In 5th International Conference on Earthquake Geotechnical Engineering, (January 2011, 10-13, Santiago, Chile) Paper No. NSPYA.
6. Akili W. Stress-strain behavior of frozen fine-grained soils./ W. Akili // Highway Research Record: Frost Action and Drainage. 1971, No. 360: 1-8.
7. Третьякова О. В. Нормальные напряжения морозного пучения как функция избыточной влажности / О.В. Третьякова // Инженерно-строительный журнал. 2017. № 8(76). С. 130–139.
8. Alekseeva O. I. Permafrost engineering in Yakytian geocryological research / O. I. Alekseeva // J. Earth’s Cryosphere. 2017, vol. XXI, No. 4, pp. 3–9.  DOI: 10.21782/EC2541-9994-2017-4(3-9)
9. Тер-Мартиросян З. Г. Расчет касательного напряжения морозного пучения вдоль ствола сваи при учете ее деформируемости / З. Г. Тер-Мартиросян, П. А. Горбачев // Жилищное строительство. -2011. - № 12.- С . 36-39.
10. Сахаров И. И. Решение трехмерной температурно-влажностной задачи промерзания и пучения на примере малоэтажного кирпичного здания / И. И. Сахаров, В. Н. Парамонов, К. Г. Шашкин// Ж. Развитие городов и геотехническое строительство. 2011, Вып. №2, С. 1-12.
11. Попов В. И. Решение задач тепломассопереноса при промерзании – оттаивании горных пород с учетом уравнения фазового состояния поровой влаги/ В. И. Попов, А. С. Курилко //. ГИАБ. – Тематическое приложение «Физика горных пород»,- 2006. С. 236-242.
12. Далматов Б. И. Исследования касательных сил пучения и влияния их на фундаменты сооружений/ Б. И. Далматов// АН СССР: Институт мерзлотоведения, 1954. 29 с.
13. Крауч С. Методы граничных элементов в механике твердого тела/С. Крауч, А. Старфилд //. -М.: Мир. 1987.-328с.

Список литературы на английском языке / References in English

1. Kiselev M. F. Meropriyatiya protiv deformatsiy zdaniy i sooruzheniy ot deystviya sil moroznogo vypuchivaniya fundamentov [Measures against the deformation of buildings and structures from the action of the forces of frosty buckling of the foundations]. M .: Stroyizdat, -1971.- 104p. [in Russian]
2. Dalmatov B. I. Vozdeystviye moroznogo pucheniya gruntov na fundamenty sooruzheniy [The impact of frost heaving of soils on the foundations of buildings] / B. I. Dalmatov// - Leningrad; Moskva: Gosstroyizdat. [Leningr. otd-niye]. -1957. - 60 p. [in Russian]
3. Sritharan, S. Effects of seasonal freezing on bridge column-foundation-soil interaction and their implications ./ S.M. Sritharan, T. Suleymana, D. J. White //. Earthquake Spectra. -2007.- 23: . -P. 199-222.
4. Deformatsii i napryazheniya v promerzayushchikh i ottaivayushchikh porodakh [Deformations and stresses in freezing and thawing rocks]. Pod red. Yershova E. D. - M .: MGU. -1985. – 167p. [in Russian]
5. Qiang L.I., Numerical simulation of pile foundation performance in liqufiable soils with a frozen crust./Liang TANG , Zhaohui YANG , Xianzhang LING// In 5th International Conference on Earthquake Geotechnical Engineering, (January 2011, 10-13, Santiago, Chile) Paper No. NSPYA.
6. Akili W. Stress-strain behavior of frozen fine-grained soils./ W. Akili // Highway Research Record: Frost Action and Drainage.- 1971.- No. 360:-P. 1-8.
7. Tret'yakova O.V. Normal'nyye napryazheniya moroznogo pucheniya kak funktsiya sverkhtochnoy vlazhnosti [Normal frost heats as a function of excess moisture] / O.V. Tret'yakova // Inzhenerno-stroitel'nyy zhurnal. 2017. № 8 (76). P. 130-139. [in Russian]
8. Alekseyeva O.I. Tekhnika vechnoy merzloty v yaktovskikh geokriologicheskikh issledovaniyakh./ O.I. Alekseyeva // Earth’s Cryosphere . 2017, vol. XXI, № 4, P. 3-9. DOI: 10.21782 / EC2541-9994-2017-4 (3-9)
9. Ter-Martirosyan Z. G., Gorbachev P.A Raschet kasatel'nogo napryazheniya moroznogo pucheniya vdol' stvola svai pri uchete yeye deformiruyemosti [ Calculation of the tangential stress of frost heaving along the pile shaft, taking into account its deformability]/ Z. G. Ter-Martirosyan, P.A Gorbachev //Zhilishchnoye stroitel'stvo. -2011. - № 12.- P. 36-39. [in Russian]
10. Sakharov I.I. Resheniye trekhmernoy temperaturno-vlazhnostnoy zadachi promerzaniya i pucheniya na primere maloetazhnogo kirpichnogo zdaniya [Solution of the three-dimensional temperature and humidity problem of freezing and heaving on the example of a low-rise brick building] / I.I. Sakharov, V.N. Paramonov, K.G. Shashkin // ZH. Razvitiye gorodov i geotekhnicheskoye stroitel'stvo. -2011.- Vyp. №2. P. 1-12. [in Russian]
11. Popov V.I. Resheniye zadach teplomassoperenosa pri promerzanii - ottaivanii gornykh porod s uchetom uravneniy fazovogo sostoyaniya porovoy vlagi [Solving problems of heat and mass transfer during freezing and thawing of rocks, taking into account the equation of the phase state of pore moisture.]/V.I. Popov, A.S. Kurilko // GIAB. - Tematicheskoye prilozheniye «Fizika gornykh porod»- 2006.- P. 236-242. [in Russian]
12. Dalmatov B.I. Issledovaniya kasatel'nykh sil pucheniya i vliyaniya ikh na fundamenty sooruzheniy [Studies of tangential heaving forces and their influence on the foundations of structures]/B.I. Dalmatov // AN SSSR: Institut merzlotovedeniya.- 1954.- 29 p. [in Russian]
13. Krauch S., Starfild A. Metody granichnykh elementov v mekhanike tverdogo tela [Methods of boundary elements in solid mechanics]. -M .: Mir.- 1987.-328p. [in Russian]