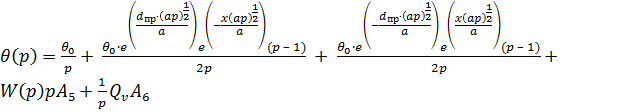ВАРИАНТ РЕШЕНИЯ УРАВНЕНИЙ ТЕПЛО- И ВЛАГООБМЕНА В ЗЕРНОВОМ СЛОЕ ПРИ СВЧ-КОНВЕКТИВНОМ ВОЗДЕЙСТВИИ
Васильев А.Н.1, Будников Д.А.2, Васильев А.А.3
1 ORCID:0000-0002-7988-2338, Доктор технических наук, 2 Кандидат технических наук, 3 Научный сотрудник, Всероссийский научно-исследовательский институт электрификации сельского хозяйства
ВАРИАНТ РЕШЕНИЯ УРАВНЕНИЙ ТЕПЛО- И ВЛАГООБМЕНА В ЗЕРНОВОМ СЛОЕ ПРИ СВЧ-КОНВЕКТИВНОМ ВОЗДЕЙСТВИИ
Аннотация
В предлагаемой статье рассматривается один из вариантов расчета процессов тепло и – влагообмена в слое зерна, когда он продувается агентом сушки и на него действует поле СВЧ. Показано, что при описании процесса дифференциальными уравнениями в частных производных первой степени иногда достаточно выполнить преобразование Лапласа и перейти к численному моделированию с использованием имитационных моделей передаточных функций.
Ключевые слова: зерно, зерновой слой, СВЧ – конвективное воздействие, тепло и – влагообмен, моделирование
Vasilyev A. N.1, Budnikov D.A.2, Vasilyev A.A.3
1 ORCID: 0000-0002-7988-2338, PhD in Engineering, 2 PhD in Engineering, 3 Researcher, All-Russian Federal Research Institute of Electrification of Agriculture
SOLVING EQUATIONS OF HEAT EXCHANGE AND MOISTURE EXCHANGE IN A GRAIN LAYER UNDER MICROWAVE-CONVECTIVE IMPACT
Abstract
Subject of the proposed article is a variant of calculation of heat exchange and moisture exchange in a layer of grain when a flow of drying agent blows through it, and microwave field creates an impact on it. It is shown that if to describe the process as a set of partial differential equations of the first order, it is sometimes enough to perform Laplace transform and proceed with numerical modelling using imitational models of transfer functions.
Keywords: grain, grain layer, microwave-convective impact, heat exchange, moisture exchange, modelling.
Использование полей СВЧ позволяет интенсифицировать конвективную сушку зерна, снизить её энергоёмкость. Моделирование СВЧ – конвективной сушки должно помочь в выявлении её основных параметров и конструкции установок, позволяющих повысить эффективность процесса. Основными элементами математической модели являются дифференциальные уравнения тепло – и влагообмена. Которые требуют своего решения. Дифференциальные уравнения тепло - и влагопереноса при СВЧ обработке записываются как [1, 2]:
где ![]() – коэффициент температуропроводности, м2/с;
– коэффициент температуропроводности, м2/с; ![]() – коэффициент фазового превращения жидкость – пар;
– коэффициент фазового превращения жидкость – пар; ![]() – удельная теплота парообразования, кДж/кг;
– удельная теплота парообразования, кДж/кг; ![]() – удельная мощность, рассеиваемая в диэлектрике при воздействии СВЧ поля, Вт/м3;
– удельная мощность, рассеиваемая в диэлектрике при воздействии СВЧ поля, Вт/м3; ![]() – плотность сухого вещества зерна, кг/м3;
– плотность сухого вещества зерна, кг/м3; ![]() – коэффициент диффузии жидкости, м2/с;
– коэффициент диффузии жидкости, м2/с; ![]() – относительный коэффициент термодиффузии;
– относительный коэффициент термодиффузии; ![]() – избыточное давление в образце, Па;
– избыточное давление в образце, Па; ![]() – емкость тела по отношению к влажному воздуху,
– емкость тела по отношению к влажному воздуху, ![]() ,
, ![]() ;
; ![]() – давление пара материала при данном влагосодержании, Па;
– давление пара материала при данном влагосодержании, Па; ![]() - температура зерна, °С;
- температура зерна, °С; ![]() – коэффициент конвективной диффузии пара, м2/с.
– коэффициент конвективной диффузии пара, м2/с.
При СВЧ – конвективной сушке зерно поочерёдно подвергается воздействию электромагнитного поля, совместно с воздухом, или только агентом сушки. Поле СВЧ воздействует на зерновой слой до того момента, пока его температура не достигнет требуемого предельного значения, например 55оС. После этого магнетроны отключают, и на зерновой слой действует только агент сушки. В это время происходит вынос влаги с поверхности зерна. Конвективную сушку принято описывать известной системой уравнений [3,4]:
где T- температура агента сушки, °C; D - влагосодержание сушильного агента, г/кг; ![]() – текущая влажность зерна, %; V - скорость агента сушки, м/с;
– текущая влажность зерна, %; V - скорость агента сушки, м/с; ![]() ,
, ![]() - теплоемкость воздуха и зерна, кДж/кг·°С;
- теплоемкость воздуха и зерна, кДж/кг·°С; ![]() - порозность зернового слоя;
- порозность зернового слоя; ![]() - удельная поверхность семян, 1/м;
- удельная поверхность семян, 1/м; ![]() - коэффициент теплоотдачи, ккал/кг· ч·°C;
- коэффициент теплоотдачи, ккал/кг· ч·°C; ![]() - объемная масса зерна, кг/м3;
- объемная масса зерна, кг/м3; ![]() - удельный вес воздуха, кг/м3; K - коэффициент сушки, 1/ч;
- удельный вес воздуха, кг/м3; K - коэффициент сушки, 1/ч; ![]() - равновесная влажность зерна, %; х - пространственная координата, м;
- равновесная влажность зерна, %; х - пространственная координата, м; ![]() - время, ч.
- время, ч.
При СВЧ – конвективной сушке изменение температуры зерна происходит за счёт действия поля СВЧ, а тепло – и влагообмен между агентом сушки и зерном – за счёт конвективного обмена. В моменты, когда действие поля СВЧ прекращается тепло и - влагообмен осуществляется за счёт конвективного обмена. Поэтому целесообразно добавить к системе уравнений (4…7) уравнение (1) и использовать полученную систему для расчёта процесса тепло и влагообмена в зерновом слое.
Процессы тепло и – влагообмена в реальных установках отличаются существенной неравномерностью, за счёт конструктивных особенностей устройств, влияющих на глубину проникновения микроволнового поля и распределение агента сушки. Существенное значение имеет зависимость глубины проникновения поля в зерновой слой от его влажности. Поэтому необходимо при разработке модели иметь возможность варьировать значениями скорости воздуха и величинами удельной мощности поля СВЧ в требуемых точках зернового слоя. Для этого целесообразно представить в виде набора элементарных слоёв зерна плотный зерновой слой.
Элементарным будем считать слой в одно зерно. Это позволит для описания процесса использовать максимально возможное количество элементарных слоёв и при необходимости учитывать процессы тепло – и влагообмена непосредственно внутри единичного зерна. С учётом такого допущения в уравнениях (1) и (4…7), пространственная координата х может быть заменена радиусом R зерновки, или её приведённым диаметром dпр.
При разработке математической модели использован ступенчатый метод расчёта [5], при котором температура и влажность агента сушки, прошедшего через элементарный слой становятся температурой и влажностью воздуха, поступающего к следующему элементарному слою. Дополним систему (1) и (4…7) необходимыми уравнениями:
По параметрам агента сушки на входе зернового слоя рассчитывают его равновесную влажность Wp. (8). С учётом данного параметра определяют коэффициент сушки К (9). Далее рассчитывают влажность зерна W (7). Потом, температуру агента сушки Т, которую он приобретает при следовании через единичный слоя зерна (5). Затем рассчитывают температуру зерна ![]() . При СВЧ нагреве используют уравнение (1), а при отключении поля – уравнение (5). После этого определяют влагосодержание D (6) и относительную влажность на выходе из зернового слоя агента сушки (10).
. При СВЧ нагреве используют уравнение (1), а при отключении поля – уравнение (5). После этого определяют влагосодержание D (6) и относительную влажность на выходе из зернового слоя агента сушки (10).
Последовательное выполнение расчетов для каждого элементарного слоя позволит иметь полную картину динамики сушки зерна. Задачи моделирования предусматривают изменение в процессе сушки скорости V воздуха и удельная мощности ![]() поля СВЧ. Это позволит достаточно точно выполнять расчет сушки зерна в установках, при различных алгоритмах управления процессом.
поля СВЧ. Это позволит достаточно точно выполнять расчет сушки зерна в установках, при различных алгоритмах управления процессом.
Прикладное программное обеспечение позволяет построить необходимую имитационную модель. Для построения такой модели элементарного слоя преобразуем дифференциальные уравнения (1), (4…7) в передаточные функции. Для уравнения (7) воспользуемся правилом замены [6] ![]() и получим
и получим ![]() .
.
Уравнения (1), (4), (5), (6) содержат частные производные. Для промежуточного их решения воспользуемся методом интегрального преобразования Лапласа. В этом случае преобразование частных производных осуществляется по следующему правилу [7]:
Если ![]() и преобразование Лапласа производится по переменной
и преобразование Лапласа производится по переменной ![]() , то обозначив
, то обозначив ![]() , можно интегрированием по частям установить соотношение:
, можно интегрированием по частям установить соотношение:
где ![]() – начальное значение температуры.
– начальное значение температуры.
Выполним преобразование Лапласа по ![]() для (4). Для производных температуры зерна
для (4). Для производных температуры зерна ![]() и влажности зерна
и влажности зерна ![]() начальные условия учитывать не будем:
начальные условия учитывать не будем:
Записав уравнение относительно частной производной и заменив координату x на приведённый диаметр зерновки ![]() получим следующее выражение:
получим следующее выражение:
Используя принцип суперпозиции запишем дифференциальное уравнение только с переменной T: ![]() .
.
При этом р играет роль переменной. Решим дифференциальное уравнение относительно ![]() , записав в качестве граничного условия
, записав в качестве граничного условия ![]() .
.
Решение уравнения с использованием пакета MATLAB [8] дало следующий результат:
где ![]() - время задержки при скорости воздуха V в одном зерновом слое.
- время задержки при скорости воздуха V в одном зерновом слое.
Подставив в (12) слагаемые температуры и влажности зерна, получим в операторной форме зависимость изображения температуры теплоносителя T(р) на выходе элементарного слоя от изображений температуры агента сушки Т0(р) на входе в зерновой слой, от изображения текущей температуры зерна ![]() (р), от изображения текущей влажности зерна
(р), от изображения текущей влажности зерна ![]() :
:
По классической схеме, чтобы получить уравнение описывающее зависимость ![]() необходимо выполнить обратное преобразование Лапласа уравнения (13). Попробуем упростить процедуру, представив данную зависимость в виде передаточных функций.
необходимо выполнить обратное преобразование Лапласа уравнения (13). Попробуем упростить процедуру, представив данную зависимость в виде передаточных функций.
Аналогичную процедуру выполним для уравнения (3) и (4). Из уравнения (3) найдём зависимость для изменения температуры зерна элементарного слоя ![]() при конвективной сушке, а из уравнения (4) зависимость для влагосодержания агента сушки на выходе его из зернового слоя
при конвективной сушке, а из уравнения (4) зависимость для влагосодержания агента сушки на выходе его из зернового слоя ![]() . Представив
. Представив ![]() и выполнив преобразование Лапласа для (4) получим следующую зависимость:
и выполнив преобразование Лапласа для (4) получим следующую зависимость:
Для получения зависимости изменения температуры зерна при воздействии электромагнитным полем преобразуем уравнение (1).
Полное уравнение зависимости температуры зерна от его влажности и удельной мощности СВЧ излучения будет иметь следующий вид:
Если достаточно контролировать температуру поверхности зерна, то в этом случае ![]() и уравнение (15) значительно упрощается:
и уравнение (15) значительно упрощается:
В результате проведенных преобразований получен набор уравнений и передаточных функций, с использованием которых осуществляется расчет тепло - и влагообмена в элементарном слое зерна. Запишем его ещё раз:
С использованием полученной системы может быть разработана система компьютерного имитационного моделирования и найдено численное решение уравнений с получением значений параметров зерна и агента сушки.
Литература
- Лыков А.В. Теория сушки – Москва: Энергия, 1968. – 472 с.
- Лыков А.В., Михайлов Ю.А. Теория тепло и массопереноса – Ленинград; Москва: Госэнергноиздат, 1963. – 535 с.
- Анискин В.И., В.А. Рыбарук Теория к технология сушки и временной консервации зерна активным вентилированием - М.: Колос, 1972. - 200 с.
- Васильев А.Н., Руденко Н.Б. Построение математической модели процесса сушки зерна в плотном слое // Современные проблемы использования электрооборудования в сельском хозяйстве (Межвузовский сборник научных трудов. Выпуск 2) - Зерноград, ФГОУ ВПО АЧГАА, 2003. – С. 63-73
- Демин А.В. Методические рекомендации по математическому моделированию процесса сушки и охлаждения зерна в установках плотного слоя - М.: ВИЭCX, - 42 с.
- Бугров Я.С., Никольский С.М. Высшая математика. Дифференциальные уравнеия. Кратные интегралы. Функции комплексного переменного: Учебник для вузов. – 4-е изд. – Ростов н/Д: «Феникс», 1988. -512 с.
- Мартинсон Л.К., Малов Ю.И. Дифференциальные уравнения математической физики: учебник для вузов под ред. В.С. Зарубина, А.П. Крищенко. – Изд. 4-е, стер. - М.: Изд-во МГТУ им. Н.Э. Баумана, 2011. – 367 с.
- Ануфриев И.Е., Смирнов А.Б., Смирнова Е.Н. MATLAB – СПб.: БХВ-Петербург, 2005. – 1104 с.
References
- Lykov A.V. Teorija sushki – Moskva: Jenergija, 1968. – 472 s.
- Lykov A.V., Mihajlov Ju.A. Teorija teplo i massoperenosa – Lenin-grad; Moskva: Gosjenergnoizdat, 1963. – 535 s.
- Aniskin V.I., V.A. Rybaruk Teorija k tehnologija sushki i vremennoj konservacii zerna aktivnym ventilirovaniem - M.: Kolos, 1972. - 200 s.
- Vasil'ev A.N., Rudenko N.B. Postroenie matematicheskoj modeli processa sushki zerna v plotnom sloe // Sovremennye problemy ispol'zovanija jelektrooborudovanija v sel'skom hozjajstve (Mezhvuzovskij sbornik nauchnyh tru-dov. Vypusk 2) - Zernograd, FGOU VPO AChGAA, 2003. – S. 63-73
- Demin A.V. Metodicheskie rekomendacii po matematicheskomu mode-lirovaniju processa sushki i ohlazhdenija zerna v ustanovkah plotnogo sloja - M.: VIJeCX, 1977. - 42 s.
- Bugrov Ja.S., Nikol'skij S.M. Vysshaja matematika. Differencial'-nye uravneija. Kratnye integraly. Funkcii kompleksnogo peremennogo: Uchebnik dlja vuzov. – 4-e izd. – Rostov n/D: «Feniks», 1988. -512 s.
- Martinson L.K., Malov Ju.I. Differencial'nye uravnenija matema-ticheskoj fiziki: uchebnik dlja vuzov pod red. V.S. Zarubina, A.P. Krishhenko. – Izd. 4-e, ster. - M.: Izd-vo MGTU im. N.Je. Baumana, 2011. – 367 s.
- Anufriev I.E., Smirnov A.B., Smirnova E.N. MATLAB 7. – SPb.: BHV-Peterburg, 2005. – 1104 s.