СПОСОБ РАСПРЕДЕЛЕНИЯ РАБОЧИХ ЧАСТОТ МЕЖДУ РАДИОЭЛЕКТРОННЫМИ СРЕДСТВАМИ НА ОСНОВЕ АНАЛИЗА ПОТЕРЬ ИНФОРМАЦИИ

Теряев Д.В.¹, Лосенков А.А.², Павлов А.Н.²

¹Кандидат технических наук, ВА ВПВО ВС РФ, ² ВА ВПВО ВС РФ

Работа выполнена при поддержке гранта Президента Российской Федерации МК-6544.2014.10

СПОСОБ РАСПРЕДЕЛЕНИЯ РАБОЧИХ ЧАСТОТ МЕЖДУ РАДИОЭЛЕКТРОННЫМИ СРЕДСТВАМИ НА ОСНОВЕ АНАЛИЗА ПОТЕРЬ ИНФОРМАЦИИ

Аннотация

В статье рассмотрено применение генетического алгоритма для решения задач использования частотного ресурса для обеспечения электромагнитной совместимости между радиоэлектронными средствами специального назначения

Ключевые слова: генетический алгоритм, коэффициент значимости, радиоэлектронные средства.

 

Terjaev D.V.¹, Losenkov A.A.², Pavlov A.N.²

¹PhD in Engineering, Military Academy of Army Air Defense AF RF, ² Military Academy of Army Air Defense AF RF

MEANS OF OPERATION FREQUENCY DISTRIDUTION BETWEEN RADIO ELECTRONIC EQUIPMENT BASED ON INFORMATION LOSS ANALYSIS

Abstract

The article deals with the application of genetic algorithm (AG) for solving tasks of frequency resource usage to provide electromagnetic  compatibility between radio electronic equipment special uses.

Keywords: genetic algorithm, relevancy factor, radio electronic equipment.

Основной величиной, характеризующей работу радиоэлектронных средств (РЭС), является рабочая частота. Каждая РЭС имеет свой штатный набор частот, что позволяет проводить отстройку от помех. Здесь можно говорить о потери информации, в результате воздействия непреднамеренных помех при определенном сочетании приемных и передающих частот.

При рассмотрении методов, позволяющих решить поставленную задачу распределения частот, наибольший научный интерес представляет использование генетического алгоритма. Реализация метода генетического алгоритма позволяет находить не только глобальный, но и локальные минимумы функции весовых значений сочетаний рабочих частот, что дает возможность найти несколько рациональных решений, причем относительно быстро.

При использовании этого алгоритма для распределении частот РЭС в качестве элементов хромосом выступают рабочие частоты.

Состав хромосомы представляет собой набор РЭС, функционирующих в реальном масштабе времени своего применения с определенными рабочими частотами. Каждая рабочая частота, характеризуется потерями информации (наложенными на нее ограничениями). Сумма потерь информации РЭС (рабочих частот), участвующих в процессе применения в реальном масштабе времени, позволяет определить приспособленность хромосомы.

Однако, в современных условиях простое арифметическое сложение потерь информации не позволит в достаточной мере оценить качество выполнения специальной задачи. Чтобы рационально решить задачу по распределению рабочих частот РЭС управляемой структуры используются весовые коэффициенты, позволяющие определить степень вклада каждой используемой РЭС в решение поставленной задачи. При этом все весовые коэффициенты определяются статистическим методом.

Математический аппарат распределения рабочих частот РЭС в сложной электромагнитной обстановке (ЭМО) напрямую зависит от порядка определения весового коэффициента РЭС, сущность которого сводится к определению коэффициента значимости K_i i - ой РЭС в сложной обстановке в реальном масштабе времени.

Примем:

N - количество РЭС управляемой структуры, функционирующих в сложной обстановке реального масштаба времени;

 – потери информации в приемном тракте i-го РЭС от воздействия НРП;

Потери информации определены в пределах:

(1)

Именно от коэффициента значимости функционирующей в специальной обстановке РЭС зависит качество распределения рабочих частот в управляемой структуре.

Будем считать показателем качества распределения рабочих точек (КР) значение следующей функции:

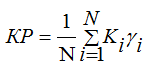(2)

где K_i –коэффициент значимости i - ой РЭС в реализуемом эпизоде;

Коэффициенты значимости определяем в интервале:

(3)

Таким образом качество распределения рабочих точек РЭС определяется в пределах:

(4)

Графиком зависимости коэффициентов значимости K_i будет являться зависимость вида K_i =1/N. График зависимости

Используя в качестве n текущее значение номера приоритета РЭС, используемого в выполняемом эпизоде (от 1 до N).

Например, проведя расчеты значений коэффициентов значимости, для случая выполнения эпизода десятью РЭС получим значения, сведенные в таблицу 1.

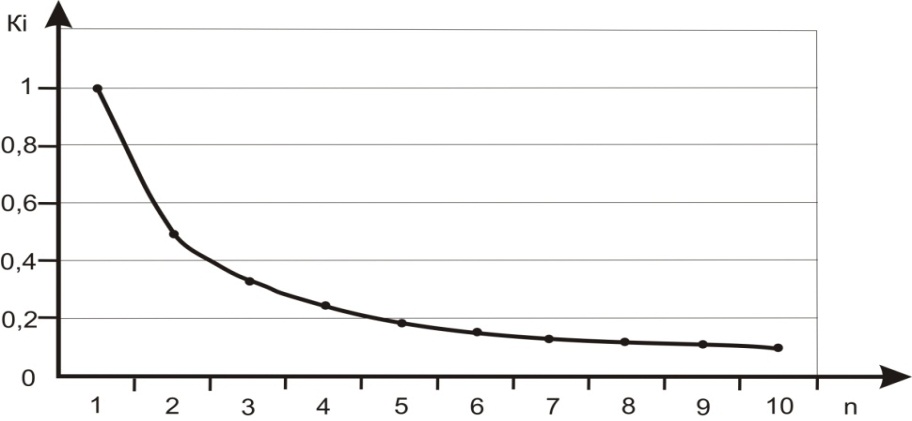
Графиком зависимости коэффициентов значимости К_i будет являться зависимость вида K_i=1/n (рисунок 1).

Рисунок 1 - Зависимость значений коэффициентов значимости K_i  от номера n (приоритетность РЭС)

Рассмотренный вариант не учитывает ряд других факторов, таких как подготовку операторов РЭС, качество настройки аппаратуры и др. В связи с этим, для получения более точных значений качества распределения рабочих точек используют поправочные коэффициенты:

 

(5)

где К_{попр i} – поправочный коэффициент i – го РЭС, участвующего в выполнении задачи;

При использовании статистического метода можно говорить о следующей зависимости:

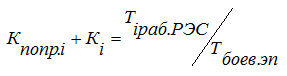(6)

где T_{i раб РЭС} – время использования информации от i - ой РЭС, участвующей в выполнении эпизода;

T_{боев. эп.} – время выполнения эпизода.

Для определения поправочного коэффициента статистическим методом, необходимо использование достаточно большое количество вариантов (не менее 10), выполнения конкретных задач с постоянным набором РЭС.

Критериями оценки весового коэффициента являются:

степень важности РЭС;

количество рабочих частот, на которые возможна перестройка РЭС;

время перехода с одной рабочей частоты на другую.

Также возможны и другие дополнительные критерии, на основании которых определяется весовой коэффициент.

Сумма всех потерь информации, умноженная на соответствующие весовые коэффициенты, и определит приспособленность данной хромосомы.

Набор хромосом с различными сочетаниями рабочих частот, используемых в РЭС, формирует популяцию.

Применяя стандартные функции генетического алгоритма и вводя критерий останова (например: достижения определенной приспособленности хромосомой или минимума приспособленности), определяем набор из хромосом, являющихся решением поставленной задачи.

Критерием для останова в нашем случае будет выступать попадание оценки приспособленности нашего набора (хромосомы) в область, достаточную для качественного выполнения поставленной задачи (критерий снижения качества функционирования).

Для практического применения алгоритма важное значение имеют такие свойства как сходимость, способность к отысканию всего множества рациональных решений, быстродействие. С этой целью было проведено тестирование алгоритма в различных условиях обстановки.

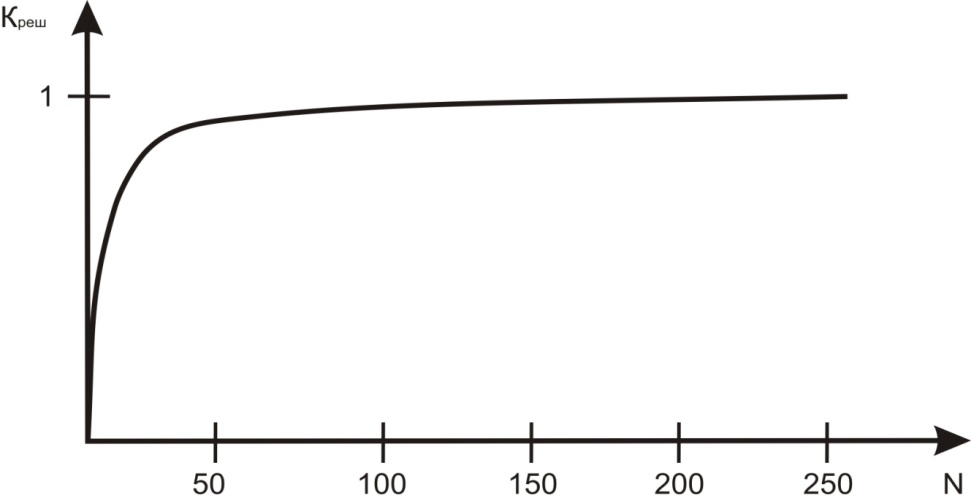
Оценка сходимости алгоритма (рисунок 2) показала, что он достаточно быстро находит экстремум функции.

Рисунок 2 – Зависимость рассчитанной степени нахождения рациональных решений от количества итераций генетического алгоритма

Под К_реш  понимается найденное количество  решений по отношению к общему количеству имеющихся рациональных решений.

Под N понимается количество итераций генетического алгоритма.

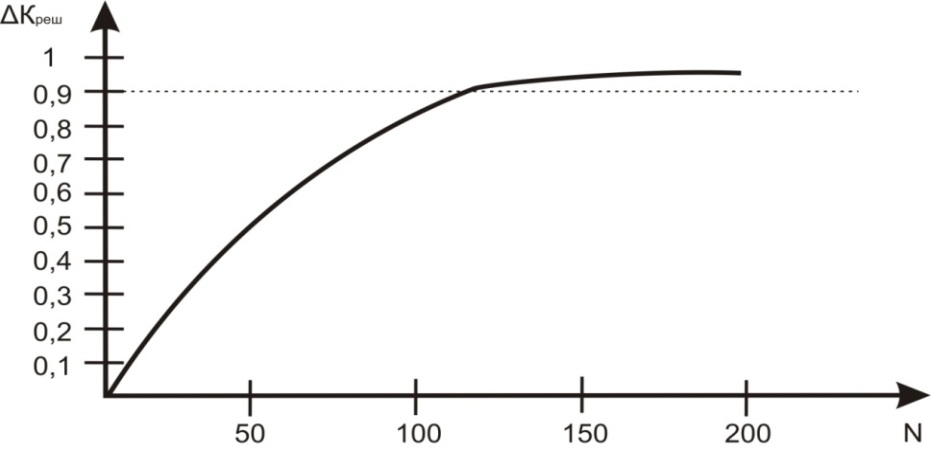
Результат оценки возможности отыскания всех экстремумов (рисунок 3) показывают, что алгоритм способен найти не менее 90% рациональных вариантов, но для этого требуется достаточно большое число итераций от 50 до 100.

Рисунок 3 – Зависимость доли найденных рациональных вариантов решений от количества итераций генетического алгоритма

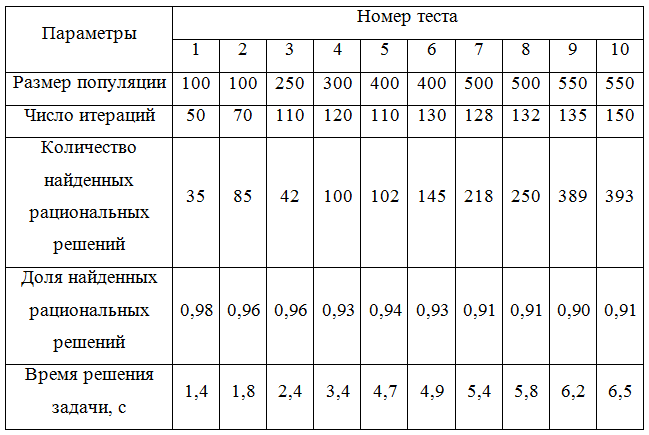
Сводные результаты тестирования алгоритма в различных условиях приведены в таблице 1.

Анализ данных приведенных в таблице, показывает, что алгоритм способен находить 90-98% рациональных вариантов решения. Время поиска зависит от размера популяции, числа итераций, характера исследуемой области и может составлять от 1,4 до 6,5с.

Результаты тестирования показывают, что предлагаемый алгоритм может быть использован в системе реального времени.

Принцип работы генетического алгоритма заключается в следующей схеме:

1. Создание начальной популяции из n хромосом.
2. Вычисление для каждой хромосомы её пригодность.
3. Выбираем пару хромосом – родителей с помощью перебора.
4. Проводим кроссинговер двух родителей, производя двух потомков.

Таблица 1 - Сводная таблица результатов тестирования алгоритма

5. Проводим мутацию потомков.
6. Повторяем шаги 3-5, пока не будет сгенерировано новое поколение популяции, содержащее n хромосом.
7. Повторяем шаги 2-6, пока не будет достигнут критерий окончания процесса.

В статье рассмотрен способ распределения рабочих частот между РЭС на основе метода генетического алгоритма.

Предложенный способ распределения рабочих частот между РЭС позволяет быстро находить приемлемое решение в поставленной специальной задаче.

Благодаря использованию генетического алгоритма на выходе мы получим несколько решений близких к оптимальному, они будут являться дополнениями к основному, определяемому вводимым критерием предпочтения (количество перестроек по частоте РЭС относительно изначального значения).

Литература

1. Борисов В. В., Круглов В. В., Харитонов Е. В. Основы построения нейронных сетей. – Смоленск: Изд-во Военного ун-та войсковой ПВО ВС РФ, 1999. 348 с.
2. Босс В. Лекции по математике  / Перебор и эффективные алгоритмы // М.: ЛКИ, 2008. – Т.10.
3. Новиков И.И., Соловьев В.В. Универсальный алгоритм оптимального присвоения частот. // Радиотехника. - М.: 2002. №10. с. 105-108.
4. Панченко Т.В. Генетические алгоритмы. / Астраханский университет, 2007. 88 c.
5. Соловьев В.В., Харченко Т.В. Комплексное применение алгоритмов комбинаторной, игровой и поисковой оптимизации в задачах присвоения частот. // Радиотехника - М.: 2005. №9. с. 109-106.

References

1. Borisov V. V., Kruglov V. V., Haritonov E. V. Osnovy postroenija nejronnyh setej. – Smolensk: Izd-vo Voennogo un-ta vojskovoj PVO VS RF, 1999. 348 s.
2. Boss V. Lekcii po matematike / Perebor i jeffektivnye algoritmy // M.: LKI, 2008. – T.10.
3. Novikov I.I., Solov'ev V.V. Universal'nyj algoritm optimal'nogo prisvoenija chastot. // Radiotehnika. - M.: 2002. №10. s. 105-108.
4. Panchenko T.V. Geneticheskie algoritmy. / Astrahanskij universitet, 2007. 88 c.
5. Solov'ev V.V., Harchenko T.V. Kompleksnoe primenenie algoritmov kombinatornoj, igrovoj i poiskovoj optimizacii v zadachah prisvoenija chastot. // Radiotehnika - M.: 2005. №9. s. 109-106.