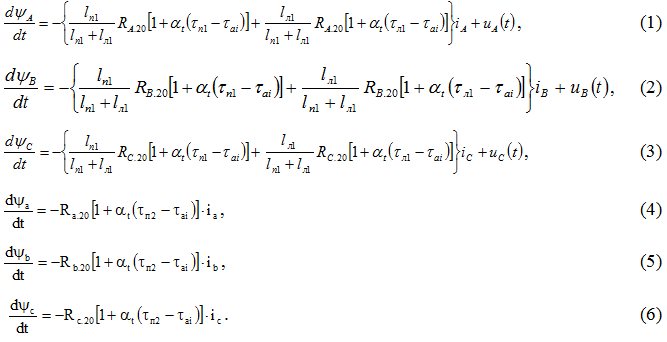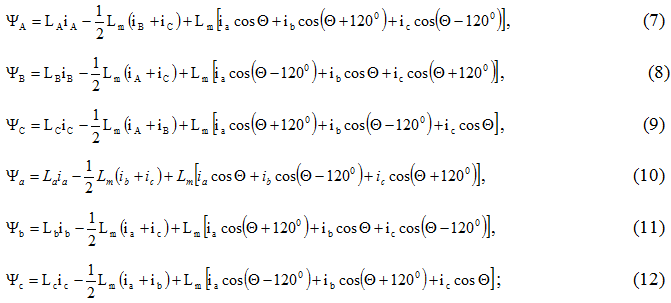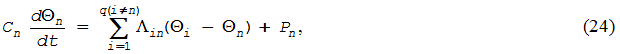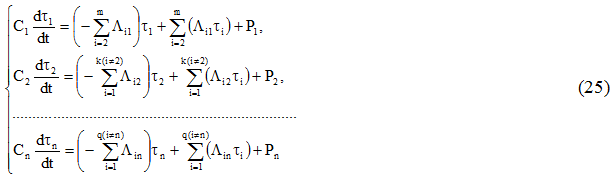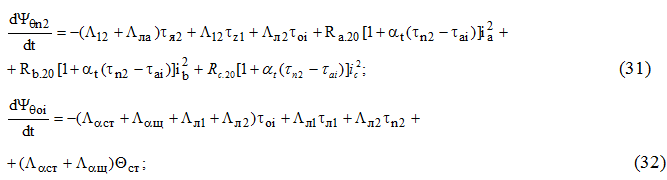МОДЕЛИРОВАНИЕ ДИНАМИЧЕСКИХ РЕЖИМОВ РАБОТЫ АСИНХРОННОЙ МАШИНЫ С УЧЕТОМ ТЕПЛОВЫХ ПЕРЕХОДНЫХ ПРОЦЕССОВ
Архипова О.В.1, Ковалев В.З.2, Ковалева С.Е.3
1ORCID: 0000-0002-8773-8846, Югорский государственный университет, 2ORCID: 0000-0002-4512-6868, Доктор технических наук, профессор, Югорский государственный университет, 3 АУ «Ханты-Мансийский технолого-педагогический колледж»
Статья выполнена в рамках проекта №1681 государственного задания в сфере научной деятельности
МОДЕЛИРОВАНИЕ ДИНАМИЧЕСКИХ РЕЖИМОВ РАБОТЫ АСИНХРОННОЙ МАШИНЫ С УЧЕТОМ ТЕПЛОВЫХ ПЕРЕХОДНЫХ ПРОЦЕССОВ
Аннотация
Динамические процессы в асинхронной машине протекают с изменением температуры ее отдельных частей. В свою очередь это приводит к изменению омического сопротивления обмоток и как следствие, к изменению энергетических характеристик всей машины.
Возникает задача анализа асинхронной машины с учетом тепловых переходных процессов.
Математическая модель электромагнитной, механической и тепловой подсистем, в соответствии с энергетическим подходом к моделированию электротехнических комплексов и систем, построена в канонической форме.
При выводе уравнений переходного процесса асинхронной машины, с учетом тепловых процессов, сделаны допущения о ненасыщенности пути основного магнитного потока, отсутствии демпфирующих контуров.
Ключевые слова: моделирование, асинхронная машина, переходные процессы, тепловые процессы, математическое моделирование.
Arkhipova O.V.1, Kovalev V.Z.2, Kovaleva S.E.3
1 ORCID: 0000-0002-8773-8846, Yugra State University, 2 ORCID: 0000-0002-4512-6868, PhD in Engineering, Professor, Yugra State University, 3 Khanty-Mansiysk Technological and Pedagogical College
SIMULATION OF DYNAMIC MODES OF ASYNCHRONOUS MACHINES WITH REGARD TO THERMAL TRANSITION PROCESSES
Abstract
Dynamic processes in the asynchronous machine proceed with the change of the temperature of its particular parts. In its turn it leads to a change in the ohmic resistance of the windings and consequently, to changes in the energy performance of the whole machine.
A task of analysis of asynchronous machines with regard to thermal transition processes arises.
Mathematical model of electromagnetic, mechanical and thermal subsystems, in accordance with the energy approach to the modelling of electrotechnical complexes and systems, built in canonical form.
In deriving the equations of the transition process of asynchronous machine, with regard to thermal processes, assumptions about the unsaturation of the main path of the magnetic flux, the absence of damping circuits are made.
Keywords: simulation, asynchronous machine, thermal processes, transition processes, mathematic simulation.
Dynamic processes in the asynchronous machine proceed with the change of the temperature of its particular parts. In its turn it leads to a change in the ohmic resistance of the windings and consequently, to changes in the energy performance of the whole machine.
A task of analysis of asynchronous machines with regard to thermal transition processes arises.
Mathematical model of electromagnetic, mechanical and thermal subsystems, in accordance with the energy approach to the modelling of electrotechnical complexes and systems, built in canonical form [7].
In deriving the equations of the transition process of asynchronous machine, with regard to thermal processes, assumptions about the unsaturation of the main path of the magnetic flux, the absence of damping circuits are made. After transformations we get the following [4,5,8]:
Herein:
– the flux linkage of the winding
- the active resistance of the phase windings of the stator and rotor are given for an ambient temperature of 200C
- the active resistance of the phase windings of the stator and rotor are given for an ambient temperature of 200C
- the temperature of the induction motor parts
- the phases currents of the stator of an induction motor
– geometrical parameters (length of end-winding and slot winding of strator of induction motor)
We accept hereinafter:
Accounting changes of the resistance of the windings of the stator and rotor in dependence on temperature is based on the method of equivalent thermal circuits which suggests the analogy of heat flow with electric current I based on a single form of the equations of heat exchange (Fourier's law)
and electric current (Ohm's law)
where Sср — the average area of heat transfer surface; λ — thermal conductivity coefficient; ΔΘ — temperature fall on the length δ; Rλ — the thermal resistance of this portion of the path of heat flow; k — specific conductance; ΔU — the potential difference on the length of the conductor l with a cross section S; Rэ — electrical resistance.
The basic assumptions of the heat diagram method are the following [9]:
- The electric machine is represented in the form of a system of homogeneous bodies, relations between which are determined by the type and the conditions of heat exchange.
- The electric machine is divided into "parts" within the dimensions of which the conditions of heating-cooling remain constant. In the plane of symmetry of each body the node is set, the resistance of heat exchange with other bodies is connected to him , and concentrated equivalent thermal resistance substituting the actual distributed, are assumed to be not dependent on the magnitude of heat flow; losses that occur in this part of electric machine are put in the nodes. Thus the actual distributed heat sources are replaced by lumped.
- Heat calculation is reduced to the calculation of the average temperature of all machine components. We believe that heat flow in the longitudinal cross section is absent, it allows to consider a flat task in the cross-section of the machine; individual conductors are equal to the average overtemperature in this section in the cross section of the winding overtemperature; we consider the thermal conductivity coefficient of the materials constant.
Electric machine, including induction motor in thermal relation is always a complex set of interrelated elements, processes in which mathematically by a system of Poisson's equations in partial derivatives are described. Interrelated and и interdependent boundary conditions for these equations sophisticate the solution. The failure to consider the field of temperatures within individual element allows you to provide thermal processes by the system of ordinary linear differential equations of the first order. Their number depends on the number of bodies in which the machine is broken. Thermal state of the n-th body taking into account the above assumptions is described as a differential equation of the heat balance:
where Сn — the heat capacity of n-th body; Θn — the temperature of n-th body; Θi — the temperature of one of the near bodies i; q — the number of bodies connected in a heat relation with the considered body n; Λin — the heat transfer from one of the neighboring bodies i to this body n; Рn — loss of power in this body n; t — the current time.
We have the following for electrical machines, divided into the system of n bodies in thermal relation with the given assumptions 1) -3):
where m — the number of bodies, connected in a heat relation with the first body;
k — the number of bodies, connected in a heat relation with the second body.
From the analysis of the pattern of heat transfer of short-circuited induction motor with a degree of protection IP44, on the assumption that the thermal resistance between the frame and panels is missing; heat transfer through the shaft is negligible; assumptions are adhered 1)–3), and the whole system is symmetric, simplified thermal equivalent circuit can be made (TEC). It consists of seven bodies: the stator teeth with an average temperature of τzl; strator with an average temperature of τal; a shell comprising a frame and end shields, with an average temperature of ; slot winding of the stator with an average temperature of τnl; end-winding of the stator with an average temperature of τπl; winding and the rotor teeth with an average temperature of τn2; inner air with an average temperature of τoi.
Body of TEC are linked by respective thermal conductivities. Sources of heat concentrated at the appropriate nodes are: basic and additional losses in the stator teeth 
; losses in the stator yoke 
, copper losses of the slot part of the winding ; copper losses of end-winding of the stator Рм1л=Pм1lл1/(l1+lл1); losses in the rotor, including the electrical losses in a short-circuited squirrel cage Рм2 and additional losses in teeth Рcz2; inner mechanical losses, consisting of friction losses in the bearings and friction losses of the rotor against the air 
(we will keep them in the shell).
Based on the previously made assumptions, the received split of asynchronous motor into parts with equal temperatures and taking into account equations (24) we have the following:
Subsystem of algebraic equations:
Herein 
– heat conductivity; 
– total specific heats.
Problem-oriented numerical methods [7,9] applicable directly to these equations are required for solutions of the built system of equations of the dynamics of induction motor taking into account the thermal processes (26) - (39).
Resume:
- The dynamic model of asynchronous machines with regard to thermal transition processes has been worked out. The structure of the model – is a mixed system of fluxional and algebraic equations.
- The necessity of creation of special numerical method for solution of the built mixed system of fluxional and algebraic equations has been shown.
References
- Kovalev, V.Z. Process control simulation of electrotechnical complexes and systems // Control systems and information technologies. Publishing House Science Book, limited. Voronezh. № 1.2 (35). p.p. 259-263. [in Russian].
- Kovalev V.Z., Scherbakov A.G. Informational System for Identification of Parameters of Mathematical Model of Electrotechnical Complexes // Control systems and information technologies. Publishing House Science Book, limited. Voronezh. № 1 (35). p.p. 57-59. [in Russian].
- Kovalev V.Z., Malgin G.V., Arkhipovа O.V. Mathematical modeling of electrotechnical oil production complexes, for energy-saving aims: monograph // Department of Education and Science KHMAO-Yugra, Yugra State University. Khanty-Mansiysk. 2008.p. 222. [in Russian].
- Kovalev V.Z., Scherbakov A.G., Kovalev A. Yu. Identification of parameters and characteristics of Electrotechnical devices Mathematical Models: monograph // Fed. Educational agency. Omsk State Technical Univ. 2005. p.121 [in Russian].
- Kovalev V.Z. Modeling of electrotechnical complexes and systems, as summation of interacting subsystems with different physical nature// Doctoral dissertation. Omsk. 2000. p.261 [in Russian].