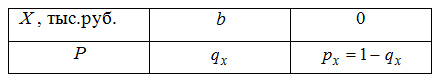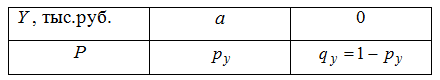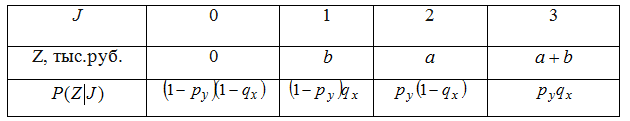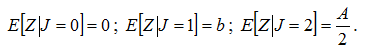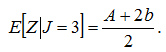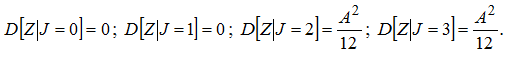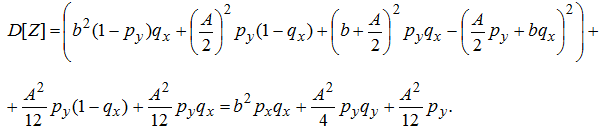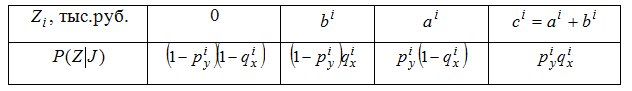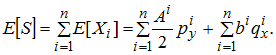ОБ ОДНОЙ ЗАДАЧЕ АКТУАРНОЙ МАТЕМАТИКИ

Микишанина Е.А.¹, Михайлова А.А.²

¹старший преподаватель, ²студент, Чувашский государственный университет имени И.Н. Ульянова

ОБ ОДНОЙ ЗАДАЧЕ АКТУАРНОЙ МАТЕМАТИКИ

Аннотация

В работе производится расчет убытков страховой компании по пакету страхования, состоящего из двух договоров, а также расчет суммарного убытка по всем застрахованным. Рассмотрены простейшие одногодичные контракты обязательного страхования автогражданской ответственности и добровольного страхования жизни.

Ключевые слова: договор страхования, убытки, портфель договоров.

Mikishanina E.A.¹, Mikhailova A.А.²

¹senior lecturer, ²student, Chuvash State University named after I.N. Ulyanov

ON THE PROBLEM OF ACTUARIAL MATHEMATICS

Abstract

In the work calculation of losses of the insurance company for the insurance package consisting of two agreements is made, as well as the calculation of the total loss for all insured is made. Simple one-year contracts of compulsory motor third party liability insurance and voluntary life insurance are considered.

Keywords: insurance contract, material losses, portfolio of contracts.

Кризис страхования обязательной автогражданской ответственности привел к тому, что в  последнее время в страховых компаниях стало очень актуальным «портфельное» страхование,  когда совместно с договором обязательного страхования заключается договор добровольного страхования. Например, ОСАГО (обязательное страхование автогражданской ответственности) и КАСКО (добровольное страхование автотранспортного средства) или ОСАГО и НС (страхование жизни от несчастного случая).

Рассмотрим пакет краткосрочных договоров страхования ОСАГО и НС и рассчитаем убытки страховой компании по этому портфелю.

На данный момент лимиты ответственности по полису ОСАГО одинаковы на всей территории РФ и для всех полисов ОСАГО. Лимит по страхованию жизни страхователь устанавливает сам, но, как правило, эта сумма также ограничена снизу самой страховой компанией.

К настоящему времени в условиях жесткой конкуренции на рынке страхования рентабельность страховых операций продолжает снижаться, поэтому анализ убытков страховой компании позволяет наиболее достоверно определить резервный фонд и риски страховой  компании, связанные с резервирование убытков.

Рассмотрим простейшие одногодичные контракты обязательного страхования автогражданской ответственности и страхования жизни.

Постановка задачи.  Автовладелец  Н. купил страховой полис ОСАГО и дополнительно заключил договор страхования жизни (НС) на следующих условиях.

По договору страхования жизни страховщик выплачивает сумму  в случае смерти или получения застрахованным инвалидности I группы. В противном случае убытки страховой компании равны нулю.  Таким образом, имеем закон распределения величины убытков страховой компании X по данному виду договора

q_x – вероятность смерти застрахованного в течение года (значения берутся из таблицы смертности населения);

b - величина страхового возмещения.

По договору ОСАГО величина убытка страховой компании имеет следующее распределение:

a – величина выплаты по полису ОСАГО,  является равномерно распределенной случайной величиной в интервале (0, A), где A - лимит ответственности по данному виду договора;

p_y – вероятность наступления страхового случая (ДТП).

Определим среднее значение и вариацию убытка страховой компании.

Решение. Для страховой компании существует четыре возможных варианта произведения выплат. Введем индикатор события «был страховой случай» J , который будет иметь следующие возможные значения:

Введем новую случайную величину Z, характеризующую величину убытка по описанному портфелю страхования. Будем считать, что случайные величины X,Y - независимы. Тогда закон распределения вероятностей случайной величины  Z  будет иметь вид:

Для определения среднего значения убытка страховой компании воспользуемся формулой для вычисления математического ожидания:

Вычислим условные математические ожидания.

В случае J=3 величина убытка Z=a+b является случайной и равномерно распределенной в интервале (b, b+A), поэтому

Математическое ожидание случайной величины Z имеет вид

Для определения значения вариации убытка страховой компании воспользуемся формулой для вычисления дисперсии:

Вычислим условные дисперсии:

Тогда

Для страховой компании интерес представляет не конкретная страховая выплата, а общая сумма выплат всем застрахованным. Пусть S = Z₁ + ... + Z_n - суммарная величина убытка, n - общее число застрахованных, Z_i - размер индивидуального ущерба по i-му портфелю, состоящему из двух договоров ОСАГО и НС, описанных выше.

Будем считать  независимыми и имеющими распределение

Здесь  aⁱ  - величина выплаты по i-му полису ОСАГО, равномерно распределенная случайная величина в интервале (0, Aⁱ), bⁱ - детерминированная величина выплаты по i-му договору НС, pⁱ_y, qⁱ_x - соответствующие вероятности событий для каждого застрахованного, зависящие от возраста региона и т.п.   Тогда суммарный размер ожидаемого убытка страховой компании будет равен

Размер премий  по договорам страхования устанавливаются исходя из условия неотрицательности потерь страховой компании, т.е.

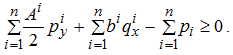
Литература

1. Алексеев Б.В., Егорова Д.В., Иваницкий А.Ю. Введение в финансовую и актуарную математику: Учебное пособие. - Чебоксары : Изд-во Чуваш. ун-та, 2001. - 322 с.

References

1. Alekseev B.V., Egorova D.V., Ivanickij A.Ju. Introduction to actuarial and financial math. [Alekseev B.V., Egorova D.V., Ivanickij A.Ju.  Vvedenie v finansovuju i aktuarnuju matematiku: Uchebnoe posobie]. Cheboksary,  Izd-vo Chuvash. un-ta, 2001, 322 р.