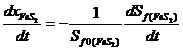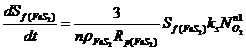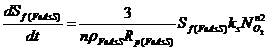МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССА АВТОКЛАВНОГО ОКИСЛЕНИЯ ПИРИТ-АРСЕНОПИРИТ СОДЕРЖАЩЕГО КОНЦЕНТРАТА

Карастелев Н. А.¹, Шариков Ю.В.²

¹ Аспирант, Национальный минерально-сырьевой университет «Горный», ² Доктор технических наук, профессор, Национальный минерально-сырьевой университет «Горный»

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССА АВТОКЛАВНОГО ОКИСЛЕНИЯ ПИРИТ-АРСЕНОПИРИТ СОДЕРЖАЩЕГО КОНЦЕНТРАТА

Аннотация

В статье рассмотрена математическая модель автоклавного окислительного процесса применительно к переработке сульфидного золотосодержащего концентрата. Проведена параметрическая идентификация неизвестных параметров модели на основе поставленных кинетических опытов. Получены результаты моделирования, а также оценка адекватности предложенной математической модели.

Ключевые слова: пирит, арсенопирит, упорное золото, автоклавный окислительный процесс, математическое моделирование.

Karastelev N.A.¹, Sharikov I.V.²

¹ Postgraduate Student, National Mineral Resources University (University of Mines), ² PhD in Engineering, Professor, National Mineral Resources University (Mining University)

MATHEMATICAL MODELING OF THE PRESSURE OXIDATION OF SULPHIDE CONCENTRATES

Abstract

The article considers the mathematical model of autoclave oxidation process as applied to treatment of gold-bearing sulphide concentrates. The parametric identification of unknown model parameters was performed by using the set of kinetic experiments. The results of modeling and assessment of adequacy of mathematical model were presented. 

Keywords: pyrite, arsenopyrite, refractory gold, pressure oxidation process, mathematical simulation.

1. Вступление

Автоклавный окислительный процесс, как способ разрушения и растворения содержащихся в материале пирита (FeS₂) и арсенопирита (FeAsS) с целью вскрытия поверхности ассоциированных с данными минералами частиц тонкодисперсного золота, получил широкое признание и распространение в золотодобывающей промышленности. В основу процесса положено окисление содержащихся в концентрате сульфидных минералов под действием кислорода в аппаратах способных поддерживать высокие температуру (220–230 °С) и давление (3,5–3,7 МПа), согласно следующим химических реакциям:

2FeS₂ + 7O₂ + 2H₂O →2FeSO₄ + 2H₂SO₄,                                     (1)

4FeAsS + 13O₂ + 6H₂O → 4FeSO₄ + 4H₃AsO₄.                            (2)

Образующийся по реакциям (1-2) сульфат железа (II) окисляется кислородом до сульфата железа (III):

4FeSO₄ + O₂ + 2H₂SO₄ → 2Fe₂(SO₄)₃ + 2H₂O.                     (3)

Автоклавное окисление сульфидов происходит в процессе взаимодействии твердой, жидкой и газообразной фаз: диспергированный в жидкой фазе кислород за счет массообменных процессов вступает в реакцию с твёрдыми частицами сульфидов. Скорость протекания различных стадий окислительного процесса характерна для различных по составу концентратов, а также условий в которых протекает окисление: температура процесса, парциальное давление кислорода, крупность материала, время пребывание материала и т. д. С целью оценки влияния данных факторов на основной показатель окислительного процесса – степень разложения сульфидных материалов, как правило, исследуется кинетика автоклавного окисления конкретного концентрата. Полученные в ходе проведенных экспериментов результаты обобщаются с помощью адекватной математической модели процесса, необходимой как для оптимизации, так и для масштабирования результатов на реальный промышленный процесс. С этой целью проведён ряд кинетических опытов, анализ и разработка математического описания автоклавного процесса, а также моделирование и оценка адекватности полученной модели.

2. Экспериментальная часть

Методика проведения кинетического эксперимента. Автоклавное окисление пирит-арсенопирит содержащего материла проводили в титановом автоклаве фирмы Buchi Glass Uster (Швейцария) объемом 1,1 дм³ (рабочий объем 0,680 дм³), снабженном системой автоматического поддержания температуры в реакторе и турбинной мешалкой диаметром 60 мм с регулируемым числом оборотов. Кислород подается непосредственно под мешалку по заглубленной титановой трубке.

Из навески концентрата готовили пульпу с заданным отношением Ж:Т и переносили её в автоклав. Автоклав герметизировали и продували кислородом, затем начинался разогрев автоклава до рабочей температуры при включенной мешалке. По достижению рабочей в автоклав подавали кислород, задавали рабочее число оборотов мешалки и фиксировали начало автоклавного опыта. В течении опыта непрерывно поддерживали заданную температуру процесса с точностью ±1°, компенсируя излишки выделяющегося тепла охлаждением через заведенный в автоклав змеевик. Заданное парциальное давление кислорода автоматически поддерживалось регулятором давления фирмы Bronkhorst (Голландия), а мгновенный расход кислорода непрерывно фиксировался установленным на кислородной линии расходомером с интервалом менее одной секунды. Получаемые в реальном времени мгновенный и суммарный расход кислорода позволяют судить о скорости и степени завершенности процесса окисления. При прекращении расхода кислорода в автоклав подача кислорода перекрывалась, автоклав охлаждался с последующим сбросом давления до атмосферного и выгрузкой окисленной пульпы.

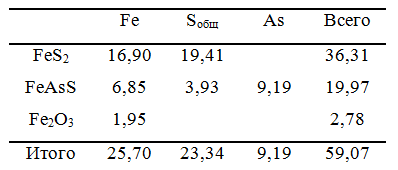
Исследуемый материал и проведенная серия опытов. С целью проведения параметрической идентификации предложенной модели автоклавного окисления проведена серия кинетических опытов, приведенная в таблице 2. В качестве исследуемого материала использован золотосодержащий концентрат (содержание золота порядка 23,8 г/т), упорность которого обусловлена присутствием пирита (порядка 36% по массе) и арсенопирита (порядка 20% по массе). Химический и минералогический состав исследуемого материала приведены в таблице 1.

.

 Таблица 1 – Химический и минералогический состав исследуемого пирит-арсенопирит содержащего концентрата

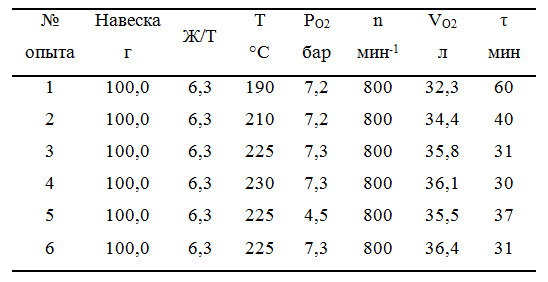
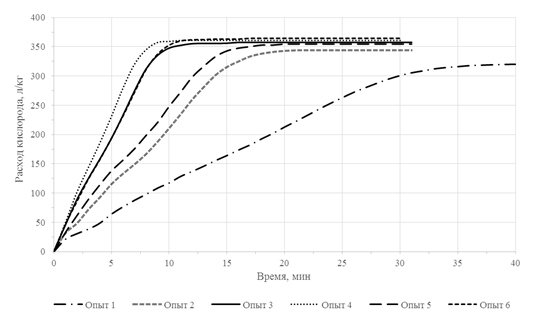
В ходе проведения серии экспериментов варьировали температуру процесса и парциальное давление кислорода, приняв за базовые значения данных параметров 225°С и 7,3 бара соответственно. Общий расход потребляемого в каждом из опытов кислорода, продолжительность опыта, а также итоговое извлечение золота из окисленного материла приведены в таблице 2. Рассматривая результаты можно с уверенностью сказать, что снижение окислительных условий сказывается в первую очередь на продолжительности опыта. Поскольку опыт проводился до полного поглощения количества кислорода, необходимого для окисления содержащихся в материале пирита и арсенопирита, то полученное путем последующего цианирования окисленного материала извлечение золота не сильно различается. Оценить динамику окисления возможно по полученным кривым поглощения кислорода, приведенным на рисунке 1.

Таблица 2 – Серия проведённых опытов по исследованию кинетики автоклавного окислительного процесса

Рис. 1 – Кривые расхода кислорода полученные в ходе проведения кинетических опытов

3. Модель автоклавного окислительного процесса

Математическое описание процесса растворения FeS и FeAs. В основу математической модели автоклавного окисления положены идей изложенные авторами и реализованные ранее в общеизвестной модели сжимающегося ядра (Shrinking Core Model, Yagi и Kunii 1995, 1961) [1]. Рассматривая количество окисляемого материала (пирита или арсенопирита) как совокупность однородных сферических частиц уменьшающегося по мере окисления радиуса (а значит и поверхности на которой проходит окисление) выделим основные стадии протекания процесса: 1) растворение газообразного кислорода и его диффузия к поверхности окисляемого материала; 2) участие кислорода в окислении, протекающим на поверхности материала, согласно реакциям (1) и (2); 3) окисление ионов Fe²⁺ до ионов Fe³⁺ в жидкой фазе под действием кислорода, согласно реакции (3).

За лимитирующую стадию процесса окисления примем стадию химической реакции, протекающей на поверхности окисляемого материала, с тем допущением, что процесс протекает в относительно идеальных гидродинамические условиях и скорость диспергации и растворения кислорода сравнительно выше скорости окисления. Концентрация насыщения кислорода в объеме растворителя (моль O₂ на кг раствора) постоянна и определяется как зависимость от парциального давления кислорода и температуры процесса, согласно предложенной Tromans модели [2]:

(4)

Принимая постоянство «концентрации пирита/арсенопирита» на поверхности твердых частиц свойством рассматриваемого материала определим степень растворения окисляемого материала через процесс постепенного сокращения как объема каждой частицы, так и реакционно активной поверхности материала:

 (5)

 (6)

где  – исходная площадь поверхности окисляемого материала, м²;  – текущая площадь поверхности частицы, м²;  – степень конверсии материала.

Поскольку лимитирующая стадия процесса – скорость поверхностной реакции окисления, то скорость поглощения кислорода определяется главным образом скоростью протекания реакции окисления на поверхности частиц пирита и арсенопирита (моль FeS₂/FeAsS в минуту):

 (7)

Скорость поглощения кислорода зависит от концентрации растворенного в жидкой фазе кислорода, реакционно площади и константы скорости поверхностной химической реакции:

, где  (8)

где  – площадь реакционной поверхности, м²;  – константа скорости поверхностной реакции, 1/м²мин;  – количество растворенного в жидкой фазе кислорода, моль.

Скорость окисления пирита выразим через скорость сокращения реакционно активной поверхности окисляемого материала:

 (9)

где n – условное число сферических частиц пирита данного радиуса (определяется степенью измельчения исходного материала);  – мольная плотность пирита, моль/м³;  – объем частицы пирита, м³;  – средний радиус сферической частицы, м;  – суммарная реакционная площадь поверхности частицы, м². Используя полученные выражения (8) и (9) выразим скорость изменения суммарной поверхности пирита:

, где  (10)

И аналогично для арсенопирита:

 , где  (11)

Скорость протекания в жидкой фазе гомогенной реакции окисления ионов Fe²⁺ до ионов Fe³⁺ определим, как:

, где  (12)

Таким образом, общее количество израсходованного согласно реакциям (1), (2), (3) кислорода определяется как:

 (13)

Параметрическая идентификация и моделирование. С целью определения неизвестных параметров модели: констант скорости реакции (,,); энергии активации (,,); порядка реакции по заданным компонентам (,,) (согласно приведенным ранее уравнениям (10), (11), (12)) проведена параметрическая идентификация посредством реализованных в пакете прикладных программ MATLAB вычислительных алгоритмов. В качестве критерия рассогласования в процессе решения задачи идентификации использована сумма квадратов отклонений, адекватность модели оценивали по значению R² и величине среднеквадратичной ошибки (RMSE).

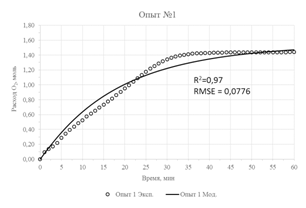
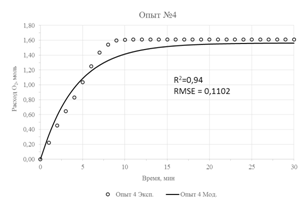
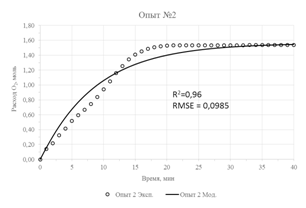
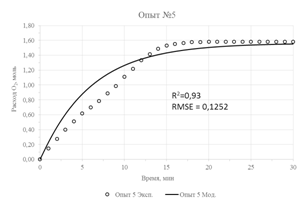
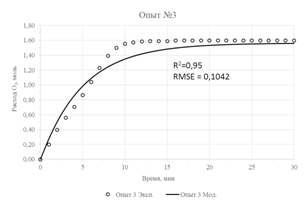
Результаты параметрической идентификации приведены в таблице 3, а результат моделирования в сравнении с исходными экспериментальными данными приведен на рисунке 2. О достаточной адекватности математической модели можно судить по значениям коэффициентов детерминации (R²), не превышающих значения в 0,93 и максимального значения стандартной ошибки, равного 0,125.

Таблица 3 – Результаты параметрической идентификации

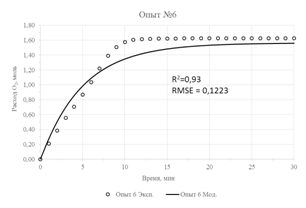Рис. 2 – Экспериментальные данные и их аппроксимация предложенной моделью

4. Выводы и заключение

1. Предложенная математическая модель автоклавного окисления сульфидных концентратов основана на описании процесса сокращения реакционно способной площади данных минералов с учетом средней крупности материала и химической активности реакционной поверхности пирита и арсенопирита.
2. Для проведения параметрической идентификации модели использованы результаты кинетических опытов окисления концентрата с содержанием FeS₂ 16,9% и FeAsS 6,9% при различных температурах и давлении. Адекватность модели оценивалась показателем R², значение которого в худшем случае было не менее 0,93.
3. В перспективе на основе полученного математического описания периодического автоклавного окислительного процесса возможно рассчитать процесса непрерывного автоклавного окисления, что полезно на стадии проектирования автоклавного участка процесса переработки золотосодержащих концентратов.

Благодарности: Работа выполнена на материальной базе ООО «Научно-исследовательский центр «Гидрометаллургия», Санкт-Петербург, Ленинский проспект 151, тел. 600-77-45, e-mail: src@gidrometall.ru

Литература

1. Levenspiel O. Chemical reaction engineering, 3^rd Edition [Текст] / O. Levenspiel. - New York: Wiley, 1999. -566 p.
2. Tromans D. Oxygen solubility modeling in inorganic solutions: concentration, temperature and pressure effect // Hydrometallurgy. 1998. Vol. 50. P. 279.