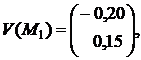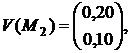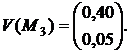ЛИНЕЙНО ИНТЕРПОЛИРОВАННОЕ ВЕКТОРНОЕ ПОЛЕ И ВЫПОЛНЕНИЕ УСЛОВИЯ СОЛЕНОИДАЛЬНОСТИ

Черёмухина Е.Е.¹, Мосин В.Г.²

¹ Магистрант первого года обучения, ² Кандидат физико-математических наук, Самарский государственный архитектурно-строительный университет

 ЛИНЕЙНО ИНТЕРПОЛИРОВАННОЕ ВЕКТОРНОЕ ПОЛЕ И ВЫПОЛНЕНИЕ УСЛОВИЯ СОЛЕНОИДАЛЬНОСТИ

Аннотация

В статье рассматривается линейная интерполяция двумерного векторного поля, которая получается по трем значениям в вершинах единичного симплекса. Построенное таким образом двумерное векторное поле расширяется до трехмерного. Указываются условия, при которых трехмерное расширение соленоидально.

Ключевые слова: линейная интерполяция, векторное поле, соленоидальность.

Cheremukhina Е.Е.¹, Mosin V.G.²

¹first-year undergraduate, ² PhD in Physics and Mathematics, assistant professor of Department of Mathematics, Samara State University of Architecture and Civil Engineering

 LINEAR INTERPOLATION OF THE VECTOR FIELD AND THE CONDITION SOLENOIDALITY

Abstract

The linear interpolation of the two-dimensional vector field. Three-dimensional expansion of the vector field. The conditions of the three-dimensional expansion of solenoidal vector field.

Keywords: linear interpolation, vector field, solenoidality.

В задачах переноса вещества векторное поле, дающее конвективную составляющую переноса, как правило, считается постоянным в области решения задачи (см., например, [1] или [2]), что не всегда согласуется с данными реальных наблюдений. В связи с этим, интересен вопрос описания произвольного поля и выяснения условий, при которых данное описание не противоречит основным законам сохранения.

В настоящей работе рассматривается линейная интерполяция векторного поля, которое задается произвольными значениями в вершинах двумерного единичного симплекса, и выводится условие, обеспечивающее его соленоидальность. Основной результат представлен в теореме 2.

1. Интерполяция двумерного векторного поля на симплексе

Пусть известны значения скалярного поля U(x,y)  в вершинах двумерного единичного симплекса S, и пусть эти значения внутри симплекса изменяются линейно. Тогда существует единственная скалярная функция u(x,y), такая что значения функции u(x,y) в вершинах симплекса совпадают со значениями скалярного поля U(x,y), и между любыми двумя точками (x₁,y₁) и (x₂,y₂) симплекса S  значение функции u(x,y) изменяется линейно.

Действительно, обозначим M_i, вершины симплекса S от начала координат  по часовой стрелке: M₁(0,0), M₂(1,0), M₃(0,1). Пусть U(M_i)=a_i. Тогда данные для скалярного поля U(x,y) — это точки M₁^'(0,0,a₁), M₂^'(1,0,a₂), M₃^'(0,1,a₃) в R³. Точки  M_i не лежат на одной прямой, следовательно, через точки M_i^'  проходит единственная плоскость, уравнение которой таково:

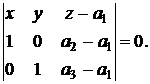(1)

Отсюда:

(2)

Понятно, что функция

(3)

является искомой.

Векторное поле V(x,y) можно рассматривать как совокупность двух скалярных полей, поэтому, полученный выше результат легко переносится на двумерный случай. А именно: для любых значений векторного поля V(x,y), вычисленных  в вершинах единичного симплекса S, существует единственная векторная функция υ(x,y)=( υ₁(x,y), υ₂(x,y)), такая что значения функции υ(x,y) в вершинах симплекса совпадают со значениями векторного поля V(x,y), и между любыми точками (x₁,y₁) и (x₂,y₂)  симплекса S значения обеих функций υ₁(x,y) и υ₂(x,y) изменяется линейно.

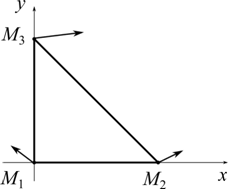(а) Заданные значения векторного поля  в вершинах двумерного единичного симплекса

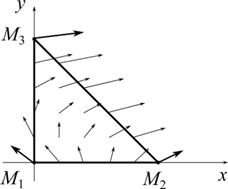(b) Интерполяция вычисленная на границах и во внутренних точках симплекса

Рис.1 Исходные данные и интерполяция векторного поля

 

Пример 1. Пусть в вершинах симплекса S наблюдаются следующие значения векторного поля V(x,y)  (см. рис. 1 (а)):

  

Применим дважды формулу (3): сначала к тройке первых координат, а затем — к  тройке вторых координат. Получим следующую интерполяцию υ(x,y) векторного поля V(x,y) :

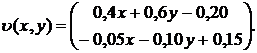(4)

Вычислим значения v(x_i,y_i), изменяя значения x и y с шагом 0,20 в пределах от 0 до 1, и получим наглядное представление о поведении векторного поля υ(x,y) (см. рис. 1(b)).

 

2. Псевдотрехмерное векторное поле на призме

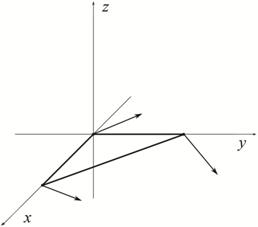
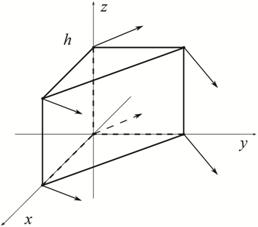
Рассмотрим прямую призму P высоты h, построенную на симплексе S. Будем считать, что при наборе высоты от 0 до h направление ветра не изменяется, и векторное поле V(x,y,z) не зависит от z (см. рис. 2)

(а) Заданные значения векторного поля  в вершинах двумерного единичного симплекса

(b) Интерполяция вычисленная на границах и во внутренних точках симплекса

Рис.2 Двумерное векторное поле на симплексе S и псевдотрехмерное векторное поле на призме P.

 

Теорема 1. Пусть l_i — стороны симплекса S, занумерованные от нуля по часовой стрелке: l₁=М₁М₂, l₂=М₂М₃, l₁=М₃М₁. Обозначим σ_i боковые грани призмы, построенные на сторонах l_i. Пусть векторное полеv υ(x,y) получается интерполяцией значений V(M_i) в вершинах M_i . Тогда объемы воздушных потоков, проходящих через боковые грани призмы P за единицу времени, вычисляются по следующим формулам:

	(5)
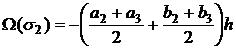	(6)
	(7)

где a_i и b_i — координаты векторов V(M_i), положительное значение Ω(σ_i) означает объем входящего потока, а отрицательное - объем исходящего.

 

Доказательство. Интерполяция векторного поля V(x,y) получается по формуле (3):

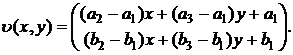(8)

Пусть υ^*(x,y,z):тривиальное трехмерное расширение двумерного векторного поля υ(x,y):

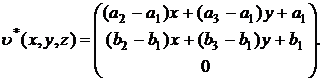(9)

Тогда

(10)

Вычислим объем потока, проходящего через грань  σ₁.

(11)

где D₁ — проекция σ₁ на плоскость xOz, и последний интеграл берется в смысле двойного интеграла. В силу того, что область D₁ является прямоугольником {0 ≤ x ≤ 1; 0 ≤ z ≤ h}, а поверхность σ_i описывается уравнением y=0, имеем:

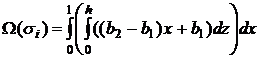(12)

Отсюда

(13)

Единичный вектор n₁ внутренней нормали к стороне l₁ симплекса S имеет координаты (0,1). Поэтому, если b₁+ b₂≥ 0, то равнодействующая векторов V(M₁) и V(M₂) образует с ним острый угол. В этом случае поток является входящим. Если же b₁+ b₂≤0, то поток является исходящим.

Вычислим объем Ω(σ₂). Воспользовавшись формулой (10), получим:

(14)

где D₁ — проекция σ₂ на плоскость xOz, D₂ — проекция σ₂ на плоскость yOz, и интегралы в правой части берутся в смысле двойных интегралов. Области D_i являются прямоугольниками {0 ≤ x ≤ 1; 0 ≤ z ≤ h}, а поверхность σ₂ описывается уравнением x+y=1. Поэтому:

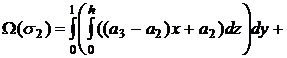
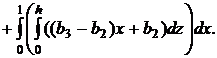(15)

Отсюда прямым вычислением получаем:

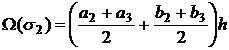(16)

Формула (16) не учитывает направление потока. Исправим это. Единичный вектор n₂ внутренней нормали к стороне l₂ симплекса S имеет координаты (‑1/√2,‑1/√2). Следовательно, если (a₂+a₃)+ (b₂+b₃) ≥0, то равнодействующая векторов V(M₂) и V(M₃) образует с n₂ тупой угол, и поток является входящим. Поэтому, для учета направления воздушного потока в формуле (16) следует изменить знак, и ее окончательный вид таков:

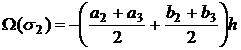
(17)

Вычисление объема Ω(σ₃) ничем не отличается от вычислений, проведенных нами выше для объема Ω(σ₁), и мы его опускаем. Теорема доказана.

Пример 2. Вернемся к примеру, где мы интерполировали векторное поле по значениям на вершинах симплекса S (см. пример 1), и вычислим объемы воздуха, проходящие через боковые грани призмы P.

Пользуясь формулами теоремы 1, имеем:

	(18)
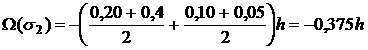	(19)
	(20)

Входящие потоки воздуха обеспечивают грани σ₁ и σ₃, а исходящий поток — грань σ₂. При этом

(21)

то есть, суммарный входящий объем на призме оказывается меньше суммарного исходящего объема, что противоречит закону сохранения массы.

3. Соленоидальное трехмерное векторное поле на призме

Теорема 1 и пример 2 показывают, что псевдотрехмерное расширение υ^*(x,y,z) двумерного векторного поля υ(x,y) не удовлетворяет условию соленоидальности, так как объем входящего потока отличается от объема исходящего.

Обозначим σ₀ нижнюю грань призмы P, и σ₄ — ее верхнюю грань. Пусть Ω(σ_i) обозначает объем воздушного потока, проходящего через σ_i за единицу времени. Тогда, в силу закона сохранения массы (см. [2], [3]), для среды с постоянной плотностью должно выполняться:

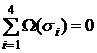(22)

Понятно, что Ω(σ₀)=0. Поэтому

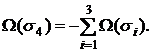(23)

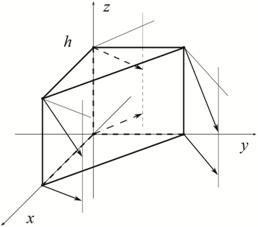
Если Ω(σ₄)≠0, то псевдотрехмерное расширение υ^*(x,y,z), введенное нами выше для двухмерного поля υ(x,y), не отвечает действительности, так как вертикальная координата трехмерного расширения поля υ(x,y) должна отличаться от нуля (см. рис. 3). Корректное трехмерное расширение двухмерного поля υ(x,y) дает следующая теорема.

Теорема 2. Пусть S — единичный симплекс, P— прямая призма высоты h, построенная на симплексе S. Пусть в вершинах M₁(0,0), M₂(1,0), M₃(0,1) симплекса S даны значения двумерного векторного поля υ(x,y)

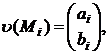(24)

а само поле υ(x,y) получается из этих значений путем линейной интерполяции за счет двукратного применения формулы (3):

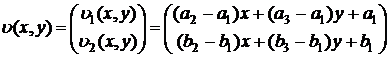(25)

 Тогда найдется единственное трехмерное векторное поле w(x,y,z) вида

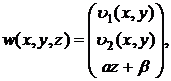(26)

которое является трехмерным расширением поля υ(x,y) и удовлетворяет условию соленоидальности (22), причем

β=0.

(27)

 

Доказательство.  Во-первых, заметим, что так как на нижней грани призмы вертикальная составляющая векторного поля w(x,y,z) должна равняться нулю, то β=0. Таким образом, будем искать w(x,y,z) в виде

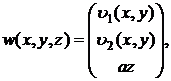(28)

Далее вычислим объем воздушного потока, который проносит поле w(x,y,z) через верхнюю грань σ₄ призмы P за единицу времени.

(29)

(а) Заданные значения векторного поля  в вершинах двумерного единичного симплекса

(b) Интерполяция вычисленная на границах и во внутренних точках симплекса

Рис.3 Псевдотрехмерное и трехмерное векторные поля на призме P.

Так как в проекции на xOy грань σ₄ дает симплекс S , а сама грань описывается уравнением z=h, то без учета знака имеем:

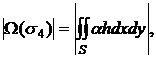(30)

где интеграл в правой части берется в смысле двойного интеграла. Нетрудно посчитать, что тогда

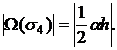(31)

Знак в формуле (31) получается следующим образом. Если α≥0, то вертикальная составляющая потока неотрицательна, и поток является исходящим (то есть дает отрицательный объем). И наоборот, если α≤0, то вертикальная составляющая потока неположительна, и поток является входящим (и объем его положителен). Поэтому

(32)

С другой стороны, согласно (23), для выполнения условия соленоидальности объем Ω(σ₄) должен равняться сумме объемов, проходящих через боковые грани, взятой с противоположным знаком. Используя результаты теоремы 1, получим:

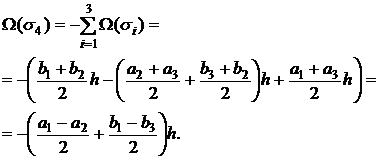(33)

Сопоставим (32) и (33):

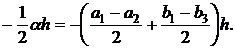(34)

откуда

(35)

Итак, трехмерное расширение w(x,y,z) двумерного векторного поля υ(x,y) найдено. Оно удовлетворяет условиям теоремы и имеет следующий вид:

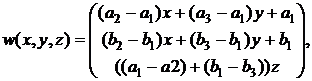(36)

Теорема доказана.

Пример 3. Выше (см. пример 1) мы интерполировали векторное поле на симплексе по его значениям в вершинах и получили (4). Теперь, пользуясь теоремой 2, имеем его трехмерное расширение на призме

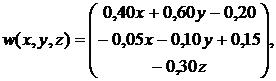(37)

причем, оно соленоидально.

Литература

1. Л. К. Мартинсон, Ю. И. Малов, Дифференциальные уравнения математической физики, Издательство МГТУ имени Н. Э. Баумана, Москва, 2006, 367 с.
2. Е. А. Власова, В. С. Зарубин, Г. Н. Кувыркин, Приближенные методв математической физики, Издательство МГТУ имени Н. Э. Баумана, Москва, 2004, 699 с.

References

1. L. K. Martinson, Ju. I. Malov, Differencial'nye uravnenija matematicheskoj fiziki, Izdatel'stvo MGTU imeni N. Je. Baumana, Moskva, 2006, 367 s.
2. E. A. Vlasova, V. S. Zarubin, G. N. Kuvyrkin, Priblizhennye metodv matematicheskoj fiziki, Izdatel'stvo MGTU imeni N. Je. Baumana, Moskva, 2004, 699 s.